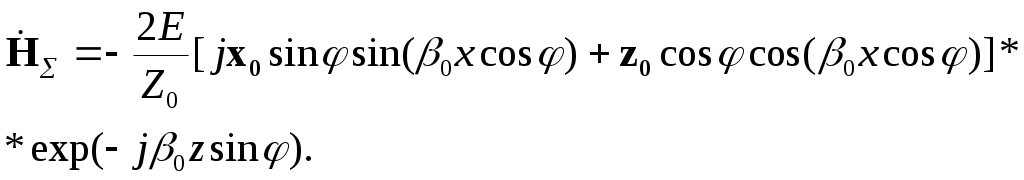Напр. направляющие. Направляемые волны и направляющие системы
 Скачать 1.44 Mb. Скачать 1.44 Mb.
|
|
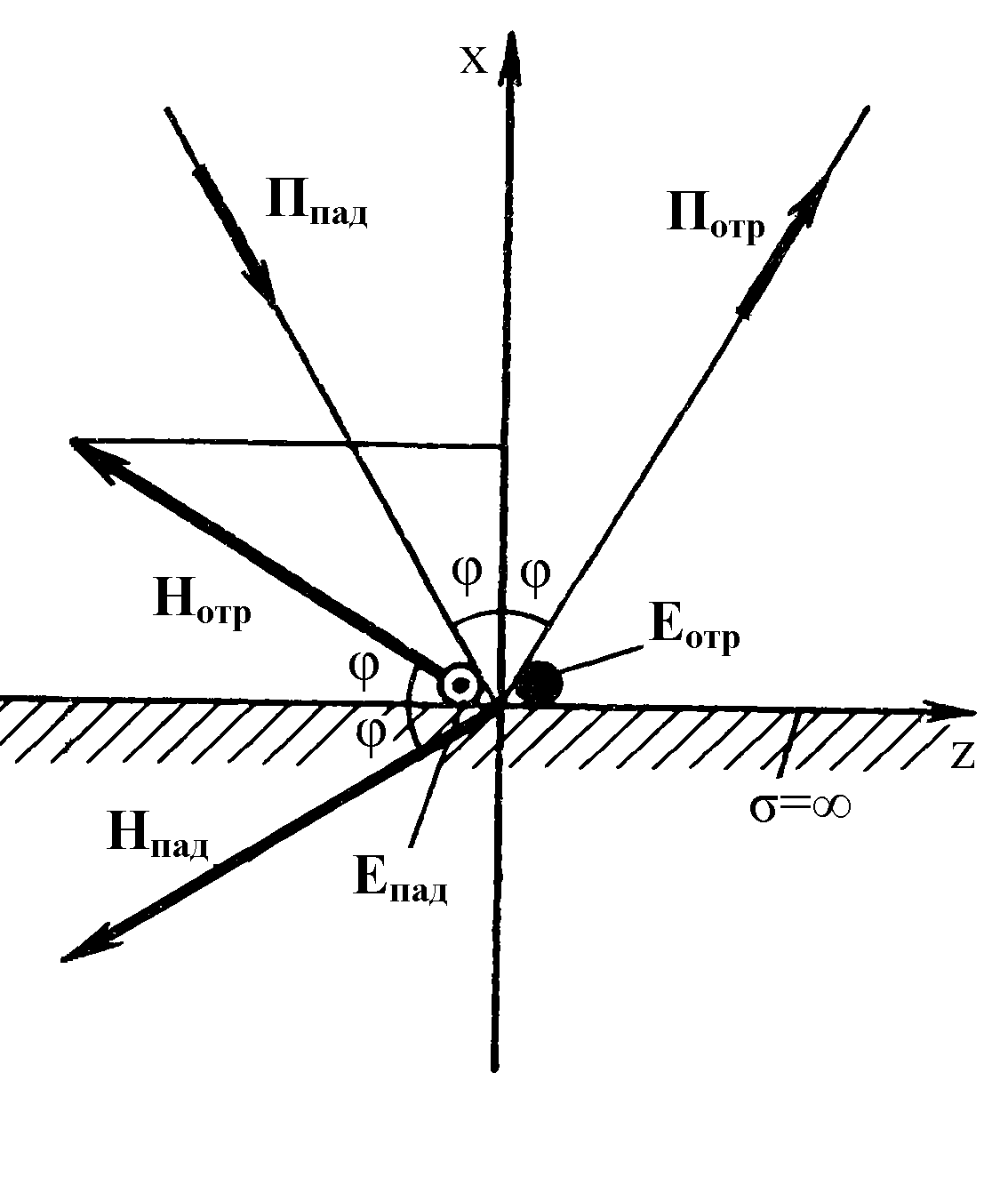
1.2. Падение волны с перпендикулярной поляризацией Чертеж, поясняющий ориентацию векторов поля в случае перпендикулярной поляризации падающей волны, приведен на рис. 1.2. Вектор напряженности электрического поля такой волны перпендикулярен плоскости падения, поэтому он параллелен отражающей плоскости и имеет единственную составляющую, направленную вдоль оси у. Вектора напряженности магнитного поля имеет две составляющие - продольную, вдоль оси z, и поперечную, вдоль оси х.
Из формул (1.8) и (1.9) следует, что при отражении перпендикулярно поляризованной волны тоже возникает неоднородная плоская волна, распространяющаяся вдоль границы раздела. В поперечном направлении поле также имеет характер стоячей волны. Принципиальное отличие этой волны состоит в том, что вектор Е имеет единственную проекцию на ось у и является чисто поперечным, а вектор напряженности магнитного поля – две: поперечную проекцию на ось х и продольную на ось z. Поэтому такая направляемая волна называется магнитной или Н-волной. Магнитной или Н-волной называется волна, у которой только вектор напряженности магнитного поля имеет продольную составляющую Н-волна возникает при падении на идеальную проводящую плоскость перпендикулярно поляризованной волны под углом менее 90˚ В этом случае поперечной волны возникнуть не может, так как при φ = 90° в нуль обращается все проекция векторов и электромагнитная волна исчезает. Таким образом, в результате отражения плоской электромагнитной волны от идеальной проводящей плоскости формируется направляемая волна, имеющая следующие характеристики. При углах падения меньше π/2: результирующее поле представляет является неоднородной продольной волной, которая распространяется вдоль отражающей плоскости; в направлении, перпендикулярном отражающей плоскости, поле имеет характер стоячей волны; при отражении волны с параллельной поляризацией формируется направляемая Е-волна, у которой только вектор напряженности электрического поля имеет продольную компоненту; при отражении волны с перпендикулярной поляризацией формируется направляемая Н-волна, у которой только вектор напряженности магнитного поля имеет продольную составляющую. При угле падения π/2 волна с параллельной поляризацией распространяется вдоль плоскости без отражения, и поле сохраняет характер поперечной или Т-волны, у которой ни один из векторов поля не имеет продольной составляющей. Волна с перпендикулярной поляризацией вдоль идеальной проводящей пластины распространяться не может. 2. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ НАПРАВЛЯЕМОЙ ЭЛЕКТРОМАГНИТНОЙ ВОЛНЫ 2.1. Структура поля волны, направляемой идеальной проводящей плоскостью Формулы (1.6) - (1.9) описывают законы изменения комплексных амплитуд векторов напряженности электрического и магнитного полей Е- и Н-волн в полупространстве над идеальной отражающей плоскостью. Зависимость проекций векторов вдоль продольной координаты z и поперечной координаты х различна. По оси z устанавливается бегущая волна так как ее фаза изменяется прямо пропорционально приращению этой координаты. По координате х поле имеет характер стоячей волны, а по координате у оно однородно. Для описания распространения волны в свободном пространстве используется волновое число γ, которое в вакууме совпадет с коэффициентом фазы β0. У направляемой волны фаза изменяется не только в направлении распространения, но и поперек его, перпендикулярно отражающей плоскости. Поэтому вводятся два волновых числа, продольное и поперечное. Способ введения их очевиден. В свободном пространстве волновое число - это коэффициент при координате в показателе степени экспоненты. Для направляемой волны аналогичный коэффициент, продольное волновое число, обозначается буквой h и описывается следующим выражением:
Продольное волновое число показывает, на сколько радиан изменится фаза волны при прохождении одного метра пути Поперечное волновое число обозначается буквой g и вводится аналогично продольному – это коэффициент при координате х:
Поперечное волновое число показывает, на сколько радиан изменится фаза волны на расстоянии 1 метр в поперечном направлении Все три волновых числа, продольное, поперечное и коэффициент фазы, связаны между собой очевидным соотношением:
Формулы (2.1) и (2.2) позволяют упростить выражения для комплексных амплитуд векторов напряженности поля над отражающей плоскостью. Так как в дальнейшем будем обсуждать только суммарное поле, нижний индекс Σ опустим. В результате получим следующие формулы. Для Е-волны:
Для H – волны:
Несмотря на существенные различия, структуры электромагнитного поля Е- и Н-волн, они имеют и общие черты. Одна из них – периодическая зависимость проекций векторов поля от продольной координаты z и поперечной координаты х. Продольной длиной волны называется пространственный период поля вдоль направления распространения Ее можно вычислить по формуле:
Из формулы (2.8) следует, что продольная длина направляемой Е- или Н-волны больше длины волны в свободном пространстве. Такие волны образуются при угле падения меньше 90˚, поэтому синус меньше единицы и длина волны увеличивается. Если угол падения равен нулю, то есть волна падает по направлению нормали, синус равен нулю и продольная длина волны становится бесконечно большой. Это означает, что на всей бесконечной отражающей плоскости колебательный процесс синфазен и ситуацию можно трактовать как бесконечно большую длину волны. При угле падения 90˚ синус равен 1 и длина направляемой волны становится равной длине волны в свободном пространстве. Но в этом случае распространяется не продольная, а поперечная, Т-волна, ее длина волны совпадает с длиной волны в свободном пространстве по определению, и в продольном волновом числе нет необходимости, так как оно равно коэффициенту фазы. Аналогично определяется поперечная длина волны. Поперечной длиной направляемой волны называется пространственный период поля по координате, перпендикулярной направляющей плоскости Поперечная длина волны рассчитывается по следующей формуле:
Отсюда следует, что поперечная длина волны больше длины волны в свободном пространстве. Она будет совпадать с длиной волны в свободном пространстве только при падении по направлению нормали, то есть под углом 0˚. Но этот случай не имеет практического смысла: волна не переносит энергии вдоль оси z, а просто существует. Поэтому можно утверждать следующее. Продольная и поперечная длины направляемых продольных волн больше длины волны в свободном пространстве У Т-волны, при φ = 900 поперечная длина волны устремляется в бесконечность, изменение напряженности поля в поперечном направлении исчезает и волна становится однородной. Чтобы наглядно представить структуру поля над отражающей плоскостью нужно на основании формул (2.4) - (2.7) построить силовые линии электрического и магнитного полей.
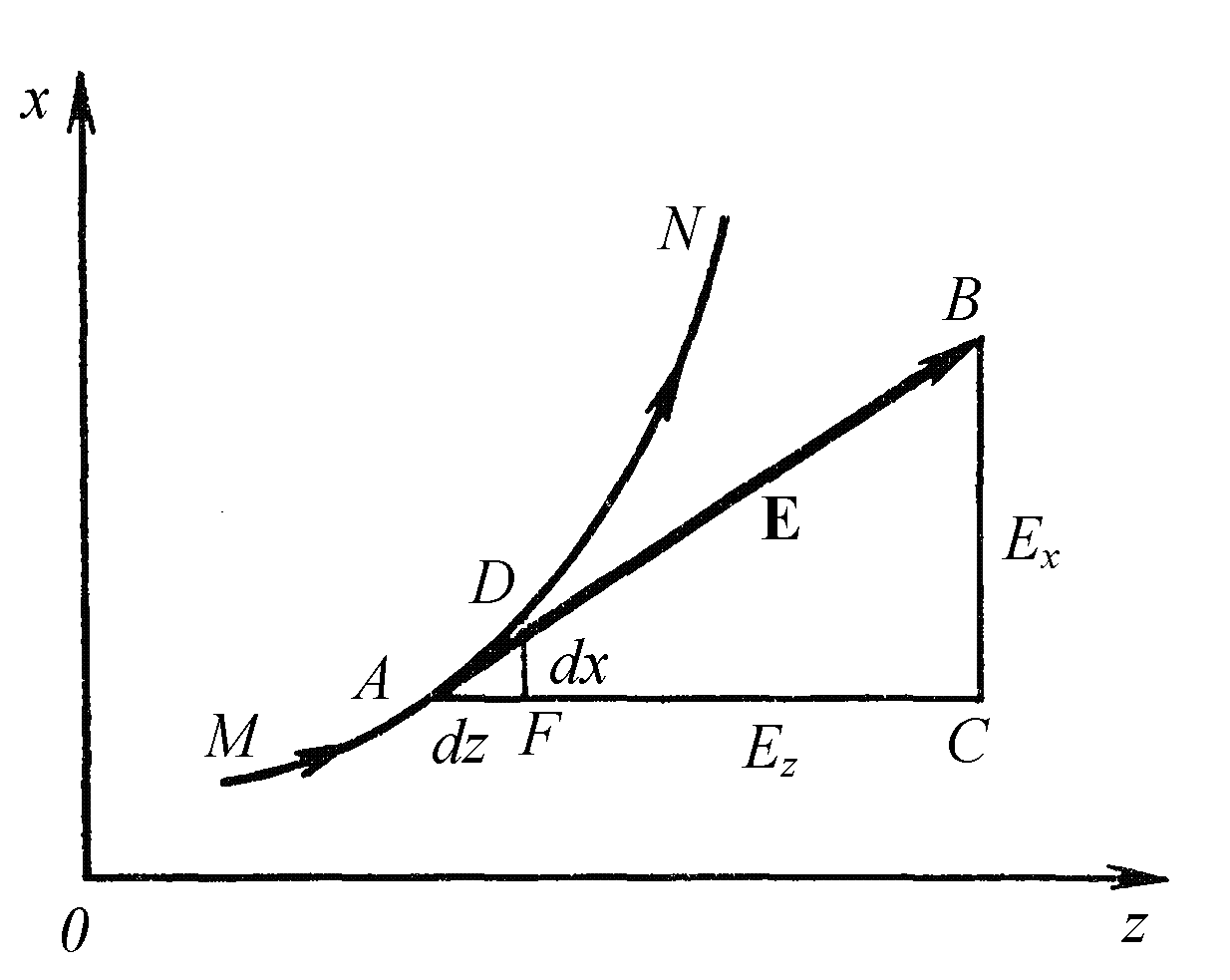
Вектор Е в точке А имеет проекции на обе оси координат. Координате z дадим приращение dz, то есть переместимся в точку D вдоль силовой линии. При этом координата х также получает приращение на величину dх. Пренебрежем малыми величинами порядка квадратов дифференциалов и заменим дифференциал дуги дифференциалом касательной. Следовательно, прямоугольный треугольник ADF можно считать подобным треугольнику ABC. Из условия подобия можно записать:
Это равенство является дифференциальным уравнением силовой линии электрического поля. Однако для ее построения поля одного уравнения недостаточно. Необходимо задать начальное условие, то есть указать точку пространства, через которую должна проходить эта силовая линия. Проиллюстрируем эту методику на примере построения силовых линий электрического поля Е-волны. Для этого опишем мгновенное11 значение вектора напряженности электрического поля, то есть умножим формулу (2.4) на ехр(jωt) и возьмем действительную часть произведения. Получим:
Силовые линии поля будем строить для момента времени t = 0. Тогда на основании выражений (2.10) и (2.11) получим следующее дифференциальное уравнение:
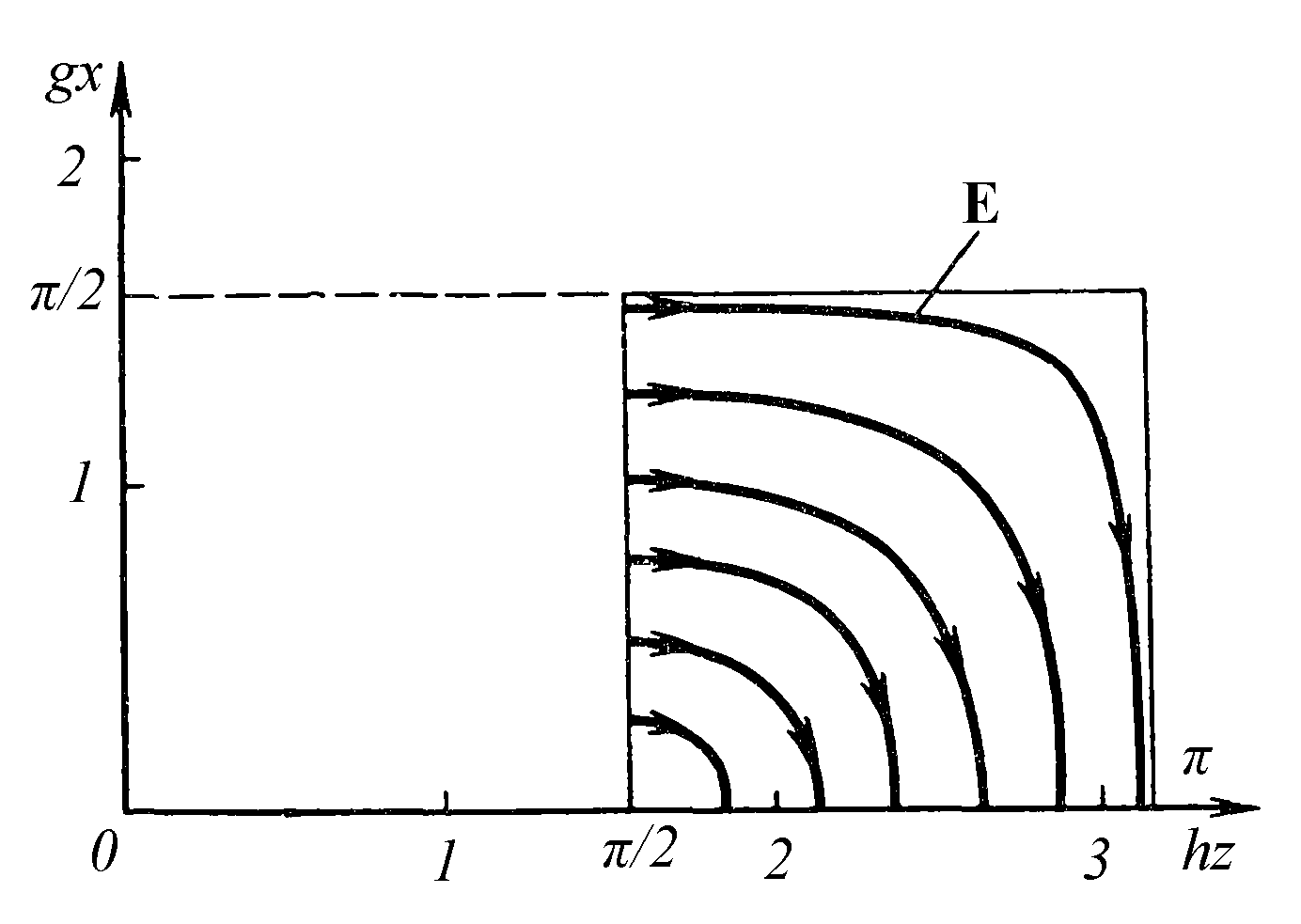
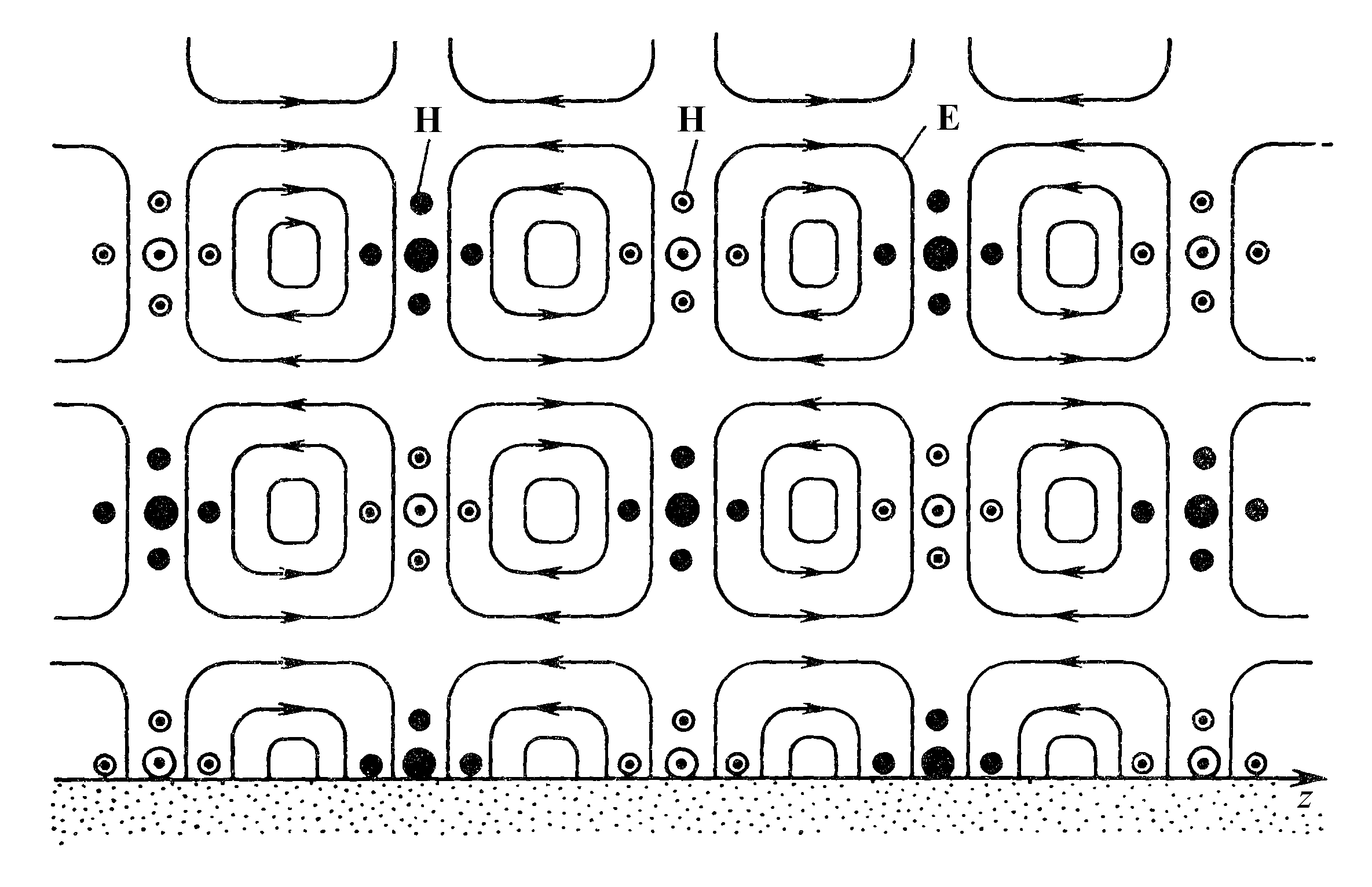
Анализ этого уравнения позволяет сделать следующие выводы. 1) На границе раздела при х = 0 производная dx/dz бесконечна. Силовые линии электрического поля подходят к поверхности идеального проводника по нормали, как и должно быть в соответствии с граничными условиями. Силовые линии электрического поля подходят к поверхности идеального проводника по направлению нормали 2) Картина силовых линий периодическая. По оси z она имеет период λпр, а по оси х - λпоп, поэтому силовые линии электрического поля Е-волны представляют собой замкнутые кривые, лежащие в плоскости xz. Исключение составляют те линии, которые «входят» в идеальный проводник или «выходят» из него. Они должны начинаться и заканчиваться на проводящей плоскости. На рис. 2.2 изображена группа кривых, построенных путем численного интегрирования уравнения (2.12) для угла падения 45°.
На рис. 2.2 приведена иллюстрация, поэтому требования к точности графического построения картины поля невысоки и дифференциальное уравнение можно решать простейшим численным способом - методом Эйлера первого порядка. Согласно этому методу исходное дифференциальное уравнение приближенно заменяют уравнением в конечных разностях:
Вычисления начинаются с некоторой начальной точки с координатами х0, z0. Затем независимой переменной z дается приращение Δz, вычисляется приращение Δx, и определяются координаты очередной точки x1 = x0 +Δx, z1 = z0 + Δz . Эту операцию циклически повторяют с фиксированным приращением Δz до тех пор, пока текущие координаты не достигнут границ области. Силовые линии на рис. 2.2 построены для шести начальных точек, у которых фаза продольной волны одна и та же, π/2, а фаза поперечной волны принимает значения от 0.25 до 1.5.
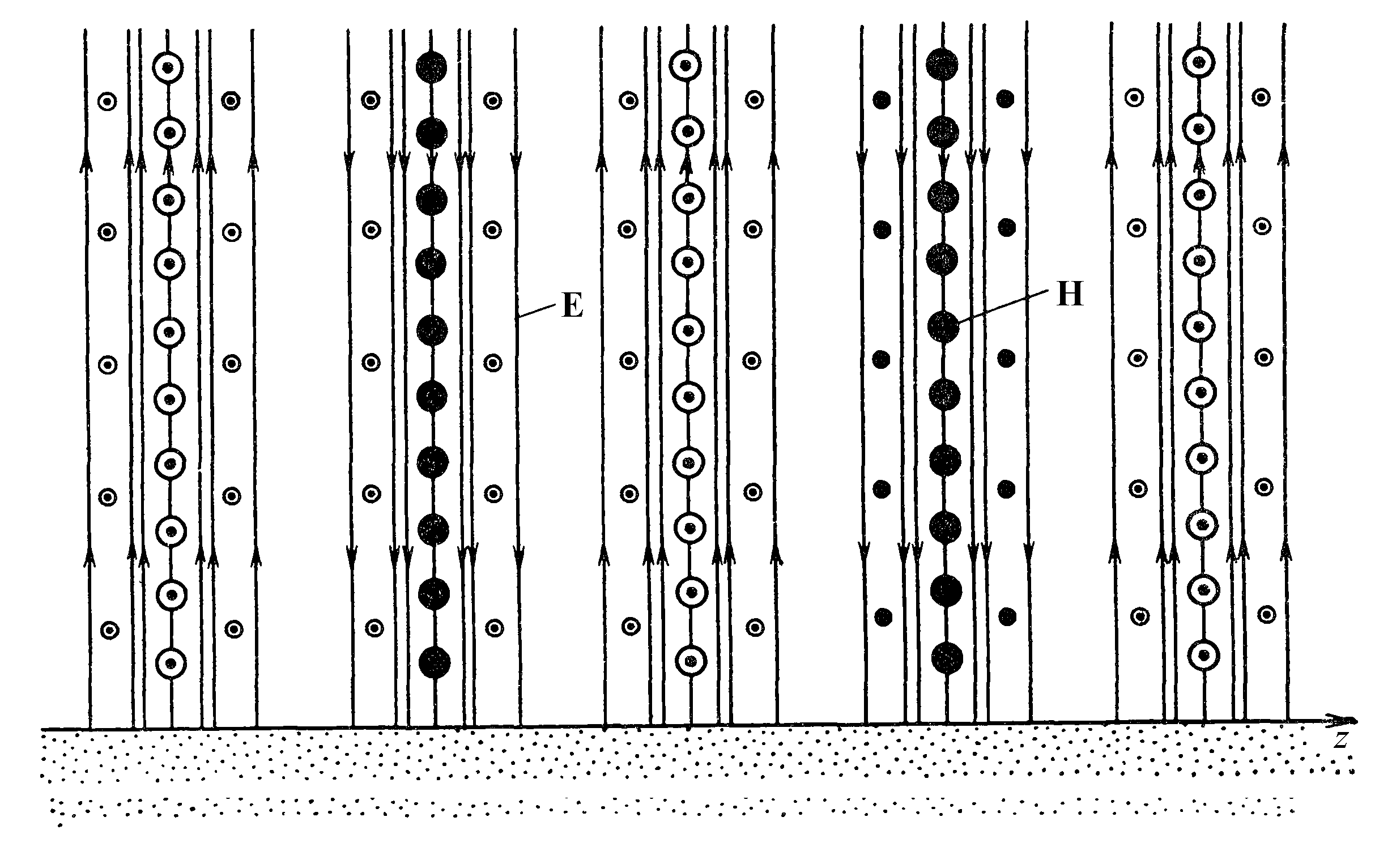
Необходимо обратить внимание на некоторые особенности распределения поля. Как и требуют граничные условия, силовые линии электрического поля подходят к отражающей поверхности по направлению нормали. Кроме того, стрелки на соседних кривых направлены в разные стороны. Так получается потому, что каждая группа кривых соответствует одной половине длины волны. Значит, в местах построения двух соседних групп кривых векторы напряженности электрического поля направлены противоположно. Это легко понять, если вспомнить график синусоиды, на котором соседние полуволны расположены по разные стороны оси координат и значения функции имеют разные знаки. Здесь происходит то же самое. По поперечной координате х, перпендикулярной отражающей плоскости, структура поля аналогична. На этом же рисунке построены силовые линии магнитного поля, которые параллельны оси у. Направление вектора напряженности магнитного поля также периодически изменяется. Вектор, направленный от нас, обозначен сплошным кружком, а направленный к нам - кружком с точкой. Диаметр кружка пропорционален величине напряженности магнитного поля. Магнитное поле Е-волны концентрируется в тех областях пространства, где велика поперечная проекция напряженности электрического поля. Это происходит потому, что коэффициент пропорциональности между векторами Е и Н, волновое сопротивление, в вакууме - действительная величина. Поэтому сдвига фаз между электрическим и магнитным полем нет, и положения максимумов их поперечных составляющих совпадают. Направляемая Е-волна возникает, если падающая волна поляризована параллельно и падает под углом менее 90˚. При угле падения этой волны 90˚ возникнет направляемая поперечная волна (Т-волна). Она распространяется вдоль идеальной проводящей плоскости без отражения. Значит, поперечное волновое число равно нулю, а продольное совпадает с коэффициентом фазы волны в вакууме. Проекции комплексных амплитуд векторов электромагнитного поля прямо вытекают из формул (2.4) и (2.5), в которых следует опустить коэффициент 2, так как отраженная волна отсутствует. В результате получим:
На основании этих формул можно записать выражения для мгновенных значений векторов напряженности поля в момент времени t = 0:
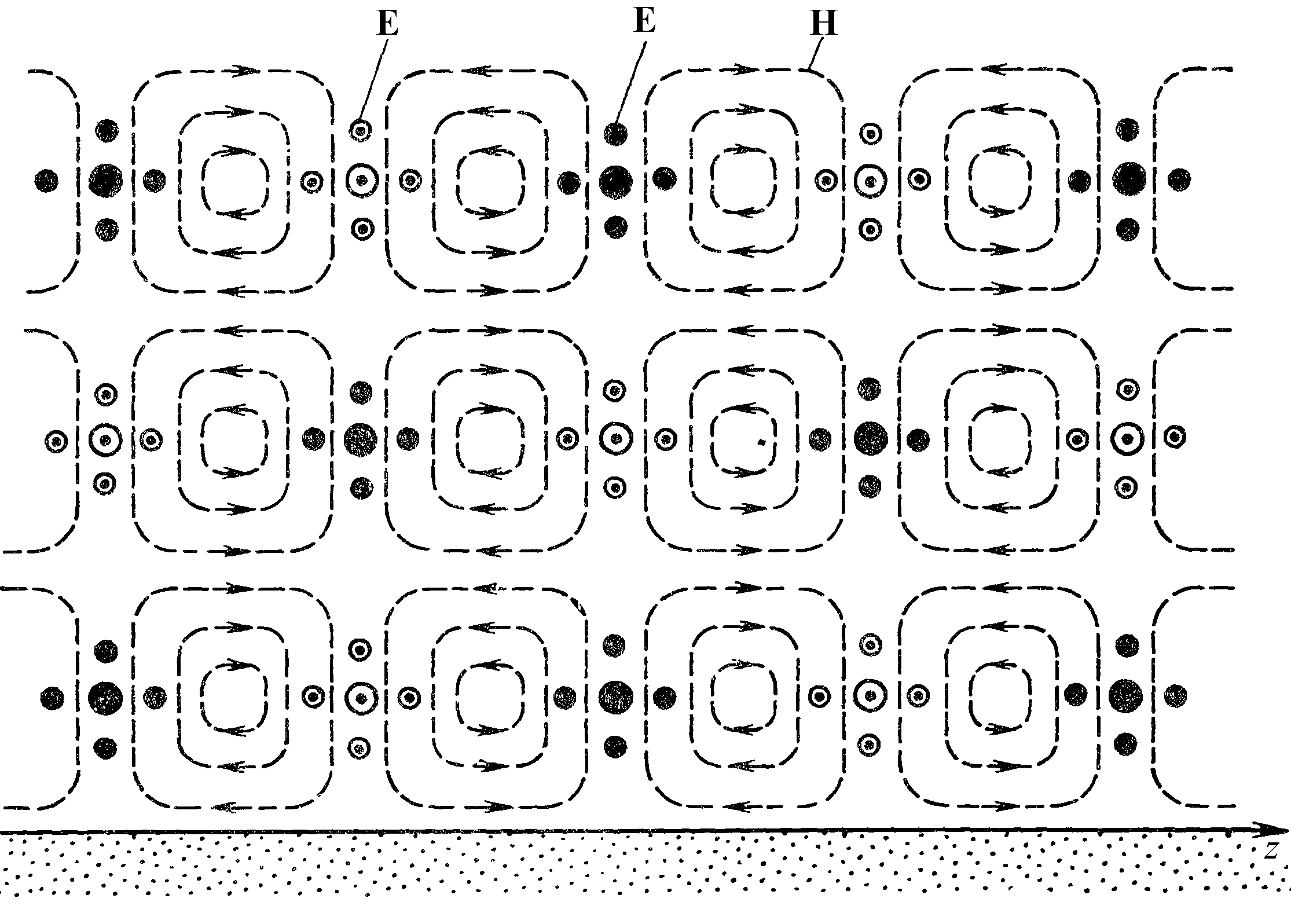
На отражающей плоскости нормальная составляющая вектора Н и тангенциальная составляющая вектора Е обращаются в нуль. Это соответствует граничным условиям на поверхности идеального проводника. В остальном картины полей Е- и Н-волн одинаковы с точностью до перестановки векторов Е и Н. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||