Напр. направляющие. Направляемые волны и направляющие системы
 Скачать 1.44 Mb. Скачать 1.44 Mb.
|
|
2.2. Плотность поверхностного тока на направляющей плоскости На идеальной проводящей плоскости в электромагнитном поле возникнет ток. Так как электропроводность плоскости бесконечна, этот ток будет поверхностным. Знание картины распределения поверхностного тока необходимо для анализа работы и конструирования реальных металлических волноводов. Поверхностный ток на идеальной отражающей плоскости численно равен модулю проекции вектора Н на эту плоскость и направлен перпендикулярно ей. В Е-волне вектор напряженности магнитного поля направлен вдоль оси у, значит, поверхностный ток будет протекать вдоль оси z. С учетом этого получим:
Эта формула описывает бегущую волну тока, вектор которого ориентирован вдоль направления распространения волны, оси z. Поверхностный ток, создаваемый Е-волной, ориентирован вдоль направления распространения волны Распределение вектора плотности тока, создаваемого Е-волной, имеет следующие особенности. Во-первых, ни модуль η, ни направление его протекания не зависит от координаты у потому, что электромагнитное поле от нее не зависит. Во-вторых, в направлении распространения волны, то есть вдоль оси z, поле имеет периодическую структуру. В одной половине длины волны ток течет в положительном направлении оси z, а в другой – наоборот, что соответствует полуволнам магнитного поля. Между любыми двумя соседними полуволнами, вдоль оси у, имеется линия, на которой модуль вектора плотности поверхностного тока равен нулю. Необходимо помнить, что это распределение движется в направлении распространения волны. Иной будет структура поверхностного тока Н-волны. В этом случае на границе раздела вектор Н имеет единственную составляющую, направленную вдоль оси z и поверхностный ток будет ориентирован перпендикулярно этой оси. Значит, выражение для комплексной амплитуды вектора плотности поверхностного тока примет вид:
Так же, как и в Е-волне, направление тока меняется на противоположное с шагом в половину длины волны. Однако в Н-волне поверхностный ток протекает не в продольном, а в поперечном направлении. Поверхностный ток, создаваемый Н-волной, ориентирован поперек направления распространения волны Эти результаты позволяют при заранее известной поляризации падающей волны заменить сплошной металлический отражатель системой параллельных проводящих стержней, пластин, проволок и т. д. Эти проводники должны размещаться с шагом 0,1λ или чаще, и быть ориентированными вдоль линий поверхностного тока. Тогда плоскость и ряд параллельных проволок будут работать примерно одинаково. Если же стержни разместить перпендикулярно линиям тока, они работать не будут, и направляемая волна перестанет существовать. 2.3. Фазовая скорость волн Фазовая скорость электромагнитной волны равна отношению круговой частоты к коэффициенту фазы. Ранее мы установили, что продольное волновое число направляемой волны является аналогом коэффициента фазы волны в безграничном пространстве. Это позволяет описать фазовую скорость направляемой волны в вакууме над абсолютно проводящей пластиной следующей формулой:
В знаменателе стоит синус, значит, что при любом угле падения меньше 90° фазовая скорость направляемой волны больше скорости света в вакууме. Отсюда следует фундаментальное свойство продольных волн, направляемых проводящей плоскостью. Фазовая скорость продольных волн, направляемых проводящей плоскостью, больше фазовой скорости волн в свободном пространстве Поэтому Е- и Н-волны, возникающие при отражении от проводящей плоскости называют быстрыми волнами.
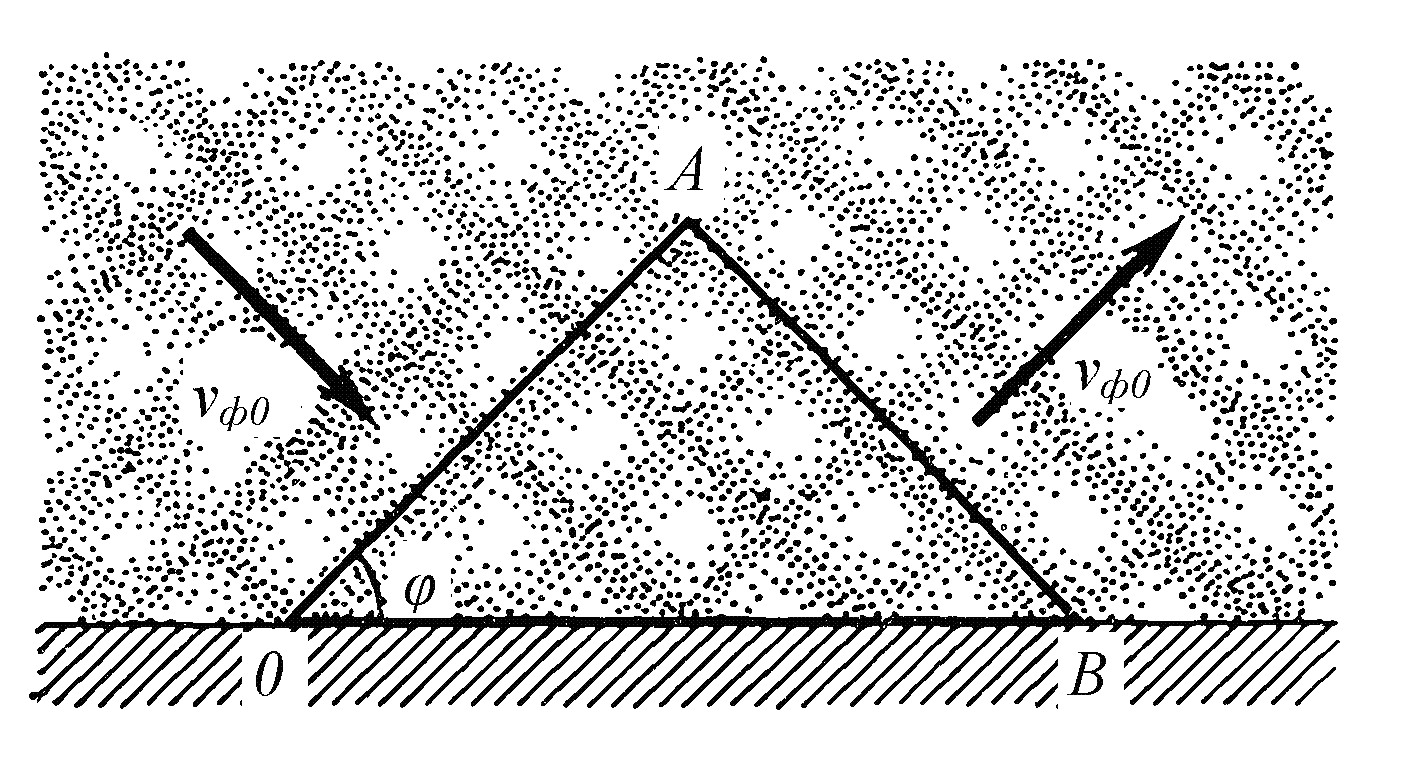
Обозначенная на рис. фазовая скорость волны vф0 – это скорость в свободном пространстве. Нас же интересует скорость перемещения фронта волны вдоль направляющей плоскости. Волна падает на плоскость под углом φ. Для определения скорости ее перемещения вдоль плоскости, выделим треугольник ОАВ, и зафиксируем в нем точку В. При этом точка А будет перемешаться к ней с фазовой скоростью: расстояние АВ будет уменьшаться по следующему закону:
Фронт падающей волны пересекается с отражающей плоскостью в точке О. Определим скорость перемещения этой точки вдоль отражающей плоскости. Точки А и О принадлежат одному фронту, значит, они должны прийти в точку В одновременно. Но расстояние АВ – это катет, а расстояние ОВ – гипотенуза, то есть расстояние ОВ больше. Для одновременного прихода точек А и О в точку В скорость движения точки О вдоль плоскости должна быть больше скорости движения точки А. Рассмотрев рис. 2.6, легко получить следующее соотношение:
Этот результат соответствует формуле (2.18). Из формулы (2.18) следует, что фазовая скорость продольных волн больше скорости света. Но согласно постулату Эйнштейна скорость света является максимальной скоростью переноса энергии или материи. Здесь нет противоречия, так как фазовая скорость является скоростью движения некоторой условной поверхности, волнового фронта. Это не энергия и не материя, на скорость ее движения ограничение Эйнштейна не распространяется. Если волна падает по направлению нормали, т.е. φ = 0, фаза колебания во всех точках отражающей плоскости будет одинаковой. В этом случае формально можно считать фазовую скорость волны вдоль оси z бесконечной. В другом предельном случае, при φ = 90˚, волна будет распространяться вдоль плоскости без отражения и ее фазовая скорость будет равна скорости в свободном пространстве. Этот случай возможен только при параллельной поляризации падающей волны. В результате получается направляемая поперечная или Т-волна. Фазовая скорость Т-волны, направляемой проводящей плоскостью, равна фазовой скорости в свободном пространстве Таким образом, мы выяснили, что фазовая скорость волн, направляемых проводящей плоскостью, не меньше скорости волн в свободном пространстве. 2.4. Связь между продольными и поперечными составляющими векторов напряженности поля направляемой волны Идеальная отражающая плоскость является простейшей направляющей системой. Очевидно, что практического значения она не имеет, однако Е- и Н-волны, возникающие в полупространстве над ней, являются моделями электромагнитных волн в реальных полых металлических волноводах. Значит, имеет смысл в этом простейшем случае определить общие свойства направляемых волн. Эта возможность обусловлена тем, что продольная направляемая волна является неоднородной волной, распространяющейся вдоль оси z. Комплексную амплитуду каждой проекции векторов этой волны на оси координат можно описать следующей формулой:
Значит, изменение поля вдоль направления распространения и в поперечной плоскости можно описать отдельно. Применим эту возможность к электромагнитному полю в области пространства без источников, которое описывается первыми уравнениями Максвелла для комплексных амплитуд:
Эти уравнения надо расписать в координатной форме. Получим:
Далее надо вычислить производные по координате z от проекций векторов поля с помощью очевидной формулы:
С учетом этого уравнения (2.24) – (2.29) упростятся:
В уравнениях (2.31) – (2.36) поперечные составляющие векторов Е и Н являются линейными комбинациями из производных от продольных проекций этих векторов по поперечным координатам х и у. После некоторых преобразований легко получить следующую группу формул:
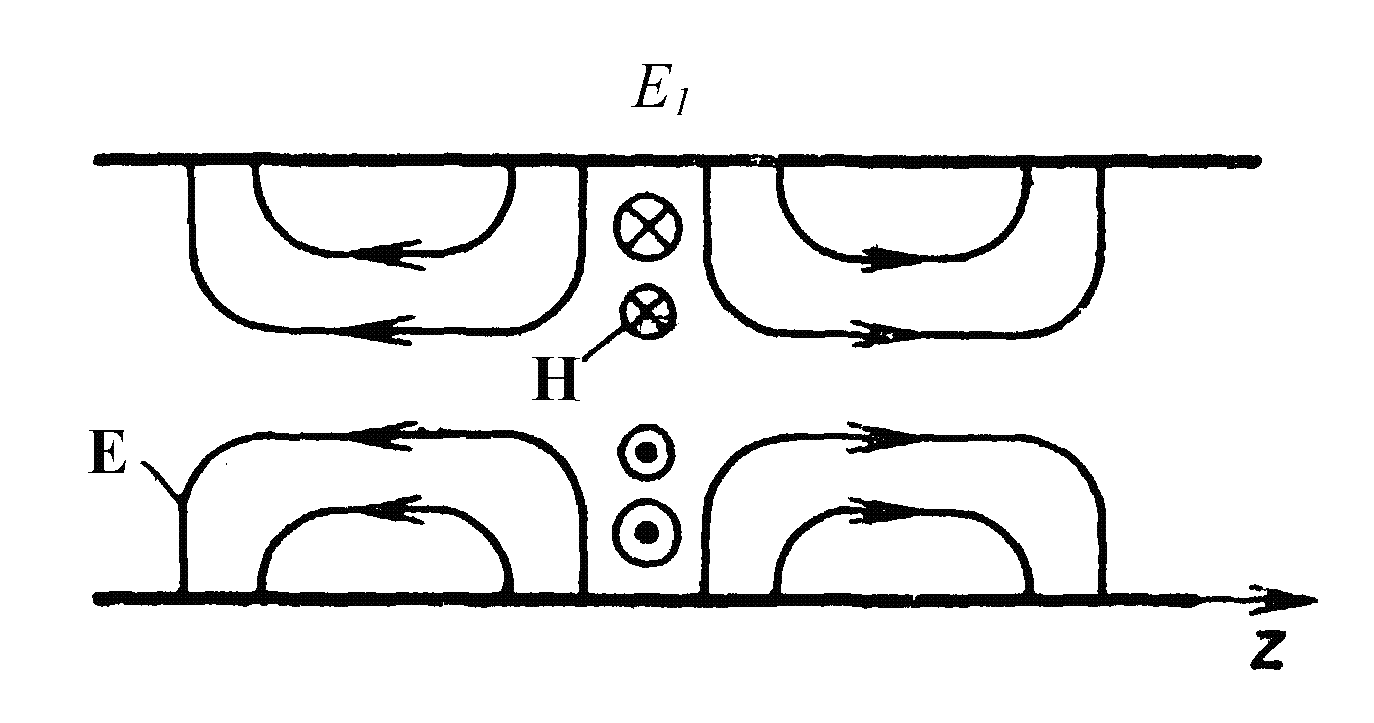
Равенства (2.37) – (2.40) являются формулами перехода от продольных составляющих векторов напряженности поля направляемой электромагнитной волны к поперечным. Их использование позволяют упростить решение уравнений распространения волн в волноводах: достаточно найти всего две функции, описывающие зависимость продольных составляющих поля волны от поперечных координат. Поперечные составляющие поля определяются простым дифференцированием продольных компонент векторов напряженности поля. 3. ПЛОСКИЙ ВОЛНОВОД Мы установили, что проводящая плоскость обладает способностью направлять электромагнитные волны. При этом электромагнитная энергия распространяется только в половине пространства, отделенной плоскостью. По сравнению с распространением в свободном пространстве степень концентрации энергии увеличилась вдвое, но осталась бесконечно малой: полупространство вдвое меньше безграничного пространства, однако бесконечно велико. Для увеличения степени концентрации энергии электромагнитного поля можно на некотором расстоянии от первой идеальной проводящей плоскости установить параллельно ей вторую такую же плоскость. Это приведет к тому, что волны будут распространяться лишь в промежутке между двумя плоскостями. Такая направляющая система называется плоским волноводом. Плоским волноводом называется направляющая система, состоящая из двух параллельных идеальных проводящих плоскостей Так как плоскости бесконечны, единственной геометрической характеристикой плоского волновода является расстояние между ними, поэтому необходимо разобраться, каким должно быть это расстояние для того, чтобы волна распространялась. Для этого обратимся к рис. 2.3, на котором изображена структура поля направляемой Е-волны. Кривые на рис. – это силовые линии электрического поля. На направляющей плоскости выполняется условие равенства нулю тангенциальной компоненты вектора напряженности электрического поля, поэтому силовые линии подходят к ней по нормали. Вторую плоскость надо расположить на таком расстоянии, чтобы и на ней это граничное условие выполнялось.
Силовые линии электрического поля лежат в плоскости рис., а силовые линии магнитного поля ему перпендикулярны. В продольном направлении структура поля имеет периодический характер и в соседних половинах длин волн силовые линии направлены в противоположные стороны. Волна, структура поля которой изображенная на рис. 3.1, обозначена Е1. Буква Е означает, что направляемая волна электрическая, то есть продольную компоненту имеет только вектор напряженности электрического поля. Нижний индекс 1 говорит о том, что между стенками плоского волновода укладывается одна полуволна стоячей волны. Теперь вернемся к рис. 2.3. Обратите внимание на структуру поля над отражающей пластиной. Очевидно, что граничное условие можно выполнить не только на расстоянии в половину длины волны, но и на больших расстояниях, однако всегда расстояние между плоскостями должно быть кратно половине длины волны. При этом коэффициент кратности может быть любым числом, но обязательно целым. Поле магнитной волны над отражающей плоскостью изображено на рис. 2.5. В плоскости рис. лежат силовые линии магнитного поля, а силовые линии поля электрического ей перпендикулярны. Картина поля также периодическая с шагом в половину длины волны. Это позволяет утверждать, что все сказанное об электрической волне действительно и для магнитной.
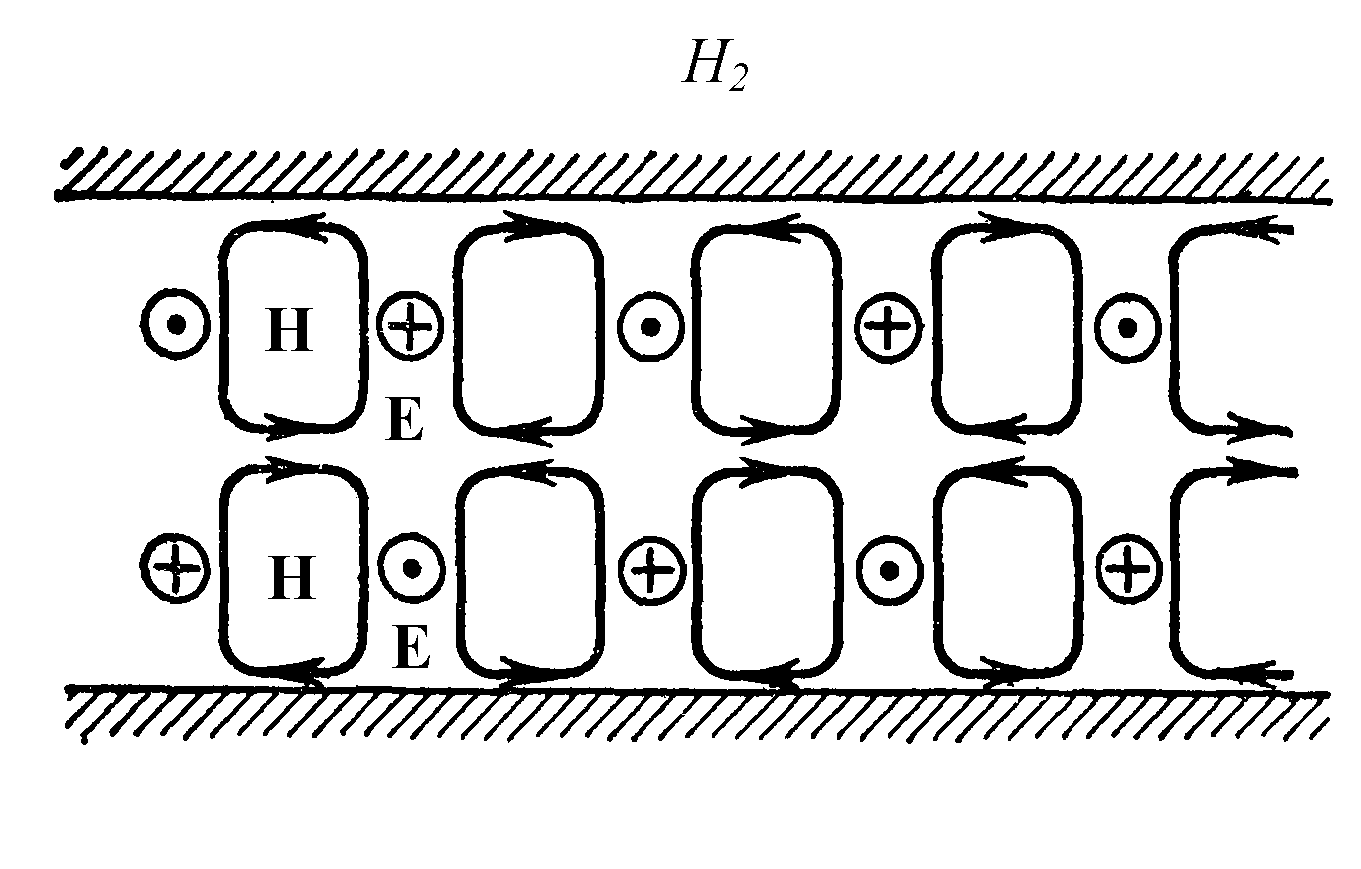
Эта волна обозначена Н2. Буква Н говорит о том, что волна магнитная, а нижний цифровой индекс - о количестве полуволн между плоскостями волновода. Их две. Эти примеры поясняют обозначение волн в плоском волноводе. Оно состоит из буквы и нижнего числового индекса. Буква Е соответствует электрической волне, а буква Н – магнитной. Если в плоском волноводе распространяется поперечная волна, она обозначается буквой Т. Нижний числовой индекс указывает количество полуволн стоячей волны, укладывающихся в промежутке между плоскостями волновода. Он есть только у Е- и Н-волн. У Т-волны числового индекса нет, так как поле между пластинами однородно. Различные виды волн в волноводах называются модами. Разные виды волн в волноводах называются модами В некоторых учебниках вместо термина «мода» используется термин «тип», который означает то же самое – разновидность волны в волноводе. Направляемые волны в плоском волноводе классифицируются по продольной составляющей вектора напряженности поля и по количеству полуволн стоячей волны между плоскостями Эти три вида волн, Е-, Н- и Т-волны, охватывают все случаи распространения в наиболее часто встречающихся волноводах. Но в некоторых волноводах могут распространяться волны, у которых продольную составляющую имеют оба вектора напряженности поля. Такие волны называются гибридными. Гибридными называются волны, у которых оба вектора напряженности поля имеют продольные составляющие Осталось рассмотреть Т-волну, поле которой изображено на рис. 2.4. Структура поля по поперечной координате х постоянна и вектор напряженности электрического поля перпендикулярен направляющей плоскости. Это говорит о том, что вторую плоскость можно расположить на любом расстоянии от первой. Граничное условие будет выполняться всегда, поэтому направляемая Т-волна не имеет нижнего числового индекса. |