Эксплуатация наклонно направленных насосных скважин by Уразаков. Насосных
 Скачать 1.96 Mb.
|
|
где F - геометрический коэффициент; п - число ходов в минуту; S - длина хода, м; μ - вязкость, мПа*с; L - длина подвески насоса, м. Значение коэффициента Fв функции отношения диаметра штанг к внутреннему диаметру НКТ представлено графически на рис. 24. Графическая зависимость была аппроксимирована формулой, которая позволила преобразовать расчетную зависимость (61) к виду  (62)где т =dшт/dтр; υ - скорость штанг, м/с. Формула (62) - наиболее простая зависимость для определения гидродинамического трения в подземном оборудовании. Ход вверх. Расчетные формулы для хода штанг вверх имеют более сложный вид, поскольку в зависимости от диаметра плунжера насоса меняется характер приложения гидродинамической нагрузки штанговой колонне. При малых диаметрах плунжера нагрузка трения рассредоточена по длине штанговой колонны. При больших поперечных размерах насоса нагрузка вязкого трения приложена к торцу плунжера, причем в области средних значений диаметров плунжера нагрузка трения минимальная. Для области малых диаметров плунжера выражение для нагрузки можно записать в следующем виде [14]:  (63)Соответственно для области больших размеров  (64) Коэффициенты c1, входящие в формулы для определения N1и M1, приведены в табл. 8. Границы применимости формул (63) и (64) определяются выражениями  ,  При DH <  для расчета нагрузок трения применяется формула (63), а при DH > - формула (64). В интервале значений диаметра плунжера DH ≈ формула для определения нагрузки трения имеет вид 2.11. РАСЧЕТ НАГРУЗОК НА ГОЛОВКУ БАЛАНСИРА Для определения нагрузки на головку балансира используется проекция на ось скважины уравнения равновесия колонны штанг, которое запишем в виде  (65)Начальное условие Т(0) = Рпли силы сопротивления FTи Fμ зависят, вообще говоря, от самого продольного усилия T(S) в направлении движения штанг. Зависимость FТот продольного усилия определена с учетом искривления скважины с помощью проекции уравнений равновесия колонны в нормальном к оси скважины направлении. Из выражения (47) имеем  (66), (67), (68)При определении Fи Рплприняты некоторые постоянные значения эксцентриситета колонны штанг в НКТ, и поэтому здесь Fи Рпл зависят не от продольного усилия, а лишь от направления движения колонны. Обычно частота качаний станка-качалки гораздо меньше, чем частота собственных упругих колебаний колонны штанг. При этом рассматриваемое квазистатическое равновесие колонны соответствует усреднению за период времени больший, чем период собственных колебаний колонны [11]. В течение рабочего цикла насоса полированный шток дважды (в верхнем и нижнем положении) останавливается. Если бы колонна не растягивалась, то в эти моменты она бы тоже вся останавливалась. Поскольку коэффициент трения при нулевой скорости достигает локального минимума (трение покоя), то и нагрузки трения были бы наибольшими. Однако в действительности часть колонны вследствие инерции и упругих перемещений продолжает двигаться, и поэтому трение не достигает экстремальных значений. Кроме того, вблизи моментов остановок штока меняются режим работы клапанов насоса и, следовательно, нагрузки на плунжер. Поэтому в эти моменты общие нагрузки на балансир также не достигают экстремума. Когда полированный шток располагается вблизи среднего положения, клапаны насоса находятся в одном состоянии и нагрузки от веса и трения жидкости не изменяются. В эти отрезки времени колонна движется практически с одной скоростью, и для определения сил граничного трения можно считать скорость постоянной. Далее будем рассчитывать нагрузки в предположении постоянной вдоль колонны скорости, равной максимальной скорости движения полированного штока. 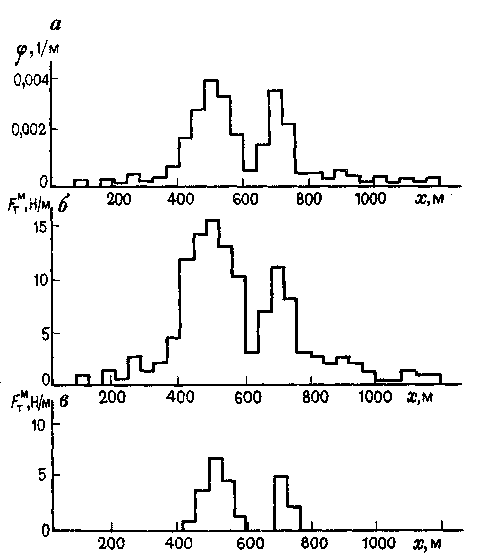 Рис. 25. Изменение прижимающей силы и кривизны оси ствола скважины по глубине: а - кривизна; б -прижимающая сила муфт; в - прижимающая сила тела штанг Для расчетов по изложенной методике с помощью ЭВМ во ВНИИ составлена программа INCL. Программа позволяет определить нагрузку на головке балансира при ходе штанг вверх и вниз, а также при ходе вниз с незаполнением насоса. Кроме того, на всем протяжении колонны рассчитывают прижимающую силу и силу граничного трения муфт и штанг о насосные трубы. Дифференциальные выражения для характеристик профиля скважины представляют с помощью конечных разностей, интегрирование уравнения равновесия производят с помощью метода Эйлера. Программа позволяет рассчитывать одно-, двух- и трехступенчатую колонну. Здесь приводятся результаты расчета для штанговой установки в скв. 548 Сергеевского месторождения в Башкирии. Инклинометрические измерения использованы через 40 м. Колонна составлена из штанг диаметром 19 мм и 22 мм в количестве соответственно 88 и 62. Длина штанги с муфтой 7,8 м. Длина колонны L - 1170 м, глубина подвески Н = 1140 м. Нагрузка от веса колонны составляет Рвш= 30,03 кН. Диаметр насосных труб и плунжера равен соответственно 62 и 43 мм. Максимальная скорость движения колонны 0,437 м/с. Вязкость продукции скважины 1,6 мПа*с. На рис. 25 показаны кривизна оси скважины и силы граничного трения при ходе колонны вверх в зависимости от Таблица 9 Результаты замеров и расчета усилий на штанговую колонну
|