натуральные числа. Натуральных числа и их свойства. Натуральных числа и их свойства, метод математической индукции методика их изучения
 Скачать 2.76 Mb. Скачать 2.76 Mb.
|
|
Натуральных числа и их свойства, метод математической индукции; методика их изучения. Понятие натурального числа является исходным понятием арифметики. Аксиомы натуральных чисел были сформулированы итальянским математиком Д. Пеано: 1. Для каждого натурального числа n существует только одно, следующее за ним натуральное число, обозначаемое n'. 2. Единица, обозначаемая 1, является натуральным числом, причем она не следует ни за каким натуральным числом. 3. Ни одно натуральное число не следует за двумя различными натуральными числами. 4. Если множество A содержит единицу и вместе с каждым числом n содержит следующее за ним натуральное число n', то A содержит все натуральные числа. Используя эти аксиомы, для натуральных чисел определяются операции сложения, умножения, деления, отношение порядка и др. В частности, по определению полагается n + 1 = n’. Четвертую аксиому Пеано называют аксиомой математической индукции и именно на ней основан метод математической индукции, состоящий в следующем.   Методика изучения натуральных чисел В математике имеются различные теории построения каждого множества чисел. Для построения арифметики натуральных чисел используется обычно аксиоматический подход, например, основанный на системе аксиом Пиано. В школьном курсе математики изучение арифметики натуральных чисел опирается, прежде всего, на наглядность. Однако основой изложения этого материала в учебниках и на уроках является ясное и последовательное логическое строение его. Причем обучение арифметике натуральных чисел исходит из самостоятельного происхождения этих чисел из счета предметов. Формирование понятия натурального числа начинается в начальной школе. В 5 классе проводится систематизация и расширение сведений о натуральном числе, полученных в начальной школе. Изучение натуральных чисел здесь связано с формированием таких важных для математики понятий, как «координатный луч», «уравнение» и «неравенство». При этом учащиеся должны твердо усвоить, что любое натуральное число может быть изображено точкой на координатном луче, причем каждому натуральному числу соответствует единственная точка на координатном луче, но не каждой точке координатного луча соответствует натуральное число. На этот момент важно обратить особое внимание, так как это готовит к пониманию необходимости введения новых чисел, то есть к расширению понятия числа. С учащимися выясняется также такое свойство множества натуральных чисел, как бесконечность. С помощью координатного луча сравниваются натуральные числа между собой, устанавливаются понятия «равно», «больше» и «меньше» для натуральных чисел. Важно, чтобы ученики усвоили такие понятия, как «числа, следующие за данным», «числа, предшествующие данному», умели ответить на вопросы: сколько чисел может непосредственно следовать за данным числом, сколько чисел может непосредственно предшествовать данному числу, кроме 1. На этом этапе дастся запись четного и нечетного чисел формулами: 2п и 2п + 1. Особое внимание следует уделить действиям над многозначными числами, трудным случаям умножения и деления, действиям с нулем и единицей и, в частности, «закону поглощения 0 (я + 0 = я, 0 + а = а)». Необходимо показать учащимся, что, например, действия 1 • а = а, 0 • а = 0 являются, по существу, следствиями из определения действия умножения, а а : 1 = а, а : а = 1,0 : а = О, а : К- из определения действия деления. После изучения действий над натуральными числами можно рассмотреть вопрос о замкнутости множества натуральных чисел относительно сложения и умножения и отметить, что в отношении вычитания — это свойство не выполняется. Большое внимание в этой теме следует уделить законам арифметических действий (переместительному, сочетательному, распределительному). В учебниках математики они формулируются как свойства сложения и умножения. Важно показать глубокое теоретическое значение законов, так как у учащихся обычно создастся впечатление, что законы нужны лишь для упрощения арифметических действий. В 5 классе законы арифметических действий записываются в общем виде с использованием буквенной символики. Рассмотрение коммутативного (переместительного) и ассоциативного (сочетательного) законов умножения целесообразно связать с геометрическим материалом, а именно, с вычислением площадей прямоугольников и объемов прямоугольных параллелепипедов. Целые числа и их свойства, делимость чисел, методика их изучения. 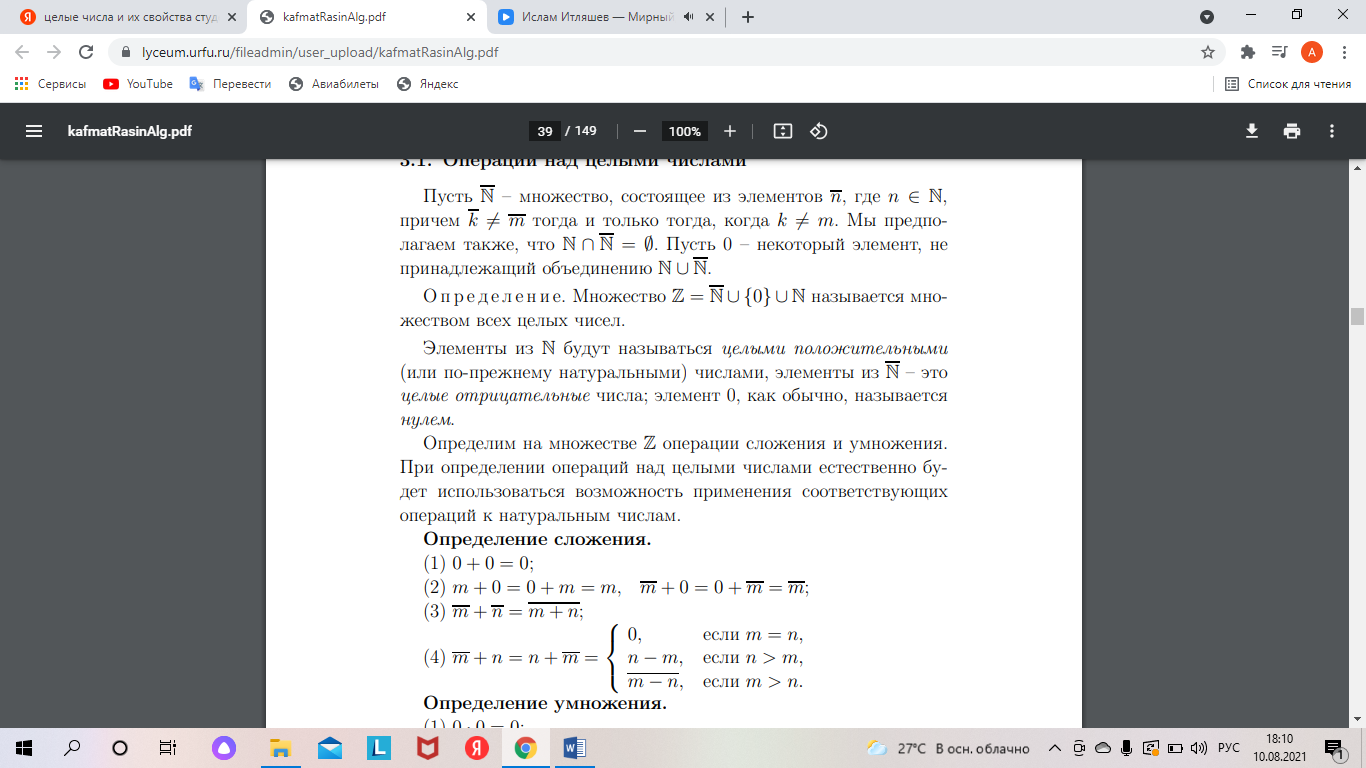  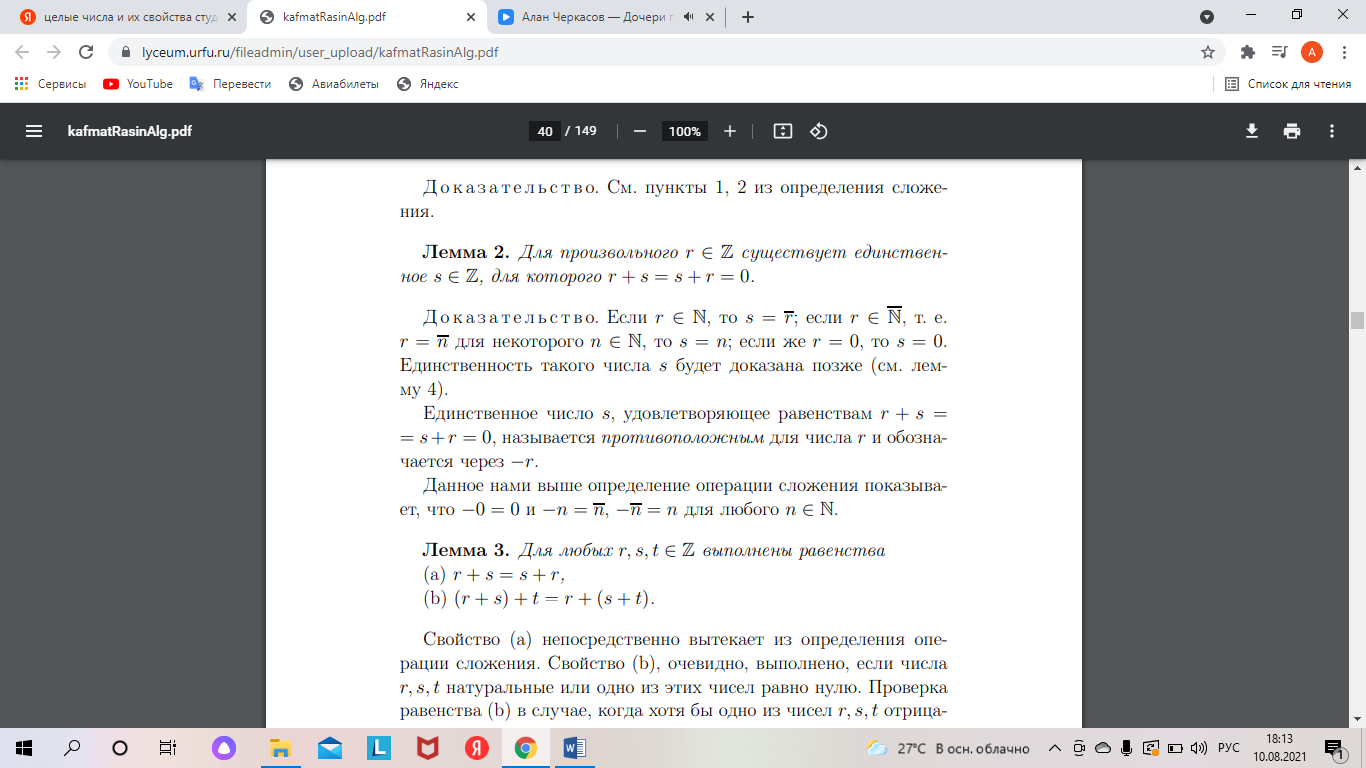      Делимость целых чисел.  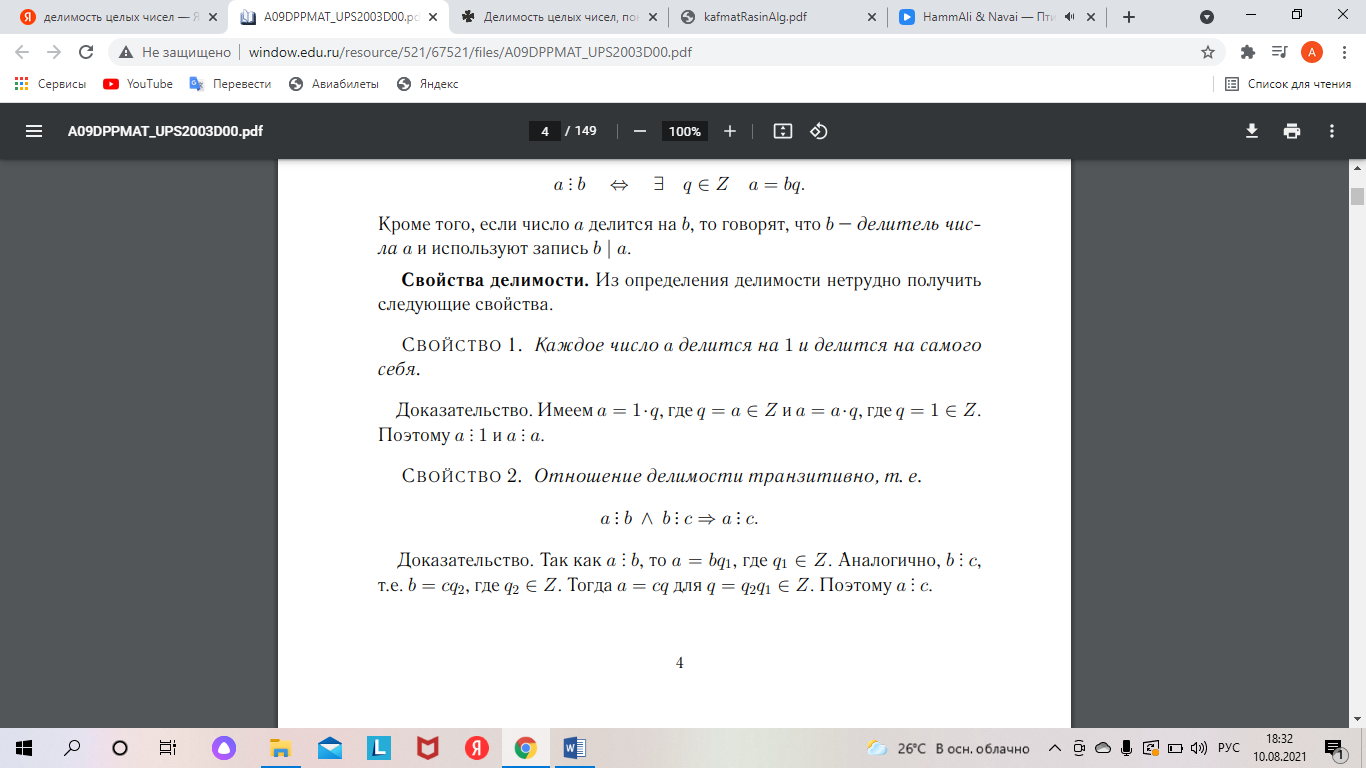     |
