Навчальний посібник 3є видання, перероблене І доповнене тернопіль навчальна книга богдан ббк 74. 262. 2ІЯ73 Б73
 Скачать 4.93 Mb. Скачать 4.93 Mb.
|
Підготовча робота до введення складених задач. На уроках ознайомлення зі складеними задачами важливо, щоб учні зрозуміли їхню основну відмінність від простих: ці задачі не можна розв'язати відразу, однією дією. Щоб відповісти на запитання задачі, спочатку знаходять число, якого немає в умові задачі. Розумінню цього сприяє підготовча робота, яка починається задовго до введення складених задач: 1. Розв'язування задач з недостатніми даними. Задача. На клумбі росло 12 квіток. Декілька квіток зрізали для букета. Скільки квіток залишилося на клумбі? Виконуючи такі вправи, учні дізнаються, що не завжди можна відразу дати відповідь на запитання задачі, бо може не вистачити числових даних. В наведеній задачі їх треба підібрати, а при розв'язуванні складених задач недостатні числа треба знайти, виконавши відповідну дію над даними у задачі числами. " 2. Вироблення вмінь розв'язувати прості задачі, які входять до складеної. 3. Постановка запитань до даної умови. Завдання. Постав запитання до умови задачі і розв'яжи задачу. Задача. На одній полиці було 4 книжки, а на іншій — на 2 книжки більше. Якщо учень поставить запитання: "Скільки всього книжок на двох полицях?", то вчитель з'ясовує, що треба знати для того, щоб відповісти на це запитання і чи відомо це з умови задачі. Вчитель підсумовує, що для відповіді на таке запитання необхідно виконати дві дії, тому для того, щоб отримати відповідь відразу, це запитання ставити не можна. 4. Розв'язування задач з двома запитаннями. Задача. Катруся засушила 7 дубових листків, а кленових — на 2 менше. а) Скільки кленових листків засушила Катруся ? б) Скільки всього листків засушила дівчинка ? Ознайомлення зі складеною задачею. Для ознайомлення учнів зі складеною задачею доцільно взяти таку, яка розв'язується різними діями першого Методика викладання математики в початкових класах 249 ступеня. Варто розпочати із задачі, що складається з простих задач на знаходження суми й остачі. Задача. Сашко приніс 6 морквин, а Оленка — 4 морквини. 8 морквин вони віддали кролям. Скільки морквин залишилося? Розгляньмо два способи введення складеної задачі. І спосіб. Учитель читає задачу, а хлопчик і дівчинка виконують відповідно ті дії, про які йдеться в умові. Повторюючи задачу, вчитель записує її коротко на дошці: Принесли — 6 м. і 4 м. Віддали — 8 м. Залишилося — ? Потім за цим записом задачу аналізують. Сашко приніс 6 морквин, а Оленка — 4 морквини. Про що можна дізнатися за цими даними? (Скільки всього морквин принесли Сашко й Оленка). Якою дією? (Дією додавання). Якщо буде відомо, скільки всього морквин принесли діти і скільки морквин вони віддали кролям, то про що можна дізнатися? Якою дією? (Учитель записує на дошці розв'язання, залучаючи дітей до його обгрунтування). Це є звичайний розбір складеної задачі. Однак про складену задачу діти ще не чули. Вчитель їх просто підводить до того, що в цій задачі мають бути дві дії. II спосіб. На столі стоїть кошик і лежать 6 та 4 морквини. — Складемо і розв'яжемо задачу про морквини. Сашко приніс 6 морквин і поклав їх у кошик. (Учитель показує 6 морквин і кладе їх у кошик). Оленка принесла 4 морквини і поклала їх у кошик. (Учитель інсценує). 8 морквин діти віддали кролям. (Учитель виймає з кошика 8 морквин). Отже, що нам відомо? Скільки морквин приніс Сашко? (6). Скільки морквин принесла Оленка? (4). Скільки морквин діти віддали кролям? (8). А що нам невідомо? (Вчитель заглядає в кошик). Скільки морквин залишилося в кошику? Це є запитання задачі. Ми склали задачу. Запишемо її коротко і повторимо зміст задачі. Потім учитель дає час подумати над її розв'язуванням і пропонує сказати, яку отримано відповідь. Як правило, учні швидко розв'язують задачу. Після цього бесіда продовжується. — Правильно, у кошику залишилось 2 морквини. Як ви дізналися про це? (Від числа 10 відняли 8). Звідки взялося число 10? В умові ж його не було. (До числа 6 додали 4). Отже, ми спочатку до числа 6 додали 4. Про що дізналися цією дією? (Скільки всього морквин поклали в кошик). Що робили потім? (Від числа 10 відняли 8. Отримали 2, тобто знайшли, скільки морквин залишилось у кошику). Щоб розв'язати цю задачу, ми виконали не одну, а дві дії. Причому ми не тільки дібрали дії, а й визначили порядок їх виконання, тобто склали план розв'язування. Запишемо розв'язання: 1)6 + 4= 10(м.); 2) 10-8 = 2 (м.). 250 РозділXI. Навчання учнів розв 'язувати текстові задачі Учитель спочатку з'ясовує, про що дізналися в першій дії, а тоді — в другій дії. Тут ознайомлення зі складеною задачею відбувається так само, як і ознайомлення з простою задачею. Потребу у виконанні двох дій і складанні плану розв'язування учні "відкривають" самі. У цьому й полягає перевага другого способу. Розвиток уявлень учнів про структуру задачі. У процесі розв'язування простих задач та ознайомлення зі складеною задачею діти отримують деякі уявлення про структуру задачі. Подальший розвиток цього уявлення відбувається під час розв'язування різних видів складених задач. Учителі пропонують деякі спеціальні запитання і завдання, проте вони здебільшого зводяться до вимоги розчленувати задачу на умову й запитання: повторення умови задачі, її запитання; читання задачі і виділення в ній запитання; читання умови задачі про себе, а вголос — тільки запитання; визначення, що в задачі відомо, а що невідомо. Щоб звернути увагу на основну відмінність складеної задачі від простої, ставлять, наприклад, такі запитання: Чи можна розв'язати задачу однією дією? Чому не можна розв'язати задачу однією дією? Яку маємо задачу — просту чи складену? Такі запитання корисні, але вони не охоплюють усіх компонентів поняття "задача". Роботу в цьому напрямку потрібно урізноманітнити. Розгляньмо питання про кількість числових даних. Учні швидко усвідомлюють, що в арифметичній задачі має бути не менше, ніж два числа. Проте іноді вони забувають про це і намагаються розв'язати задачу тільки з одним числовим даним. З цією метою доцільно також розглядати задачі з недостатньою кількістю даних. Задача 1. У дівчинки було 20 коп. Вона купила олівець. Скільки грошей залишилося у дівчинки? Задача 2. На першому полі збирали пшеницю 7 комбайнів, на другому — комбайнів було більше, ніж на першому. Скільки всього комбайнів збирали пшеницю ? Учитель ознайомлює дітей із задачею, а потім запитує: "Чи можна розв'язати цю задачу? Чому її не можна розв'язати? Що треба ще знати, щоб знайти відповідь? Як треба доповнити задачу?". Задача може містити і два числа, але вони не перебувають у тому відношенні, яке передбачає запитання. Задача. На прогулянку в ліс пішло 2 хлопчики. Один з них знайшов 5 грибів, а інший — менше. Скільки грибів знайшли хлопчики разом? У роботі над деякими задачами можна вказати прийоми, за допомогою яких з'ясовують, що числові дані задачі перебувають у певних зв'язках, а їх вибір визначається запитаннями. Для задач, пов'язаних різницевим або кратним відношенням, ці прийоми зводяться до постановки запитання: що в задачі сказано про залежність між числами? Учні відповідають: "У задачі сказано, що друге число на 3 менше, ніж перше". До задач з пропорційними величинами ставлять узагальнені запитання: "Як за ціною і кількістю знайти вартість?"; "Про що можна дізнатись, якщо відомі шлях і швидкість?" та ін. Методика викладання математики в початкових класах 251 Певне значення для розвитку уявлень дітей про структуру задачі має "будова запитання". При цьому виділяють дві групи задач. Перша група — умова і запитання роздільні, тобто запитання виділено в окреме речення і не містить числових даних. Друга група — це задачі, в яких умова і запитання розділені не повністю, у запитанні є числові дані. Варто виконати кілька завдань на перебудову задачі, щоб запитання не містило числових даних. Задача. У магазині було 2 рулони тканини: 40 м і 60 м. Скільки метрів тканини залишилось, якщо за день було продано 90 м ? Про що йдеться в задачі? (Про тканину). Скільки рулонів і по скільки метрів тканини у кожному? (Два рулони: 40 м і 60 м). Що відомо ще про тканину? (За день продали 90 м тканини). Що треба знайти? (Скільки метрів тканини залишилося). Після розв'язання задачі вчитель пропонує учням прочитати запитання задачі і сказати, яка його частина належить до умови, а яка — до запитання. У підручниках для початкових класів переважна більшість задач містить запитання зі словом "скільки", решта задач містить запитання з такими словами та виразами: "Чому дорівнює...?", "Знайти...", "Обчислити...". Кількість цих задач з кожним наступним роком зростає, але за змістом вони належать до практичних задач. Це є однією з причин того, що вимогу задачі учні розуміють як речення, яке починається зі слова "скільки". Щоб запобігти такому стереотипу, слід іноді перебудовувати запитання. Наприклад, замість "Скільки літрів бензину залишилося?" запитуємо: "Знайти остачу бензину", "Чому дорівнює остача бензину?". Узагальнювала ним словом тут є "остача". Запитання "Скільки грошей учень заплатив за всю покупку?" можна перебудувати так: "Обчисліть вартість усієї покупки учня". Запитання без слова "скільки" пропонує вчитель, а перебудоване запитання, що містить слово "скільки", формулюють учні. Для розвитку уявлень дітей про структуру задачі дуже корисно використовувати вправи на перетворення та складання задач. Для простих задач основними вправами є добір запитання до умови або добір умови до запитання. З переходом до задачі на дві дії учням пропонують такі завдання: змінити в задачі умову або запитання так, щоб вона розв'язувалась двома діями, або, навпаки, перетворити складену задачу на просту. У 3 класі запроваджується складання обернених задач. При складанні обернених задач на 2 — 3 дії варто користуватися коротким записом задачі. Після того, як задачу розв'язано, вчитель закреслює одне з даних, на його місці ставить знак запитання, а на місці знака запитання записує знайдене шукане. За цим зміненим записом діти складають обернену задачу. До інших творчих завдань належать: складання задач заданим розв'язком або за малюнком; порівняння задач; перетворення даної задачі на споріднену (в них величини пов'язані однаковою залежністю). Розв'язування даної задачі та складання задачі, оберненої до неї, пов'язано з необхідністю ще раз розглянути залежності між величинами, але під іншим кутом зору. Це сприяє глибшому усвідомленню не тільки залежності між величинами і способу розв'язування задачі, а й її структури. 252 РозділXI. Навчання учнів розв 'язувати текстові задачі Прийоми розвитку уявлень учнів про процес розв'язування задач. Розвиток уявлень учнів про "технологію" розв'язування задач і формування вмінь розв'язувати задачі становлять фактично єдиний процес. Проте серед прийомів, спрямованих на забезпечення цього процесу, можна виділити такі, які більше стосуються його першої частини. Це розв'язування складених задач за даним планом, графічне зображення повного аналізу і плану розв'язування. Розв'язування задач за даним планом слід розглядати і як спеціальне завдання, і як методичний прийом, завдяки чому забезпечується усвідомлення учнів у необхідності складати план, а також розкривається "технологія" розв'язування складеної задачі, її структура. У 2-4 класах бажано розв'язати за даним планом хоча б одну задачу на тиждень. Повний аналіз і його графічне зображення. Задача. Купили 40 кг помідорів. Восьму частину маси усіх помідорів залишили для їжі, а решту — зас'олили порівну в 7 банок. Скільки кілограмів помідорів поклали в кожну банку? Що треба знати, щоб відповісти на запитання задачі? (Треба знати, скільки банок було і скільки кілограмів помідорів засолили). Скільки банок було — відомо, а скільки кілограмів помідорів засолили — невідомо. Що треба знати, щоб знайти, скільки всього засолили помідорів? (Треба знати, скільки кілограмів помідорів купили і скільки залишили для їжі). Скільки кілограмів помідорів купили — відомо, а скільки залишили для їжі — невідомо. Що треба знати, щоб знайти, скільки кілограмів помідорів залишили для їжі? (Треба знати, скільки всього кілограмів помідорів купили і яку частину їх залишили для їжі. Обидві величини відомі). Повний аналіз задачі графічно зображено на мал. 125. 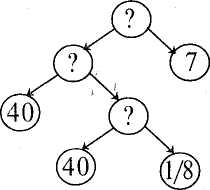 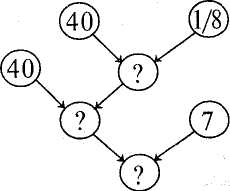 Мол. 125 Мал. 126 Кружечки зі знаком запитання позначають головне і проміжні запитання задачі. Від кожного з них проведено дві стрілки. В кінці стрілок у кружечках записують числа (відомі або невідомі), необхідні для знаходження відповіді на запитання. Зауважимо, що при відшуканні способу розв'язування від числових даних до запитання графічне зображення буде мати такий вигляд, як показано на малюнку (мал. 126). Відповідно до проведеного аналізу план розв'язування задачі буде такий: Методика викладання математики в початкових класах 253 План розв'язування 1) Скільки кілограмів помідорів залишилося для їжі? 2) Скільки кілограмів помідорів засолили в банках? 3) Скільки кілограмів помідорів поклали в кожну банку? Способом повного аналізу задачі з його графічним зображенням доцільно розв'язати три-чотири задачі в 3-4 класах. Вся робота виконується під керівництвом учителя. Для самостійної роботи молодшим школярам такі завдання не пропонують. Розгляньмо початкове ознайомлення учнів зі способом повного аналізу задачі з його графічним зображенням (мал. 127). Задача. Посадили 6 саджанців яблунь і 2 ряди саджанців груш по 12 саджанців кожен. Скільки саджанців дерев посадили ? Бесіда. Проведемо відшукання способу розв'язування задачі. Що запитується в задачі? (Скільки дерев посадили?). Позначимо запитання відповідним знаком і візьмемо його в кружечок (мал. 127). Що треба знати, щоб знайти кількість саджанців дерев? (Треба знати, скільки посадили саджанців яблунь і груш окремо). 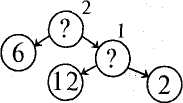 Мал. 127 Учитель проводить від цього кружечка дві стрілки і до кожної стрілки креслить по кружечку, а потім запитує: — Чи знаємо скільки саджанців яблунь посадили? (6). Запишемо це у лівому кружечку. Чи відомо, скільки саджанців груш посадили? (Ні). Поставимо в правому кружечку знак запитання. Що треба знати, щоб знайти, скільки саджанців груш посадили? (Скільки рядів груш посадили і по скільки саджанців груш садили в ряду). Учитель від правого кружечка проводить дві стрілки і креслить два кружечки. — Чи знаємо, скільки рядів саджанців груш? (2). Скільки саджанців груш садили в ряд? (12). Запишемо в кружечки числа 12 і 2. Тепер можна скласти план розв'язування задачі. Спочатку дізнаємося, скільки саджанців груш посадили в 2 ряди. Це перше запитання (учитель ставить цифру 1 біля відповідного кружечка). Потім дізнаємося, скільки всього дерев посадили. Це друге й останнє запитання задачі. Отже, щоб розв'язати складену задачу, потрібно її розкласти на прості задачі і до кожної знайти відповідь. §41. Розв'язування типових задач У підручниках для початкових класів є такі задачі, які традиційно називають типовими. До типових належать задачі на знаходження четвертого пропорційного (на спосіб прямого й оберненого зведення до одиниці та спосіб відношень), на пропорційне ділення, на знаходження числа за двома254 РозділХІ. Навчання учнів розв 'язувати текстові задачі різницями, на знаходження середнього арифметичного. Методика розв'язування типових задач принципово не відрізняється від розгляду будь-яких інших задач нового виду, тобто передбачає підготовку, ознайомлення і розвиток умінь. Проте деякі особливості роботи над типовими задачами необхідно враховувати. Розв'язування типових задач, пов'язаних з пропорційними величинами, грунтується на знанні відповідних зв'язків між величинами. Ознайомлення з величинами проводиться одночасно з розкриттям зв'язків між ними. Зв'язки формулюють у вигляді висновків. Наприклад, якщо відомо ціну і кількість, то вартість можна знайти дією множення. Типові задачі мають деякі характерні ознаки, що враховуються на підготовчому етапі роботи. Слід також мати на увазі взаємозв'язки між окремими типовими задачами. Розв'язування задач на знаходження четвертого пропорційного способом зведення до одиниці запроваджується в 3 класі. Розгляду задач передує тривала робота над їх розв'язуванням на визначення ціни, кількості та вартості. Вона проводиться у вигляді гри "в магазин". Під час гри учні вчаться розв'язувати задачі на знаходження вартості, ціни і кількості. Характерною особливістю в цій роботі є те, що, аналізуючи задачі, вчитель вимагає від учнів пояснення, які величини відомі і які треба знайти. Для першого розгляду задачі на спосіб прямого зведення до одиниці доцільно відвести окремий урок. Заслуговує на увагу досвід ознайомлення із задачею на основі складання її з відповідних двох простих задач. Задача. Дівчинка купила 5 конвертів без марки і заплатила ЗО коп. Скільки копійок коштує один конверт ? Повторіть задачу. Назвіть відомі і невідомі величини. (В задачі відомо, що дівчинка купила 5 конвертів. Вартість конвертів ЗО коп. Невідомо, яка ціна одного конверта). Розв'яжіть задачу і поясніть розв'язання. ЗО : 5 = 6 (коп.). Відповідь. Ціна конверта 6 коп. Пояснення. Щоб знайти ціну конверта, слід вартість конвертів поділити на їхню кількість. Розв'яжемо другу! задачу, пов'язану з першою. Задача. Ціна одного конверта без марки 6 коп. Дівчинка купила 9 конвертів. Знайти вартість покупки. 6 • 9 = 54 (коп.). Відповідь. За 9 конвертів дівчинка заплатила 54 коп. З розв'язаних двох простих задач можна скласти одну задачу на дві дії. Задача. Дівчинка за 5 конвертів без марки заплатила ЗО коп. Потім вона купила ще 9 конвертів. Скільки копійок коштують 9 конвертів? Задачу можна записати коротко: 5 к. — ЗО коп. 9к.-? Що можна знайти першою дією? (Ціну одного конверта)іЛі можна тоді знайти відповідь на запитання задачі? (Можна, якщо відомі-ціна одного конверта та їхня кількість). Методика викладання математики в початкових'класах 255 Далі вчитель пропонує скласти план розв'язування задачі і записати розв'язання. Зауважимо, що, аналізуючи задачу, можна- використати предметну ілюстрацію, виставляючи вказану кількість конвертів на набірному полотні. Для первинного закріплення вчитель пропонує розв'язати самостійно задачу, спираючись на короткий запис і план розв'язування. Задача. 5 м тканини коштують 60 грн. Скільки гривень коштують 7м такої тканини? 5 м — 60 грн. 7м — ? План розв'язування 1) Скільки коштує 1 м тканини? 2) Скільки коштують 7 м тканини? Подальше закріплення вмінь розв'язувати задачі проводять на матеріалі інших величин, що перебувають у пропорційній залежності (маса предмета, кількість предметів, їх загальна маса; витрата тканини на одну річ, кількість речей, загальна витрата матерії; продуктивність праці, час роботи, маса виробленої продукції; швидкість, час, відстань; довжина, ширина і площа прямокутника). У процесі закріплення діти вчаться записувати коротко задачу, виявляти характер залежностей між величинами, формулювати ці залежності словами, пояснювати хід розв'язування. Під час розв'язування задач на знаходження четвертого пропорційного їх короткий запис подають іноді табличним способом з вказівкою величини, значення якої є однаковими (сталими). Задача. Першого разу купили 3 пакети цукру масою 6 кг. Другого разу купили 10 кг цукру в таких самих пакетах. Скільки пакетів цукру купили другого разу? (Обернений спосіб зведення до одиниці). | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Маса пакета | Кількість | пакетів | Маса | цукру | в пакетах |
| Однакова | 3 | | | 6кг | |
| 9 | | | 10кг | |
У таких і подібних задачах сталими величинами можуть бути кількість пакетів і маса цукру у всіх пакетах. Для кожної сталої величини можна скласти два види задач на знаходження четвертого пропорційного. Таким чином, матимемо 6 видів задач на знаходження четвертого пропорційного.
Якщо в задачах з пропорційними величинами одну з величин задати не однаковими числовими значеннями, а їх різницевим відношенням, то отримаємо ускладнену задачу. 256
Розділ XI. Навчання учнів розв 'язувати текстові задачі
Задача. Токар за 2 год зробив 18 деталей. Скільки деталей він зробить за 6 год, якщо щогодини робитиме на 1 деталь більше, ніж раніше ?
Ознайомлення з ускладненими задачами запроваджується в 3 класі, причому розглядають їх здебільшого фронтально.
У 4 класі розглядають задачі на знаходження четвертого пропорційного, які розв язують способом відношення.
Задача. За поживністю З кг ячменю замінюють 4 кг вівса. Скільки кілограмів ячменю потрібно, щоб замінити 12 кг вівса ?
На дошці запис:
4 кг — 3 кг. 12 кг-?
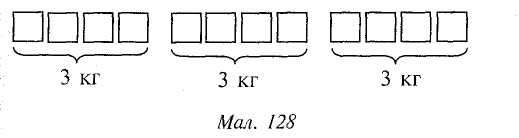
Учні не в змозі розв'язати цю задачу способом зведення до одиниці. Для кращого осмислення змісту задачі її можна зобразити графічно (мал. 128).
Кожних 4 кг вівса можна замінити 3 кг ячменю. З'ясовуємо, скільки разів по 4 кг вівса вміститься в 12 кг. (З рази). Якщо кожних 4 кг вівса замінюють З кг ячменю, а по 4 кг треба взяти 3 рази, то стає очевидним план розв'язування:
1) Скільки разів по 4 кг вівса вміщується в 12 кг?
2) Скільки кілограмів ячменю потрібно, щоб замінити 12 кг вівса?
У 4 класі учні ознайомлюються також з розв'язуванням ускладнених задач на знаходження четвертого пропорційного на зразок задачі, поданої нижче.
Задача. З косарки за 7 год скосили 42 га трави. Скільки гектарів трави скосить одна така косарка за 4 год?
З к., 7 год — 42 га. 1 к., 4 год — ?
Розв'язують ці задачі способом послідовного зведення до одиниці.
Ознайомлення дітей із задачами на пропорційне ділення проводять у 4 класі. Спочатку вони виконують підготовчі завдання.
Завдання. Розглянути малюнок, виконати необхідні обчислення і сказати, скільки олівців в одній коробці (мал. 129).
У процесі аналізу завдання вчитель ставить такі запитання: Скільки коробок зліва? Справа? Скільки всього коробок? Як дізнатися, скільки олівців в одній коробці?
Методика викладання математики в початкових класах
257
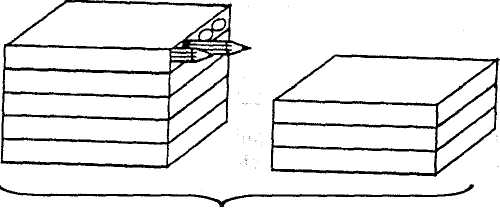
48 Мал. 129
Задача. Купили два відрізи однакової матерії. У першому відрізі було З у другому —6м матерії. За обидва відрізи заплатили 72 грн. Скільки гривень коштує 1 м матерії?
Учитель ставить запитання: Скільки відрізів матерії купили? Скільки всього метрів матерії купили? Як знайти ціну 1 м матерії?
Задача. Дівчинка купила 3 зошити для себе і 2 зошити для однокласниці. За всі зошити вона заплатила 1 грн. Скільки грошей має віддати дівчинці однокласниця за зошити?
Задачу пропонують розв'язати самостійно, але перед цим слід з'ясувати, як знайти ціну одного зошита, що треба знати, щоб обчислити вартість покупки.
Розв'язування підготовчих задач активізує діяльність учнів при опрацюванні задач нового типу.
Розгляньте два варіанти фрагментів уроку на тему "Ознайомлення із задачею на пропорційний поділ".
1 варіант
Учням пропонують розв'язати задачу: "Купили 3 зошити в лінійку і 2 зошити в клітинку за тією самою ціною. За зошити в лінійку заплатили 54 коп. Скільки грошей заплатили за зошити в клітинку?" (за таблицею).
| Ціна | Кількість | Вартість |
| Однакова | 3 2 | 54 коп. 1 |
Діти розв'язують задачу окремими діями з поясненням у запитальній формі.
У заздалегідь заготовлену таблицю на дошці вчитель записує суму вартостей всіх зошитів, знайдену учнями, і знаки запитання.
258
Розділ XI. Навчання учнів розв 'язувати текстові задачі
| Ціна | Кількість | Вартість |
| Однакова | 3 2 | ? 1 9 і 90 коп. |
Учні складають задачу на пропорційний поділ з двома запитаннями: "Скільки грошей заплатили за зошити в лінійку? Скільки грошей заплатили за зошити в клітинку?".
Вчитель повідомляє, що ці два запитання можна замінити одним: "Скільки грошей заплатили за зошити в лінійку і клітинку окремо?". Після цього формулюється задача: "Купили З зошити в лінійку і 2 зошити в клітинку за тією самою ціною. За всі зошити заплатили 90 коп. Скільки грошей заплатили за зошити в лінійку і в клітинку окремо?".
— Чи можна одразу дізнатися, скільки грошей заплатили за зошити в лінійку? (Ні).
— Що треба знати, щоб дізнатися, скільки грошей заплатили за зошити в лінійку? (Ціну зошита і кількість куплених зошитів у лінійку).
— Чи відома кількість зошитів у лінійку? (Відома). ;
— Чи відома ціна зошита в лінійку? (Невідома).
— Що сказано про ціну зошита в задачі? (Ціна зошита в лінійку і клітинку однакова).
-^ Чи можна дізнатися, скільки зошитів купили на 90 коп.? (Можна). Складіть план розв'язування задачі.
II варіант
Учням пропонують одразу розв'язати готову задачу на пропорційний поділ.
Підготовчими вправами до ознайомлення дітей із задачами на знаходження невідомого за двома різницями будуть такі:
/. Перший магазин продав З мішки цукру, а другий — 5 таких самих мішків. Який із магазинів продав більше кілограмів цукру? Чому?
2. Перший магазин продав на 2мішки цукру більше, ніж другий. З'ясувалося, що він продав на 100 кг більше. Скільки кілограмів цукру в одному мішку?
Треба проілюструвати цю задачу предметно або за допомогою відрізків (мал. 130).
І--------------------------------1----------1----------1
Мал. 130
Безпосереднє ознайомлення із задачами на знаходження невідомого за двома різницями проводиться на основі розв'язування трьох задач, поданих нижче.
Задача 1. Перший покупець купив 2 м тканини і заплатив 18 грн. Скільки гривень коштує 1 м тканини ?
Методика викладання математики в початкових класах
259
Задача 2. Перший покупець купив 5 м тканини, а другий — 3 м такої самої тканини. Перший покупець заплатив на 18 грн. більше, ніж другий. Скільки гривень коштує 1 м тканини ?
Задача 3. Перший покупець купив 5 м тканини, а другий 3 м такої самої тканини. Перший покупець заплатив на 18 грн. більше, ніж: другий. Скільки гривень заплатив другий покупець ?
Ознайомлюючи учнів із задачею на знаходження величини за двома різницями, вчитель прочитав задачу такого змісту: "З першої ділянки зібрали 6 кошиків моркви, а з другої — 4 таких самих кошики. З першої ділянки зібрали на 40 кг моркви більше, ніж з другої. Скільки кілограмів моркви зібрали з кожної ділянки окремо?" — і запропонував учням розглянути малюнок (мал. 131).
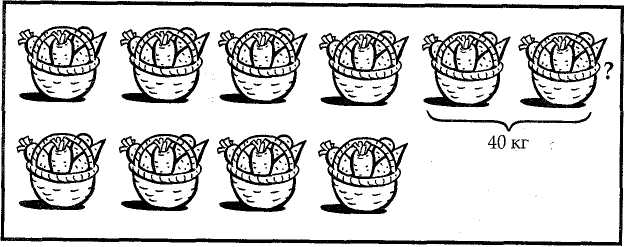
Мал. 131
— Чому з першої ділянки зібрали на 40 кг моркви більше, ніж з другої?
— Маса скількох кошиків моркви, зібраної з першої ділянки, така сама, як і маса моркви, зібраної з другої ділянки? "
— Маса скількох кошиків моркви дорівнює 40 кг?
— Складіть план розв'язування задачі.
Задачі на знаходження середнього арифметичного. Розв'язування цих задач ґрунтується на правилі, поданому нижче.
Щоб знайти середнє арифметичне кількох чисел, треба їх суму поділити на кількість цих чисел.
Це правило вводиться на основі аналізу готового розв'язання задачі.
Задача. Велосипедист одну годину їхав зі швидкістю 15 км/год, дві години зі швидкістю 13 км/год і ще одну годину зі швидкістю 11 км/год. Знайти середню швидкість велосипедиста.
Розв'язання
1) Скільки всього годин їхав велосипедист?
1+2+1=4 (год).
2) Скільки всього кілометрів проїхав велосипедист?
15+13-2+11 =52(км).
3) Скільки кілометрів за годину в середньому проїжджав велосипедист?
52 : 4 = 13 (км/год).
160
РозділXI. Навчання учнів розв'язу.ватиітекетові.задачі
и Розв'яжемо задачу, склавши числовий вираз: п
(15 + 13 • 2 + 11) : (1 + 2 + 1) = 13 (км/год);
Для закріплення пропонується задача. к; Задача. Маса першого кроля дорівнює 2 кг 200 г, а < •Знайти середню масу цих кролів.
Розв'язання (2 кг 200 г + 1 кг 600 г) : (1 + 1) = 1 кг 900 г.
Задачі цього виду застосовуються для знаходження середньої урожайності, середньої швидкості, середньої маси.
Опрацьовуючи типові задачі не слід вдаватися до їх класифікації, тобто не вживати термінів "задача на пропорційне ділення", "задача на знаходження невідомого за двома різницями" тощо.
У початкових класах виділяють ще задачі з певним конкретним сюжетом. Це задачі на зустрічний рух, на час, задачі з геометричним змістом.
Розгляньмо задачі на рух. Розв'язуванню задач на зустрічний рух передує тривала робота з розв'язування простих та складених задач на знаходження швидкості, часу та відстані. Поняття швидкості вводять на основі життєвого досвіду дітей та безпосередніх практичних дій.
Для формування навичок доцільно усно розв'язувати задачі за таблицями. Наведемо зразки таблиць.
1. Знайдіть швидкість.
| | Назва | Швидкість | Час | Відстань |
| | Велосипедист | 9 | 2год | 28 км |
| | Автомобіль | 9 | 3 год | 210 км |
| ■' 2. Знайдіть відстань. | ||||
| | Назва | Швидкість | Час | Відстань |
| | Пішохід ' | 5 км/год | 4 год | 9 |
| і'А | Електропоїзд | 120 км/год | 3 год | ? |
| 3. Знайдіть час. | ||||
| | Назва | Швидкість | Час | Відстань |
| | Лижник | 13 км/год | ? | 26 км |
| | Поїзд | 60 км/год | ? | 240 км |
Методика викладання математики в початкових класах
261
4. Знайдіть невідомі величини.
| Назва | Швидкість | Час " | Відстань |
| Велосипедист | 10 км/год | 3 год | ? |
| Автомобіль | 36 км/год | ? | 72 км |
| Теплохід "Комета" | ? | 4 год | 280 км |
У ході підготовчої роботи ілюструють зміст таких виразів, як "виїхали одночасно", "рухаються назустріч один одному", "рухаються в протилежних напрямах" тощо. Практичні дії супроводяться зображенням відрізків (довжина шляху) і стрілками (напрям руху). З відповідними ілюстраціями потрібно розглянути кілька задач такого виду:
/. З двох міст об 11 год виїхали назустріч один одному два поїзди. Вони зустрілися о 15 год. Скільки годин перебував у дорозі до зустрічі кожний поїзд?
2. Два пішоходи рухаються назустріч один одному. Швидкість першого пішохода дорівнює 5 км/год, а другого — 4 км/год. На скільки кілометрів вони зближуються за 1 год? За 2 год? За З год?
3. Два катери рухаються по річці у протилежних напрямах. Швидкість першого катера дорівнює 24 км/год, а другого — 37км/год. На скільки кілометрів вони віддаляються один від одного за 1 год? За 2 год? За 3 год?
Кожна із задач на зустрічний рух і рух у протилежних напрямах (у разі віддалення рухомих тіл) має три види.
I вид — дано швидкість кожного з тіл і час руху, шукане — відстань.
II вид — дано час руху, відстань, яку подолали разом обидва тіла, і швидкість одного з тіл, шукане — швидкість іншого тіла.
III вид — дано швидкість кожного з тіл і відстань, шукане — час руху. Заслуговує на увагу досвід послідовного введення задач. Спочатку на двох-
трьох уроках опрацьовують перший вид задач. На основі цього виду на наступних уроках вводять послідовно другий і третій види задач. Розгляньмо такий підхід на конкретних задачах.
Задача. З двох міст одночасно назустріч один одному виїхали велосипедист і мотоцикліст, які зустрілися через 3 год. Швидкість велосипедиста дорівнює 12 км/год, а мотоцикліста — 50 км/год. Скільки кілометрів становить відстань між містами ?
Повторюючи задачу, вчитель спирається на ілюстрацію (мал. 132).
Аналіз проводять від числових даних.
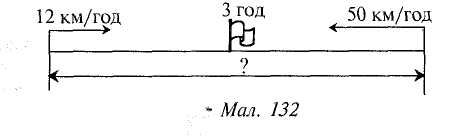
Що відомо про рух велосипедиста? (Швидкість і час руху). Про що звідси можна дізнатися? (Про відстань, яку проїхав велосипедист до зустрічі). Що відомо про рух мотоцикліста і що можна знайти? (Відомі швидкість і час, можна знайти відстань). Чи можна знайти відстань між містами? Повідомити план розв'язування задач і записати розв'язання. ...'■.....„ _ ..(
Розв'язання чо'пі/. \
1) 12 • 3 = 36 (км) — проїхав велосипедист; —-......—---^
2) 50 • 3 = 150 (км) - проїхав мотоцикліст; шхоїиз [ і
3) 36 + 150 =186 (км) — відстань між містами.
Після повторення розв'язання вчитель повідомляє, що задачу можна розв'язати іншим способом.
Спробуємо знайти другий спосіб розв'язування задачі. Велосипедист і мотоцикліст рухалися 3 год. Чи можна знайти, на скільки кілометрів зближувалися велосипедист і мотоцикліст за одну годину? (Можна. Для цього треба додати відстані, які подолали за годину окремо велосипедист і мотоцикліст). Велосипедист і мотоцикліст зближувалися 3 год. Як знайти відстань, яку вони подолали за цей час?
Розв'язання
1) 12 + 50 = 62 (км) — зближувалися велосипедист і мотоцикліст за 1 год;
2) 62 • 3 = 186 (км) — відстань між містами.
Підсумовуючи розв'язання задачі другим способом, учитель звертає увагу на те, що велосипедист і мотоцикліст проїхали 3 рази по 62 км.
На уроці, присвяченому розгляду задач другого виду, спочатку учні розв'язують задачі першого виду.
Задача. Дві велосипедні команди виїхали одночасно з двох селищ назустріч одна одній і зустрілися через 2 год. Перша команда їхала зі швидкістю 12 км/год, а друга — 13 км/год. Знайти відстань між селищами.
Вивчення, аналіз і розв'язування задачі проводять з опорою на графічну ілюстрацію (мал. 133).
12 км/год
13 км/год
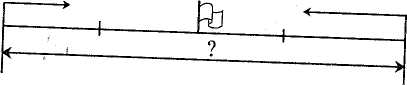
Розв'язавши задачу, учні дізналися, 50 км.
— Складемо обернену задачу на знаходження (мал. 134).
12 км/год
Мал. 133
що відстань між селищами дорівнює швидкості другої команди
Мал. 134
Методика викладання математики в початкових класах
263
Задача. Дві велосипедні команди виїхали одночасно з двох селищ назустріч одна одній і зустрілися через 2 год. Відстань між селищами дорівнює 50 км. Перша команда їхала зі швидкістю 12 км/год. Скільки кілометрів за годину проїжджала друга команда?
Колективно учні знаходять два способи розв'язування задачі. ,
Перший спосіб
1) 12 • 2 = 24 (км) — проїхала до зустрічі перша команда;
2) 50 - 24 = 26 (км) — проїхала до зустрічі друга команда;
3) 26 : 2 = 13 (км/год) — швидкість другої команди. Другий спосіб
1) 50 : 2 = 25 (км) — зближувалися команди за годину;
2) 25 — 12 = 13 (км/год) — швидкість другої команди. Аналогічно опрацьовують задачу на знаходження часу руху тіл.
У ході закріплення вмінь розв'язувати задачі на зустрічний рух та руі У протилежних напрямах варто практикувати різні творчі роботи.
