Навчальний посібник 3є видання, перероблене І доповнене тернопіль навчальна книга богдан ббк 74. 262. 2ІЯ73 Б73

• Название: Навчальний посібник 3є видання, перероблене І доповнене тернопіль навчальна книга богдан ббк 74. 262. 2ІЯ73 Б73
• Анкор: M_V_Bogdanovich_M_V_Kozak_Ya_A_Korol_metod.doc
• Дата: 03.02.2017
• Размер: 4.93 Mb.
• Имя файла: M_V_Bogdanovich_M_V_Kozak_Ya_A_Korol_metod.doc
• Тип: Навчальний посібник; #2000
• страница: 21 из 30

§38. Культура запису розв'язань задач

: Текстові задачі в початковому курсі математики розв'язують окремими діями ^без пояснення, з поясненням, за письмовим планом); способом складання виразу (без пояснення, з поясненням, готовий вираз); деякі прості задачі — способом складання рівнянь.

Розгляньмо вимоги до оформлення письмового розв'язання задач.

1-й клас. У першому класі початкової школи розв'язують тільки прості задачі. Запис розв'язання виконують у вигляді рівності, розміщеної посередині рядка.

Першокласникам іноді пропонують проілюструвати задачу малюнком. Для позначення предметів, про які йдеться в задачі, здебільшого викорис­товують кружечки, палички, трикутники, квадрати. У цьому разі розв'язання записують під малюнком (мал. 118).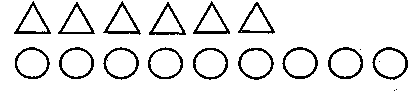



Мал. 118

2-й клас. Ще в процесі розв'язування простих задач учням варто показати, як коротко записувати задачу в один рядок, табличним способом і у вигляді структурного запису. Вони не роблять короткий запис задачі у зошиті, а розглядають його на дошці. З опорою на цей запис повторюють задачу, але розв'язання виконують так само, як і в першому класі.

Після ознайомлення зі складеною задачею діти вчаться записувати коротко задачі в зошиті, але виконують такі завдання за зразком і під керівництвом учителя. На цей час запроваджується найменування предметів у відповідях дій. Назви предметів записують однією буквою з крапкою в дужках після числа: 13 — 6 = 7 (в.). У відповідях до задачі назви предметів пишуть повністю (7 вагонів). Слова, що починаються на голосний, скорочують, як правило, до наступного голосного (яблуко — ябл., ялина — ял.). У короткому записі задач назви предметних дій (купили, продали, відрізали тощо) краще записувати повним словом. Якщо предмети, про які йдеться в задачі, відрізняються певною ознакою, то в короткому записі слід вказувати як ознаку, так і предмет. Для схематичного запису задач на знаходження суми запроваджується також фігурна дужка.

Для одного і того самого виду задач необов'язково застосовувати єдину форму короткого запису. Краще, щоб учні звикали до думки, що коротко задачу можна записувати по-різному. •■ • ■

Методика викладання математики в початкових класах

233

Задача. У бідоні міститься 9 л молока, а в каструлі — на 6л менше. Скільки літрів молока у бідоні і в каструлі разом ?

Б.-9 л.

К. — на 6 л менше.

Разом — ?

Б.-9 л.

К. — на 6 л менше.

Розв'язання задач записують окремими діями без пояснення (пояснення дають в усній формі).

1) 9 - 6 = 3 (л);

2) 9 + 3 = 12 (л). Відповідь. 12 л молока.

Застосування короткого позначення предметів може бути для дітей нелегкою справою. Тому вчитель здебільшого сам повідомляє дітям, як коротко позначити предмети у схематичному записі задачі чи в її розв'язанні.

У кінці вивчення нумерації в межах 100 ознайомлюють учнів із розв'я­занням задач складанням виразу.

У подальшій роботі вчитель сам визначає, як оформити запис розв'язання: окремими діями чи складанням виразу. Зрозуміло, що всі складені задачі з буквеними даними розв'язують складанням виразу.

Розв'язання однієї і тієї самої задачі й окремими діями, і складанням виразу практикують в окремих випадках як вид творчої роботи.

У другому півріччі запроваджують короткий запис відповіді задачі. Записують здобуте число і найменування.

У підручниках для 2-4 класів запроваджується така форма завдання, як розв'язування задач за даним планом. У 2 класі учні такий план взагалі не переписують у зошит, а учні 3 і 4 класів переписують його у зошит лише на вимогу вчителя.

3-й клас. У 3 класі учні вчаться записувати повну відповідь і короткі пояснення розв'язання. Із записом повної відповіді ознайомлюють дітей на початку навчального року. Записувати повну відповідь до кожної задачі не варто. На уроках треба практикувати як короткі, так і повні відповіді, а в домашніх і контрольних роботах повну відповідь записувати обов'язково.

Навчати коротко записувати пояснення ходу розв'язування задачі можна почати в середині першого семестру.

Задача. На 45 грн. купили набори олівців ціною по 5 грн. Стільки ж купили наборів фарб ціною по 8 грн. Скільки гривень заплатили за набори фарб?

Назва	Ціна	Кількість	Вартість
Набори олівців	5 грн.	Однакова	45 грн.
Набори фарб	8 грн.		?

1) 45 : 5 = 9 (ол.) наборів олівців;

2) 8 • 9 = 72 (к.) — заплатили за набори фарб. 232

РозділХІ. Навчання учнів розв 'язувати текстові задачі

Залежно від конкретної ситуації і поставленої мети відповіді можна давати як до початку розв'язування задачі, так і після нього. Якщо учень припустився помилки, то бажано дати йому час поміркувати, щоб він самостійно чи з допомогою вчителя знайшов правильний план розв'язування.

§38. Культура запису розв'язань задач

: Текстові задачі в початковому курсі математики розв'язують окремими діями ^без пояснення, з поясненням, за письмовим планом); способом складання виразу (без пояснення, з поясненням, готовий вираз); деякі прості задачі — способом складання рівнянь.

Розгляньмо вимоги до оформлення письмового розв'язання задач.

1-й клас. У першому класі початкової школи розв'язують тільки прості задачі. Запис розв'язання виконують у вигляді рівності, розміщеної посередині рядка.

Першокласникам іноді пропонують проілюструвати задачу малюнком. Для позначення предметів, про які йдеться в задачі, здебільшого викорис­товують кружечки, палички, трикутники, квадрати. У цьому разі розв'язання записують під малюнком (мал. 118).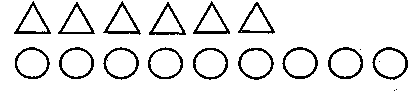



Мал. 118

2-й клас. Ще в процесі розв'язування простих задач учням варто показати, як коротко записувати задачу в один рядок, табличним способом і у вигляді структурного запису. Вони не роблять короткий запис задачі у зошиті, а розглядають його на дошці. З опорою на цей запис повторюють задачу, але розв'язання виконують так само, як і в першому класі.

Після ознайомлення зі складеною задачею діти вчаться записувати коротко задачі в зошиті, але виконують такі завдання за зразком і під керівництвом учителя. На цей час запроваджується найменування предметів у відповідях дій. Назви предметів записують однією буквою з крапкою в дужках після числа: 13 — 6 = 7 (в.). У відповідях до задачі назви предметів пишуть повністю (7 вагонів). Слова, що починаються на голосний, скорочують, як правило, до наступного голосного (яблуко — ябл., ялина — ял.). У короткому записі задач назви предметних дій (купили, продали, відрізали тощо) краще записувати повним словом. Якщо предмети, про які йдеться в задачі, відрізняються певною ознакою, то в короткому записі слід вказувати як ознаку, так і предмет. Для схематичного запису задач на знаходження суми запроваджується також фігурна дужка.

Для одного і того самого виду задач необов'язково застосовувати єдину форму короткого запису. Краще, щоб учні звикали до думки, що коротко задачу можна записувати по-різному. •■ • ■

Методика викладання математики в початкових класах

233

Задача. У бідоні міститься 9 л молока, а в каструлі — на 6л менше. Скільки літрів молока у бідоні і в каструлі разом ?

Б.-9 л.

К. — на 6 л менше.

Разом — ?

Б.-9 л.

К. — на 6 л менше.

Розв'язання задач записують окремими діями без пояснення (пояснення дають в усній формі).

1) 9 - 6 = 3 (л);

2) 9 + 3 = 12 (л). Відповідь. 12 л молока.

Застосування короткого позначення предметів може бути для дітей нелегкою справою. Тому вчитель здебільшого сам повідомляє дітям, як коротко позначити предмети у схематичному записі задачі чи в її розв'язанні.

У кінці вивчення нумерації в межах 100 ознайомлюють учнів із розв'я­занням задач складанням виразу.

У подальшій роботі вчитель сам визначає, як оформити запис розв'язання: окремими діями чи складанням виразу. Зрозуміло, що всі складені задачі з буквеними даними розв'язують складанням виразу.

Розв'язання однієї і тієї самої задачі й окремими діями, і складанням виразу практикують в окремих випадках як вид творчої роботи.

У другому півріччі запроваджують короткий запис відповіді задачі. Записують здобуте число і найменування.

У підручниках для 2-4 класів запроваджується така форма завдання, як розв'язування задач за даним планом. У 2 класі учні такий план взагалі не переписують у зошит, а учні 3 і 4 класів переписують його у зошит лише на вимогу вчителя.

3-й клас. У 3 класі учні вчаться записувати повну відповідь і короткі пояснення розв'язання. Із записом повної відповіді ознайомлюють дітей на початку навчального року. Записувати повну відповідь до кожної задачі не варто. На уроках треба практикувати як короткі, так і повні відповіді, а в домашніх і контрольних роботах повну відповідь записувати обов'язково.

Навчати коротко записувати пояснення ходу розв'язування задачі можна почати в середині першого семестру.

Задача. На 45 грн. купили набори олівців ціною по 5 грн. Стільки ж купили наборів фарб ціною по 8 грн. Скільки гривень заплатили за набори фарб?

Назва	Ціна	Кількість	Вартість
Набори олівців	5 грн.	Однакова	45 грн.
Набори фарб	8 грн.		?

1) 45 : 5 = 9 (ол.) наборів олівців;

2) 8 • 9 = 72 (к.) — заплатили за набори фарб. 234

Розділ XI. Навчання учнів розв'язувати текстові задачі

Відповідь. За набори фарб заплатили 72 грн.

Задача. З однієї грядки зрізали 8 головок капусти, а з іншої— 10. Всю капусту склали у два кошики порівну в кожний. Скільки головок капусти поклали в кожний кошик?:

Зрізали	Розклали	В один кошик
8 г.	у 2 кошики	9
10 г.

(8 + 10) (г.) капусти зрізали; (8 + 10) : 2 (г.) капусти поклали в один кошик; (8 + 10) : 2 = 9 (г.).

Відповідь. У кожний кошик поклали по 9 головок капусти. На наступних уроках учитель щоразу зазначає, як записувати розв'язання задачі: з письмовим поясненням чи записувати тільки дії і найменування їхніх результатів.

У другому півріччі варто практикувати розв'язування задач із записом

плану під керівництвом учителя. Всього так доцільно розв'язати 10—15 задач.

Задача. Школярі зобов 'язалися полагодити 180 книжок зі шкільної бібліотеки.

Першого дня вони полагодили 1/6 всіх книжок, а другого — 1/3 решти. Скільки

'книжок полагодили школярі другого дня ?

1) Скільки книжок полагодили школярі першого дня?

180:6 = 30(кн.).

2) Скільки книжок залишилося полагодити?

180-30= 150 (кн.).

3) Скільки книжок полагодили школярі другого дня?

150:3 = 50(кн.).

Відповідь. Другого дня школярі полагодили 50 книжок.

4-й клас. У 4 класі використовують ті самі форми запису розв'язання оадач, що й у 3 класі, проте іноді в короткому записі задачі за допомогою арифметичних дій визначають зв'язки, що існують між величинами. Вводиться запис розв'язання задач з письмовими формами обчислень.

Задача. Посіяли 6 кг гречки, а зібрали — в 9 разів більше. На скільки більше кілограмів гречки зібрали, ніж посіяли ?

Відомо, що посіяли 6 кг гречки. Пишемо: "Посіяли — 6 кг. Зібрали — у 9 разів більше". Це можна записати так: "Зібрали — 6'9 (кг)".

Отже, короткий запис задачі має такий вигляд:

Посіяли — 6 кг. Зібрали — (6 • 9) кг.

На скільки більше кілограмів гречки зібрали?

Щоб дізнатися, на скільки більше кілограмів гречки зібрали, ніж посіяли, треба від 6 • 9 відняти 6. Складемо вираз і обчислимо його значення:

6 • 9 - 6 = 48 (кг). Відповідь. Гречки зібрали на 48 кг більше, ніж посіяли.

Методика викладання математики в початкових класах

235

Задача. На шосе працювало 3 бригади. Перша очистила від снігу 5 км 50 м, друга — на 1км 170 м менше, ніж перша, а третя — на 150 м більше, ніж друга. Скільки метрів шосе очистили від снігу три бригади ?

І __	5 км	50 м.
II-	- на 1	км	170 м менше,	ніж	4?
III	— на	150	м більше, ніж	II.	і

_5050 1170 3880 (м) шосе очистила друга бригада;

,3880 150

4030 (м) шосе очистила третя бригада;

5050 ⁺3880 •■■': ■

4030 ;; ;_; ..

12960 (м) шосе очистили три бригади.

Відповідь. Три бригади очистили від снігу 12 км 960 м шосе.

Задача. У магазині було 5 мішків борошна по 85 кг кожен. Продали 45 кульків по 3 кг кожен. Скільки кілограмів борошна залишилося ? (Розв'язати задачу, склавши вираз, без запису пояснень).

	Було — 5 м. по 85 кг.
	Продали — 45 к. по 3 кг.
	Залишилося — ?
, 85 • 5 - 3 • 45 = 290 (кг).
1)	85 2) 45 х 5 х з	425 ■ 135

425

135

290

Відповідь. У магазині залишилося 290 кг борошна.

План розв'язування задачі є алгоритмом розв'язування даної задачі. Елементарні операції такого алгоритму — арифметичні дії. Прийом розв'язування задач за даним планом допомагає виявити, хто з учнів не оволо­дів уміннями розв'язувати ту чи іншу просту задачу, і готує молодших шко­лярів до вивчення основ інформатики. Щоб роль прийому розв'язування задач за даним планом була яскравішою, доцільно іноді план подавати у вигляді системи команд виконавцеві. Команда подається як наказове речення. 236

Розділ XI. Навчання учнів розв 'язувати текстові задачі

Задача. Господиня купила 3 кг моркви для себе і 2 кг для сусідки. За всю моркву вона заплатила 4 грн. Скільки гривень має віддати їй сусідка за моркву? Алгоритм розв'язування задачі:

а) знайти масу купленої моркви;

б) знайти ціну І кг моркви;

в) знайти вартість 2 кг моркви.

Розв'язування задачі з письмовим планом у другому півріччі можна іноді пропонувати і для домашньої роботи. Однак у контрольних роботах учні розв'язують задачі без запису плану. Щоб заощадити час, можна не записувати слова "задача", "розв'язання" чи "план розв'язування".

§39. Формування навичок розв'язувати прості задачі

Прості задачі є математичними моделями життєвих ситуацій, що вини­кають внаслідок об'єднання, вилучення чи поділу предметних множин, у процесі різницевого чи кратного порівняння двох значень тієї самої величини, а також при кількісній характеристиці якого-небудь явища кількома взаємопов'язаними величинами.

У роботі над простою сюжетною задачею йдеться про вибір тієї дії, за допомогою якої реалізується задачна ситуація. Отже, основне призначення "простих сюжетних задач — розкрити випадки застосування арифметичних дій. Тому прості задачі класифікують за характером цих випадків. Є три основні групи задач.

До першої групи належать прості задачі, під час розв'язування яких учні засвоюють конкретний зміст кожної з арифметичних дій. Це задачі на знаходження суми двох чисел, остачі, добутку, частки (ділення на рівні частини і на вміщення). Всього 5 задач.

До другої групи належать прості задачі, під час розв'язування яких учні засвоюють зв'язки між компонентами і результатами арифметичних дій. Це задачі на знаходження невідомих компонентів: доданка, зменшуваного, від'ємника, множника, діленого, дільника (8 задач).

До третьої групи належать задачі, пов'язані з поняттям різницевого чи кратного відношення двох чисел. Це задачі на збільшення чи зменшення числа на кілька одиниць або в кілька разів (у прямій і непрямій формах), на різницеве чи кратне порівняння двох чисел (12 задач).

За сюжетом у початковому курсі математики розглядають ще прості задачі на час, обчислення площі прямокутника, а також на знаходження частини числа і числа за його частиною.

Усі прості задачі, крім задач на непряме збільшення чи зменшення числа на кілька одиниць або в кілька разів, є обов'язковою складовою частиною програми.

Роль простих задач у навчанні математики надзвичайно велика. Вони служать основним засобом у формуванні поняття про арифметичні дії та величини. У процесі розв'язування простих задач учні опановують основні прийоми роботи над задачею. Високий рівень умінь розв'язувати прості задачі — необхідна умова успішного розвитку вмінь розв'язувати складені задачі.

Методика викладання математики в початковій класах

237

Навчити дітей розв'язувати задачі означає навчити їх встановлювати зв'язки між даними та шуканими величинами і відповідно до цього вибирати, а потім і виконувати арифметичні дії. Від того, наскільки добре засвоєні учнями ці зв'язки, залежить їх уміння розв'язувати задачі. Враховуючи це, у початкових класах працюють над групами задач, розв'язування яких грунтується на тих самих зв'язках між даними та шуканим, а відрізняються вони конкретним змістом і числовими даними. Групи таких задач називають задачами одного виду.

Щоб розв'язати просту задачу, учень має виділити в ній відоме і невідоме, потім вибрати арифметичну дію, за допомогою якої знайти невідоме. Для цього треба перекласти математичною мовою відношення між даними і шуканими величинами, про які йдеться в задачі, а це він зможе зробити, якщо розумітиме конкретний зміст арифметичних дій, зміст дій у поняттях "збільшити", "більше на", а також знатиме зв'язки між компонентами і результатами дій. Тому в методиці роботи над задачами одного виду виділяють три ступені. На першому ступені діти засвоюють зв'язки, на основі яких вибираються дії, на другому — вчитель ознайомлює їх з розв'язуванням задач цього виду, а на третьому — формує відповідні вміння і навички.

Зміст арифметичних дій (у широкому розумінні), зв'язки між компо­нентами і результатами дій розкривають на основі відповідних операцій над множинами предметів, повідомлення правил та ін. Отже, перший ступінь у роботі над задачами більше стосується процесу ознайомлення з матема­тичними поняттями.

Задачі на знаходження суми й остачі Ці задачі вводяться після вивчення нумерації чисел першого десятка та ознайомлення з діями додавання і віднімання. Однак цьому передує пропедевтична робота — розв'язування задач без застосування арифметичних дій, коли відповідь знаходять завдяки перелічуванню предметів або їхніх малюнків.

Особливості пропедевтичного етапу: не ставиться завдання розчленувати задачу на умову і запитання; умову задачі вчитель повідомляє здебільшого у ході виконання практичних дій чи відповідних малюнків. Запитання задачі ста­виться вже на основі виконаних дій з предметами чи за "кінцевим" малюнком.

Розгляньмо зразки такої роботи.

Задача. На годівниці спочатку було 3 горобці. Потім прилетіло 2 синиці. Скільки всього птахів стало на годівниці?

Прочитавши задачу, вчитель організовує практичну роботу дітей: "Знайдемо відповідь за допомогою кружечків. На годівниці було 3 горобці. Покладіть на парті у рядок 3 жовті кружечки. Далі сказано, що прилетіло ще 2 синички. Покладіть у цей рядок ще 2 зелених кружечки. Що означає кожен жовтий кружечок? Кожен зелений кружечок? Покажіть усіх горобців, усіх синичок, усіх птахів. Нам треба знайти, скільки стало всіх птахів на годівниці. Полічіть кружечки і дайте відповідь на запитання".

Надалі задачі на знаходження суми на пропедевтичному етапі розв'язують як на основі предметних дій, так і за малюнками. Малюнки можна виконувати як у зошитах, так і на дошці. 236

Розділ XI. Навчання учнів розв 'язувати текстові задачі

Задача. Господиня купила 3 кг моркви для себе і 2 кг для сусідки. За всю моркву вона заплатила 4 грн. Скільки гривень має віддати їй сусідка за моркву? Алгоритм розв'язування задачі:

а) знайти масу купленої моркви;

б) знайти ціну І кг моркви;

в) знайти вартість 2 кг моркви.

Розв'язування задачі з письмовим планом у другому півріччі можна іноді пропонувати і для домашньої роботи. Однак у контрольних роботах учні розв'язують задачі без запису плану. Щоб заощадити час, можна не записувати слова "задача", "розв'язання" чи "план розв'язування".

§39. Формування навичок розв'язувати прості задачі

Прості задачі є математичними моделями життєвих ситуацій, що вини­кають внаслідок об'єднання, вилучення чи поділу предметних множин, у процесі різницевого чи кратного порівняння двох значень тієї самої величини, а також при кількісній характеристиці якого-небудь явища кількома взаємопов'язаними величинами.

У роботі над простою сюжетною задачею йдеться про вибір тієї дії, за допомогою якої реалізується задачна ситуація. Отже, основне призначення "простих сюжетних задач — розкрити випадки застосування арифметичних дій. Тому прості задачі класифікують за характером цих випадків. Є три основні групи задач.

До першої групи належать прості задачі, під час розв'язування яких учні засвоюють конкретний зміст кожної з арифметичних дій. Це задачі на знаходження суми двох чисел, остачі, добутку, частки (ділення на рівні частини і на вміщення). Всього 5 задач.

До другої групи належать прості задачі, під час розв'язування яких учні засвоюють зв'язки між компонентами і результатами арифметичних дій. Це задачі на знаходження невідомих компонентів: доданка, зменшуваного, від'ємника, множника, діленого, дільника (8 задач).

До третьої групи належать задачі, пов'язані з поняттям різницевого чи кратного відношення двох чисел. Це задачі на збільшення чи зменшення числа на кілька одиниць або в кілька разів (у прямій і непрямій формах), на різницеве чи кратне порівняння двох чисел (12 задач).

За сюжетом у початковому курсі математики розглядають ще прості задачі на час, обчислення площі прямокутника, а також на знаходження частини числа і числа за його частиною.

Усі прості задачі, крім задач на непряме збільшення чи зменшення числа на кілька одиниць або в кілька разів, є обов'язковою складовою частиною програми.

Роль простих задач у навчанні математики надзвичайно велика. Вони служать основним засобом у формуванні поняття про арифметичні дії та величини. У процесі розв'язування простих задач учні опановують основні прийоми роботи над задачею. Високий рівень умінь розв'язувати прості задачі — необхідна умова успішного розвитку вмінь розв'язувати складені задачі.

Методика викладання математики в початковій класах

237

Навчити дітей розв'язувати задачі означає навчити їх встановлювати зв'язки між даними та шуканими величинами і відповідно до цього вибирати, а потім і виконувати арифметичні дії. Від того, наскільки добре засвоєні учнями ці зв'язки, залежить їх уміння розв'язувати задачі. Враховуючи це, у початкових класах працюють над групами задач, розв'язування яких грунтується на тих самих зв'язках між даними та шуканим, а відрізняються вони конкретним змістом і числовими даними. Групи таких задач називають задачами одного виду.

Щоб розв'язати просту задачу, учень має виділити в ній відоме і невідоме, потім вибрати арифметичну дію, за допомогою якої знайти невідоме. Для цього треба перекласти математичною мовою відношення між даними і шуканими величинами, про які йдеться в задачі, а це він зможе зробити, якщо розумітиме конкретний зміст арифметичних дій, зміст дій у поняттях "збільшити", "більше на", а також знатиме зв'язки між компонентами і результатами дій. Тому в методиці роботи над задачами одного виду виділяють три ступені. На першому ступені діти засвоюють зв'язки, на основі яких вибираються дії, на другому — вчитель ознайомлює їх з розв'язуванням задач цього виду, а на третьому — формує відповідні вміння і навички.

Зміст арифметичних дій (у широкому розумінні), зв'язки між компо­нентами і результатами дій розкривають на основі відповідних операцій над множинами предметів, повідомлення правил та ін. Отже, перший ступінь у роботі над задачами більше стосується процесу ознайомлення з матема­тичними поняттями.

Задачі на знаходження суми й остачі Ці задачі вводяться після вивчення нумерації чисел першого десятка та ознайомлення з діями додавання і віднімання. Однак цьому передує пропедевтична робота — розв'язування задач без застосування арифметичних дій, коли відповідь знаходять завдяки перелічуванню предметів або їхніх малюнків.

Особливості пропедевтичного етапу: не ставиться завдання розчленувати задачу на умову і запитання; умову задачі вчитель повідомляє здебільшого у ході виконання практичних дій чи відповідних малюнків. Запитання задачі ста­виться вже на основі виконаних дій з предметами чи за "кінцевим" малюнком.

Розгляньмо зразки такої роботи.

Задача. На годівниці спочатку було 3 горобці. Потім прилетіло 2 синиці. Скільки всього птахів стало на годівниці?

Прочитавши задачу, вчитель організовує практичну роботу дітей: "Знайдемо відповідь за допомогою кружечків. На годівниці було 3 горобці. Покладіть на парті у рядок 3 жовті кружечки. Далі сказано, що прилетіло ще 2 синички. Покладіть у цей рядок ще 2 зелених кружечки. Що означає кожен жовтий кружечок? Кожен зелений кружечок? Покажіть усіх горобців, усіх синичок, усіх птахів. Нам треба знайти, скільки стало всіх птахів на годівниці. Полічіть кружечки і дайте відповідь на запитання".

Надалі задачі на знаходження суми на пропедевтичному етапі розв'язують як на основі предметних дій, так і за малюнками. Малюнки можна виконувати як у зошитах, так і на дошці. 242

Розділ XI. Навчання учнів розв 'язувати текстові задачі

Завдяки такому добору задач діти вчаться розрізняти задачі на множення і ділення та знаходити слова, що є визначальними для вибору дії. Під час вивчення табличного та позатабличного множення і ділення потрібно урізноманітнювати формулювання задач, намагаючись охопити всі випадки цих дій.

Задачі на збільшення та зменшення числа на кілька одиниць. Перш ніж розглядати задачі на збільшення або зменшення числа на кілька одиниць, учні порівнюють числа, збільшують і зменшують числа на 1 і 2. Вони усвідомлюють зв'язки: збільшити — означає додати, зменшити — означає відняти. У плані актуалізації цих знань слід на кількох уроках проводити такі практичні вправи:

1. Покласти 5 паличок. Додати ще 1 паличку. Скільки паличок було спочатку? (5). Скільки паличок стало? (6). Стало більше чи менше паличок? (Більше). Яку дію виконали? (Додавання). Отже, щоб стало більше, треба додати. Можна сказати ще й так: щоб збільшити, треба додати.

До числа 5 додати 1 — це те саме, що й 5 збільшити на 1. Тому приклад 5+1 можна читати двома способами: до числа п'ять додати один і п'ять збільшити на один.

2. Покласти 5 кружечків, а паличок — стільки ж і ще 3. На скільки більше паличок буде? (На 3). Отже, це завдання можна сформулювати ще й так: покласти 5 кружечків, а паличок — на 3 більше.

3. Покласти 4 палички. Забрати 1 паличку. Скільки паличок було спочатку? (4). Скільки паличок стало? (3). Стало більше чи менше паличок? (Менше). Отже, щоб стало менше, треба відняти або, щоб зменшити, треба відняти.

4. Поклали 6 червоних паличок і стільки ж зелених. Потім 2 зелені палички забрали. На скільки менше стало зелених паличок, ніж червоних? (На 2). Отже, це завдання можна сформулювати так: покласти 6 червоних паличок, а зелених — на 2 менше.

З наведених вправ видно, що під час розв'язування задач на збільшення та зменшення числа на кілька одиниць використовують зв'язки, обернені до тих, на яких грунтується знаходження суми або остачі. Справді, задачу на знаходження суми розв'язують на основі таких міркувань: якщо додаємо, то стає більше, а при розв'язуванні задачі на збільшення числа на кілька одиниць використовують зворотний зв'язок: щоб стало більше, треба додати.

Перші дві-три текстові задачі на збільшення або зменшення числа на кілька одиниць слід розв'язувати, спираючись на малюнки або схематичні записи.

Задача. На верхній полиці 6 чашок, а на нижній — на 2 більше. Скільки чашок на нижній полиці (мал. 120)?

Мол. 120

Методика викладання математики в початкових класах

243

Розгляньте малюнок. Скільки всього чашок стоїть на верхній полиці? (Відповідь). На малюнку видно закриту полицю, де стоїть стільки чашок, скільки і на верхній полиці, тобто 6 чашок. Крім них, на цій полиці стоять ще 2 чашки. Отже, на нижній полиці стоїть на 2 чашки більше, ніж на верхній. Послухайте всю задачу. (Вчитель повторює задачу). З'ясуємо, скільки чашок на верхній полиці. (6 чашок). Що відомо про чашки на нижній полиці? (На нижній полиці на 2 чашки більше, ніж на верхній). Що запитується в задачі? (Скільки чашок на нижній полиці?). Яку дію треба виконати, щоб збільшити число на 2? (Дію додавання, додати число 2).

Розв'язування задач за допомогою схематичних записів дає змогу перейти потім до розв'язування таких задач за уявленням. Звернення до наочності надалі буде корисним під час порівняння задач.

Для розвитку вмінь учнів розв'язувати задачі на збільшення і зменшення числа на кілька одиниць доцільно практикувати розв'язування пар задач, які можна порівнювати між собою. Це такі задачі:

1. На збільшення числа на кілька одиниць і на знаходження суми двох чисел.

Задача 1, На стіл поклали 5 білих і 3 червоних кубики. Скільки всього кубиків поклали?

Задача 2. На стіл поклали 5 білих кубиків, а червоних — на 3 більше. Скільки червоних кубиків поклали?

Обидві задачі розв'язують дією додавання, але в першій задачі дізнаємося, скільки всього кубиків, а в другій — скільки червоних кубиків.

2. На знаходження остачі й на зменшення числа на кілька одиниць. Задача 1. У першій клітці було 9 кроликів, а в другій — на 4 кролики менше.

Скільки кроликів було в другій клітці?

Задача 2. У клітці було 9 кроликів, 4 кролики випустили на подвір 'я. Скільки кроликів залишилося у клітці?

3. На збільшення та зменшення числа на кілька одиниць.

Задача 1. У першій вазі 6 квіток, а в другій — на 2 квітки більше. Скільки квіток у другій вазі?

Задача 2. На першому кущі 6 помідорів, а на другому — на 2 помідори менше. Скільки помідорів на другому кущі?

Задачі на різницеве і кратне порівняння чисел. Задачі на різницеве порівняння розглядають наприкінці вивчення першого десятка, а на кратне порівняння — під час вивчення табличного множення і ділення. Розв'язування обох видів задач спирається на відповідні правила.

Правила порівняння чисел особливого доведення не потребують. Необхідність дії віднімання при різницевому порівнянні чисел видно безпосередньо, а ділення на вміщення відразу веде до висновку, що кратне порівняння чисел потребує дії ділення. Отже, достатньо тільки розвинути уявлення учнів. Для цього дають практичні вправи на різницеве або кратне порівняння довжин двох смужок.

Різницеве порівняння чисел. Первинне ознайомлення проводять на основі практичного порівняння довжини двох смужок. У кожного учня наявні лінійка і дві паперові смужки: червона смужка завдовжки 9 см і зелена — 3 см.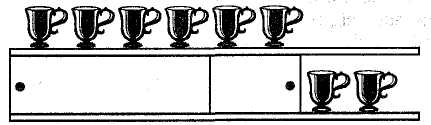



244

Розділ XI. Навчання учнів розв'язувати текстові задачі

— Дізнаємося, на скільки сантиметрів червона смужка довша від зеленої. Виміряйте довжину кожної смужки і запишіть результати вимірювання. (Учні записують у зошитах 9 см і 3 см). Як визначити, на скільки червона смужка довша від зеленої? (Учні відповідають. Учитель схвалює правильні відповіді і пропонує на червоній смужці відкласти 3 см, а потім відрізати від неї позначену частину і виміряти довжину решти смужки (6 см)). Яку дію потрібно виконати, щоб дізнатися, на скільки червона смужка довша від зеленої? (Дію віднімання).

Запишемо: 9 — 3 = 6 (см). Відповідь. На 6 см.

Чи можна сказати, на скільки зелена смужка коротша від червоної? (Також на 6 см). Отже, щоб знайти, на скільки одне число більше або менше від іншого, треба від більшого числа відняти менше.

Для закріплення діти виконують такі вправи:

1. На скільки число 6 менше від кожного з чисел: 10, 7, 8, 9?

2. На скільки число 9 більше від кожного з чисел: 6, 4, 1, 2, 5?

3. Як можна за рівністю 8 — 5 = 3 прочитати результати порівняння чисел 3 і 5? (8 більше від 5 на 3 або 5 менше від 8 на 3).

Задачу на різницеве порівняння чисел розглядають у зіставленні із задачею на збільшення числа на кілька одиниць. Надалі розв'язування задач на різницеве порівняння чергують з розв'язуванням інших простих задач, ; а згодом і складених.

Задачі на збільшення чи зменшення чисел у кілька разів. Поняття збільшення чи зменшення числа в кілька разів розкривають на основі таких завдань: І) Розгляньте малюнок і прочитайте записи (мал. 121). 2 см

- '•Мал. 121

Відрізок КМ у 4 рази довший за АВ. Скільки сантиметрів становить довжина відрізка КМ? ■■: 2-4 = 8(см).

Відповідь. КМ = 8 см.

Щоб збільшити у 4 рази, треба помножити на 4.

2) Прочитайте записи, розгляньте малюнок і поясніть розв'язання (мал. 122).

Методика викладання математики в початкових класах

245

Друга смужка у 3 рази коротша від першої. Скільки сантиметрів становить довжина другої смужки? -

9:3 = 3 (см). Відповідь. З см.

Щоб зменшити у 3 рази, треба поділити на 3. 3) Розгляньте малюнок (мал. 123).

■ ОО 00 00 СЮ 00

Мал. 123

За цим малюнком складемо задачу.

Задача. Учень намалював 2 чорних кружечки, а потім по 2 білих кружечки 5 разів. Скільки білих кружечків намалював учень ?

Цю задачу можна сформулювати й по-іншому.

Учень намалював 2 чорних кружечки, а білих — у 5 разів більше. Скільки білих кружечків намалював учень ?

Щоб дізнатися, скільки білих кружечків учень намалював, треба по 2 взяти 5 разів, тобто 2 помножити на 5. Отже, якщо сказано, що "в 5 разів більше", то треба число помножити на 5. Запишемо: 2 • 5=10.

Якщо білих кружечків у 5 разів більше, ніж чорних, то чорних кружечків у 5 разів менше, ніж білих. Складемо таку задачу.

Задача. Білих кружечків було 10, а чорних — у 5 разів менше. Скільки білих кружечків намалював учень ?

Яку дію треба виконати, щоб дізнатися, скільки було чорних кружечків? (Дію ділення). Щоб зменшити у 5 разів, треба число поділити на 5. Запишемо: 10 : 5 = 2.

З метою закріплення знань на цьому уроці дають такі практичні вправи:

а) покладіть зліва 4 квадрати, а справа — 3 рази по 4 квадрати, тобто у З рази більше. Як знайти, скільки квадратів поклали справа?

б) покладіть у верхньому рядку 8 кружечків, у нижньому — в 4 рази менше. Яку дію треба виконати, щоб зменшити в 4 рази? (Поділити 8 на 4). Скільки кружечків треба покласти у нижньому рядку?

На наступних уроках учні розв'язують текстові задачі (разом з учителем і самостійно).

Задача. У зоопарку 6 білих лебедів, а чорних — у 3 рази менше. Скільки чорних лебедів у зоопарку?

Про що треба дізнатися в задачі? Що відомо про чорних лебедів? Про білих? Чи можемо визначити, скільки чорних лебедів? Якою дією? Чому дією ділення? (Щоб зменшити у 3 рази, треба поділити на 3).

Надалі доцільно практикувати порівняння задач на збільшення числа в кілька разів і на кілька одиниць.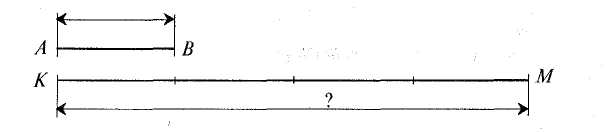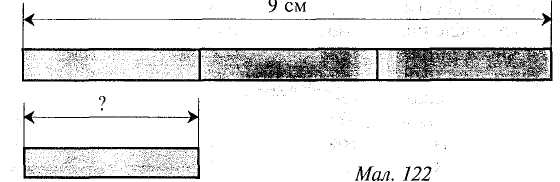







246

РозділXI. Навчання учнів розв 'язувати текстові задачі

Кратне порівняння чисел. Спочатку учні виконують завдання за підруч­ником.

Розгляньте малюнки і прочитайте запис (мал. 124).

КМ = 10 см Мал. 124

Поділимо 10 на 2: 10:2 = 5 (разів).

Відрізок АВ вмістився у відрізку КМ 5 разів.

Відрізок АВ у 5 разів коротший за відрізок КМ.

Відрізок КМ у 5 разів довший за відрізок АВ.

Потім проводять практичну роботу на порівняння довжин двох смужок. У кожного учня по дві смужки: синя смужка завдовжки 12 см і біла — 4 см.

Знайдемо, у скільки разів синя смужка довша від білої. Виміряйте довжину кожної смужки і запишіть результати. Як дізнатися, у скільки разів синя ■ смужка довша від білої? (Учні відповідають). Відкладіть білу смужку на синій, позначаючи щоразу довжину білої смужки олівцем. Скільки разів вмісти­лася біла смужка на синій? (З рази). Отже, синя смужка довша за білу в 3 рази.

Яку треба виконати дію, щоб знайти, у скільки разів число 12 більше, ніж число 4? (Дію ділення). Запишіть: 12:4 = 3. Відповідь. У 3 рази.

Якщо синя смужка у 3 рази довша, то біла — у 3 рази коротша, ніж синя.

Висновок. Щоб знайти у скільки разів одне число більше або менше від іншого, треба більше число поділити на менше.

Вправи на закріплення:

1. У скільки разів число 5 менше від кожного з чисел: 10, 30, 35?

2. У скільки разів число 24 більше від кожного з чисел: 8, 6?

3. Як можна прочитати результат порівняння чисел 6 і 18 за рівністю: 18 : 6 = 3? (18 більше від 6 у 3 рази або 6 менше від 18 у 3 рази). Робота над текстовими задачами цього виду проводиться в такому самому

плані, як при введенні текстової задачі на різницеве порівняння чисел.

Задачі на знаходження невідомого компонента арифметичної дії. Вперше із задачами на знаходження невідомого компонента учні ознайомлюються в 1 класі. Першими розглядають задачі на знаходження невідомого доданка. Зміст задачі здебільшого подають за допомогою малюнка, що наближає методику роботи над задачею до розгляду вправи на склад числа.

Задачі на знаходження невідомого доданка, зменшуваного і від'ємника розв'язують на основі конкретного змісту дій додавання і віднімання. У З класі ці задачі, а також задачі на знаходження невідомого множника, діленого і дільника розв'язують як арифметичним способом, так і скла-

Методика викладання математики в початкових класах

247

данням рівняння. Розв'язування задач арифметичним способом має велике значення для закріплення знань учнів про зв'язки між компонентами і результатом дій, дає їм змогу відчути "зворотний" хід розв'язування. Надалі діти розв'язуватимуть арифметичним способом складені задачі, що містять прості задачі на знаходження невідомого компонента дії.

Ознайомленню з кожною задачею на знаходження невідомого компонен­та дій першого ступеня передує виконання відповідних операцій над предметними множинами.

Задача. У коробці було 5 зелених і кілька червоних кружечків. Всього 8кружечків. Скільки червоних кружечків було в коробці?

На дошці запис:

Покладемо в коробку червоні й зелені кружечки. Скільки всього кружечків у коробці? (8). Скільки зелених кружечків у коробці? (5). Візьмемо з коробки зелені кружечки. Які кружечки залишилися в коробці? (Червоні).

Було 8 кружечків, 5 кружечків взяли, отже, червоних кружечків залиши­лось 8 без 5. Як дізнатися, скільки червоних кружечків було? (Треба від числа 8 відняти 5). Запишемо і виконаємо дію: 8 — 5 = 3 (к.).

Відповідь. З червоних кружечки.

Задачі на знаходження невідомого зменшуваного і від'ємника.

Задача. У коробці лежали олівці. Коли дівчинка взяла 7 олівців, то в коробці їх залишилося 18. Скільки олівців було в коробці?

Скільки олівців у коробці залишилося? (18). Скільки стане олівців, коли дівчинка покладе в коробку ті олівці, які вона взяла? (25). Як ви дізналися, що 25 олівців? (Треба до числа 18 додати 7). Запишемо розв'язання: 18 + 7 = 25. Відповідь. 25 олівців.

Задача. На столі лежало 50 зошитів. Частину цих зошитів роздали учням, після чого залишилося 32 зошити. Скільки зошитів роздали учням?

На столі було 50 зошитів. Частину роздали, а частина залишилася. Скільки залишилось? (32 зошити). Було 50 зошитів, а залишилось 32 зошити. Що зробили з рештою зошитів? (Роздали учням). Роздали не всі 50 зошитів, а без 32, які залишились. Як розв'язати задачу? (Треба від числа 50 відняти 32). Запишемо: 50 - 32 = 18 (з.). Відповідь. Роздали 18 зошитів.

Задачі на знаходження невідомого діленого.

Задача. У бідоні було молоко. Його розлили в банки по Зл кожна. Було наповнено 11 банок. Скільки літрів молока було в бідоні?

Все молоко розлили в банки. По скільки літрів молока наливали в кожну банку? (По 3 л). Скільки банок наповнили? (11 банок). Можна сказати, що ми виконали дію ділення: молоко розлили по 3 л й отримали 11 банок. У цій дії дільник 3, частка 11, а ділене — шукана кількість молока. Як знайти невідоме ділене? Запишіть розв'язання: 3 • 11 = 33 (л). Відповідь. 33 літри.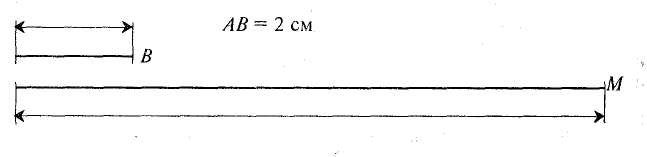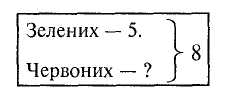





248

Розділ XI. Навчання учнів розв'язувати текстові задачі

Надалі задачі на знаходження невідомого компонента також розв'язують на основі аналізу життєвої ситуації, але можна поступово включати опору на взаємозв'язки між компонентами і результатами арифметичних дій. Якщо такий зв'язок буде сформульовано у вигляді правил, то аналіз розв'язання задач варто проводити на основі цих правил.

У 3 класі учні ознайомлюються з правилами знаходження невідомого множника, діленого і дільника, навчаються розв'язувати відповідні рівняння і застосовувати їх до задач абстрактного змісту.

Задача. Яке число треба поділити на 8, щоб отримати 2?

Позначимо шукане число буквою х. Якщо х поділити на 8, то матимемо 2. Складемо рівняння: х: 8 = 2. Тут невідомим є ділене. Щоб знайти ділене, треба дільник помножити на частку. Запишемо: х = 8 • 2, х = 16. Перевіримо: 16:8 = 2.