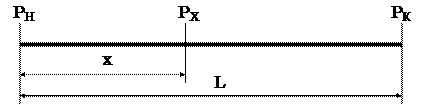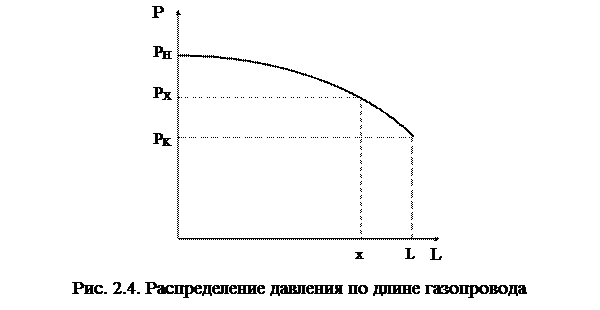аыаыа. Назначение и устройство трубопроводов, технология перекачки нефти и газа по магистральным трубопроводам
 Скачать 1.74 Mb. Скачать 1.74 Mb.
|
|
Перекачка с термообработкой Термообработка – нагрев нефти для изменения реологических параметров. Суть заключается в том, что нефть подвергается нагреву до определенной температуры, затем охлаждается с некой скоростью. Температура нагрева и скорость остывания подбираются для каждого сорта нефти отдельно. В результате резко снижаются вязкость и температура застывания. Если требуемые параметры сохраняются существенное время (одни нефти сохраняют свойства 3 дня, другие – 20 суток), то можно производить перекачку, используя данный метод. На сегодняшний день термообработка используется на магистральном нефтепроводе в Индии. Перекачка заранее нагретых нефтей Данный метод является наиболее универсальным. При этом нефть подогревается на головной нефтеперекачивающей станции, затем по всей трассе через каждые 25-100 км устанавливаются промежуточные станции подогрева. В мире эксплуатируется свыше 60 магистральных трубопроводов, по которым перекачивается нагретая нефть. Перекачка нефтей с присадками Применение нефтерастворимых присадок является распространенным способом в нашей стране. Молекулы присадок адсорбируются на поверхности кристаллов парафина, мешая их росту. Появляется суспензия парафина с огромным количеством маленьких кристаллов и высокой степенью дисперсности. При добавлении присадок нефть первоначально нагревают до полного растворения парафина, после чего нет необходимости в подогреве нефти на промежуточных станциях [2]. Самым распространенным способом является горячая перекачка. Нефть нагревается на головном пункте и закачивается в магистраль. Примерно через каждые 20 – 100 километров на трассе установлены тепловые станции, где остывшая нефть опять нагревается. Технологический расчет магистральных газопроводов Основные физические и термодинамические свойства газов. Физические свойства газа: Плотность (кг/м3). Динамическая вязкость (Па*с). Кинематическая вязкость (м2/с). Теплоемкость (Дж/К). Удельная массовая теплоемкость газа. Термодинамические свойста газа: Как известно, уравнение состояния устанавливает функциональную связь между давлением Р, объемом V, температурой T и числом молей ν газа в состоянии равновесия. Самым простым и известным уравнением состояния является уравнение состояния идеального газа PV = νRT . (3.7.1) … … С учетом этих соображений уравнение состояния идеального газа преобразуется в уравнение Ван-дер-Ваальса Основные газовые законы, уравнения состояния. Газовые законы: Уравнение состояния идеального газаопределяет связь температуры, объема и давления тел. Позволяет определить одну из величин, характеризующих состояние газа, по двум другим (используется в термометрах); Определить, как протекают процессы при определенных внешних условиях; Определить, как меняется состояние системы, если она совершает работу или получает тепло от внешних тел. Уравнение Менделеева-Клапейрона (уравнение состояния идеального газа) 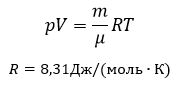 - универсальная газовая постоянная, R = kNA Уравнение Клапейрона (объединенный газовый закон) 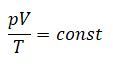 Частными случаями уравнения являются газовые законы, описывающие изопроцессы в идеальных газах, т.е. процессы, при которых один из макропараметров (T, P, V) в закрытой изолированной системе постоянный. Количественные зависимости между двумя параметрами газа одной и той же массы при неизменном значении третьего параметра называют газовыми законами. Закон Бойля – Мариотта Газ ведет себя подобно сжатой пружине, в этом можно убедиться, сжимая воздух в обычном велосипедном насосе. Бойль изучал изменение давления газа в зависимости от объема при постоянной температуре. Процесс изменения состояния термодинамической системы при постоянной температуре называют изотермическим. Произведение давления газа данной массы на его объем постоянно, если температура не меняется pV = const  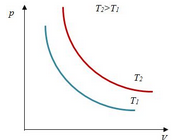  Закон Гей-Люссака Закон, определяющий зависимость объема газа от температуры при постоянном давлении (и неизменной массе). Относительное изменение объема газа данной массы при постоянном давлении прямо пропорционально изменению температуры V = V0 αT 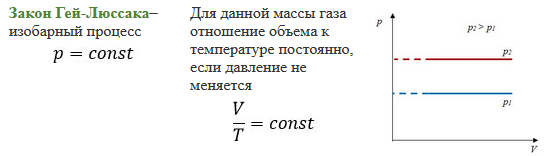 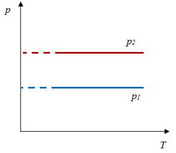 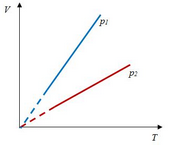 Закон Шарля Зависимость давления газа от температуры при постоянном объеме. Давление данной массы газа при постоянном объеме прямо пропорционально абсолютной температуре. p = p0 γT  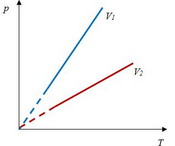 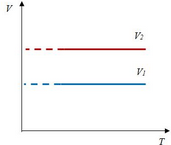 Уравнения, описывающие движение газа в трубопроводе Запишем уравнение Бернулли в дифференциальной форме: 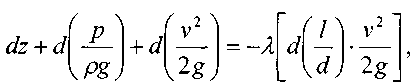 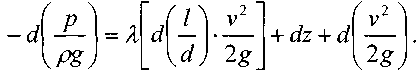 Последний член уравнения весь мал и его величиной можно пренебречь, тогда для горизонтального газопровода (z = const ) можно записать: 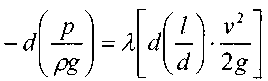 Подставив в последнее уравнение значение средней скорости движения газа, выразив её через массовый расход, получим: 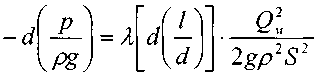 По принятым выше условиям процесс движения газа по газопроводу является изотермическим, тогда подставив в последнее уравнение значение из уравнения Бойля-Мариотта: , получим: 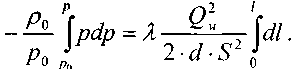 Решая последнее уравнение, получим основные расчётные формулу для определения потерь давления в газопроводе и формулу для определения массового расхода газа в газопроводе. 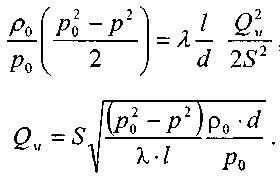 > >Величина коэффициента трения Л определяется по формулам для жидкости в зависимости от режима её движения или же можно воспользоваться эмпирической формулой: * где d- диаметр газопровода в сантиметрах. Основные формулы для гидравлического расчета магистральных газопроводов Движение газа в трубопроводе описывается, как известно из газодинамики, уравнениями: 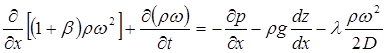 (2.1) (2.1)Первое из них называется уравнением движения, второе – уравнением неразрывности. Обозначения: – координата, совпадающая с осью трубы и направленная по течению газа; , и– соответственно плотность, линейная скорость и давление газа в сечении х (средние значения); – время; – поправочный коэффициент на неравномерное распределение скоростей по сечению; за малостью влияния его можно не учитывать (при турбулентном течении =0,02–0,03); – высота, на которой находится центр сечения , – ускорение свободного падения; – коэффициент гидравлического сопротивления; – диаметр трубопровода, принимаемый постоянным, не зависящим от х; – массовая скорость. Уравнение движения выводится из закона изменения количества движения для потока сжимаемой среды. Первый член в левой части этого уравнения характеризует интенсивность изменения количества движения по длине трубопровода, определяется разностью между выносимым через сечение , и вносимым через сечение количествами движения (через сечение в единицу времени поступает количество движения Члены, стоящие в правой части уравнения, определяют проекции на ось сил, действующих на элементарную массу газа : сил давления 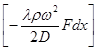 . Знак минус у этих сил обусловлен тем, что градиент давления – отрицательная величина, так как давление по длине трубопровода уменьшается, а сила трения и проекции на ось силы тяжести действуют в направлении, противоположном направлению оси . . Знак минус у этих сил обусловлен тем, что градиент давления – отрицательная величина, так как давление по длине трубопровода уменьшается, а сила трения и проекции на ось силы тяжести действуют в направлении, противоположном направлению оси . В левой части уравнения неразрывности представлена разность между количествами газа, прошедшего за единицу времени через сечения и , а в правой – накопление газа за то же время в элементарном объеме . Если через сечение вышло больше газа, чем поступило через сечение , то накопление в объеме должно быть отрицательным. Этим объясняется знак минус в правой части уравнения неразрывности. К уравнениям (2.1) и (2.2) добавляется еще уравнение состояния Рассмотрим установившееся течение газа в трубопроводе. Такой режим движения газа принимают при решении целого ряда практических задач, в том числе и при технологическом расчете магистрального газопровода. Для установившегося течения уравнения (2.1) и (2.2) упрощаются, так как пропадают члены, содержащие время. Получим Из (2.4) видно, что — постоянная величина. Поэтому d(ρω2) =ρωdω=ρω2/2. Учитывая это, приходим к известному уравнению Это уравнение говорит о том, что падение давления в трубопроводе складывается из падения давления на трение, на подъем газа по вертикали и на возрастание скорости. Уравнение (2.5) — исходное для вывода основных формул гидравлического расчета газопроводов. Чтобы получить эти формулы, следует из (2.5) исключить переменные ρ и . Это достигается при помощи уравнения неразрывности, которое запишем в виде: ( — массовый расход), и уравнения состояния 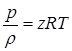 (2.7) (2.7)Температуру принимают постоянной. Коэффициент , учитывающий отклонение от законов идеального газа, также считают постоянным, поскольку он в диапазоне обычных для газопроводов условий изменяется мало. Заменив в (5.6) согласно (5.7) и (5.8) на и на и далее после интегрирования 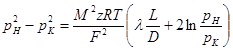 где L — длина расчетного участка газопровода, начало и конец которого обозначены индексами «н» и «к». Второе слагаемое в скобках (2lnрн/рк), учитывает возрастание кинетической энергии по длине трубопровода. Для магистральных газопроводов эта величина по сравнению с λL/D весьма мала. Пренебрегая ею и заменив F на πD2/4, получим По этой формуле можно определить падение давления в трубопроводе, если задан массовый расход М. Если расход М — искомая величина, то из (5.9) получаем Здесь должны быть заданы давления рH и рк. Разумеется, что остальные величины, входящие в (5.9) или (5.10), также должны быть известны. Формулу (5.10) называют уравнением или формулой расхода, формулу (5.9) – формулой падения квадрата давления. В проектных и эксплуатационных организациях определяют, как уже было сказано, коммерческий расход Q, т. е. объемный расход, приведенный к стандартным условиям. Заменим в (5.10) М на Q: М = Qρст. Плотность при стандартных условиях выразим в виде ρст= pст/RTст, а газовую постоянную R — через газовую постоянную воздуха и относительную плотность Δ : R = Rвозд/Δ. После таких замен получим, что коммерческий расход где Формула для разности квадратов давлений примет вид Входящие в эти формулы z, Т и подлежат предварительному определению. Вычислим, чему равен коэффициент К. Имеем: температура Тст = 293 К, давление рст= 101,3*103 Па, газовая постоянная воздуха Рвозд= 287 м2/(с2*К). Следовательно, Распределение давления по длине газопровода.
Рассмотрим участок газопровода протяженностью L, с давлением в начале PН и конце участка PК (рис 2.3) Рис. 2.3. Расчетная схема газопровода Если газопровод не имеет сбросов и подкачек, то массовый расход газа в нем неизменен. На этом основании можно записать  , (2.32) , (2.32)откуда следует 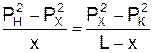 , (2.33) , (2.33)где x, PX – соответственно расстояние от начального пункта газопровода до произвольного сечения и давление в этом сечении. Освобождаясь от знаменателей и решая (2.33) относительно Px, получим формулу распределения давления по длине газопровода 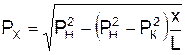 . (2.34) . (2.34)Зависимость (2.33) является уравнением параболы (рис. 2.4). По мере удаления от начала газопровода, интенсивность падения давления возрастает. Это объясняется тем, что с понижением давления уменьшается плотность газа. В соответствии с уравнением неразрывности, при уменьшении плотности газа увеличивается скорость его движения, то есть возрастают потери на трение и, следовательно, возрастает гидравлический уклон. Таким образом, потери давления на трение пропорциональны квадрату скорости газа.
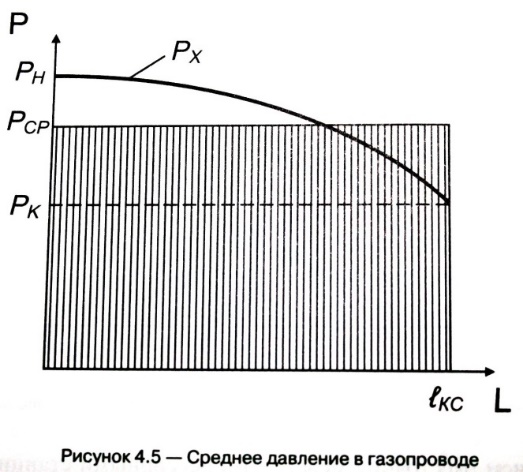
Подставив, получаем: 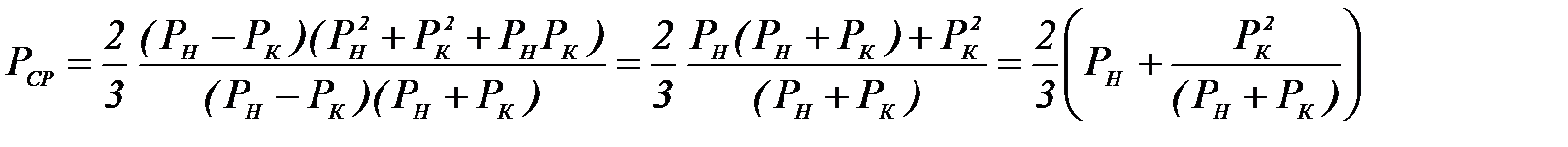 Среднее давление газа в газопроводе Среднее давление газа в газопроводе необходимо для определения его физических характеристик, а также для нахождения количества газа, заключенного в объеме трубопровода. Поскольку изменение давления по длине газопровода происходит по закону параболы (рис. 4.5), то среднее давление необходимо определять как его среднеинтегральное значение.
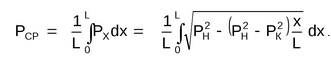 После интегрирования получаем: 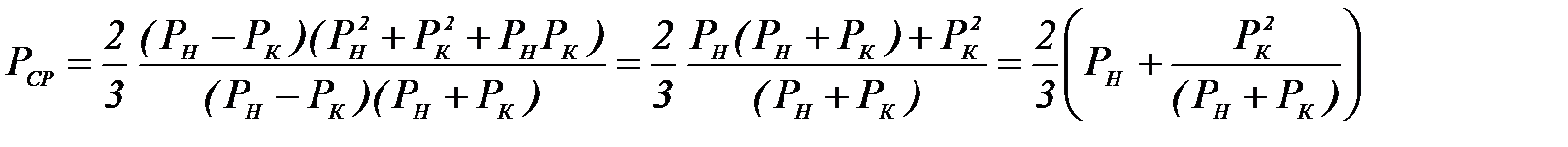 Увеличение производительности газопровода. Задача повышения пропускной способности МГ может появиться при округлении числа КС в меньшую сторону в процессе проектирования газопровода. При эксплуатации МГ необходимость повышения пропускной способности возникает в связи с ростом потребления газа или открытием нового месторождения в пределах существующего газопровода. Повышения пропускной способности можно добиться снижением гидравлического сопротивления линейной части или повышением количества энергии, передаваемой ГПА газу. Исходя из этого, возможны три способа увеличения пропускной способности МГ: - прокладкой лупинга; - удвоением числа КС; -изменением рабочих давлений в газопроводе; - комбинированный метод. При увеличении производительности газопровода меняется режим работы ГПА и КС в целом. Без расширения или реконструкции КС повышение производительности будет сопровождаться снижением степени сжатия ГПА и повышением потребляемой ими мощности. Снижение степени сжатия снижает эффект от мероприятий по увеличению пропускной способности. Возможность повышения потребляемой мощности ограничена располагаемой мощностью ГПА. С учетом этих факторов, возможность повышения производительности МГ без реконструкции компрессорных станций не превышает 5-10%. Выбор метода увеличения пропускной способности газопровода, в конечном счете, определяется экономическим сравнением технически возможных вариантов. Стоимость строительства одной КС соизмерима со стоимостью сооружения 40-80 километров трубопровода, что позволяет предположить экономическую целесообразность использования удвоения числа КС при необходимости повышения пропускной способности на величину соизмеримую с возможностями этого метода. Удвоение числа КС Эффект от удвоения числа КС будем оценивать увеличением производительности, которая определяется соотношением: 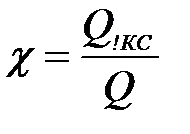 , (1.116) , (1.116)где После удвоения числа КС величина расхода составит 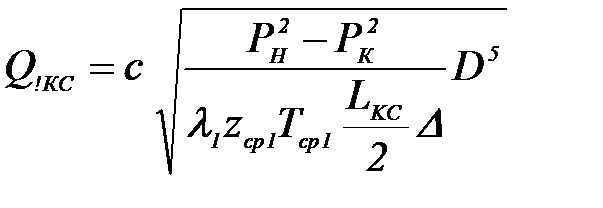 Поделив почленно полученную формулу на 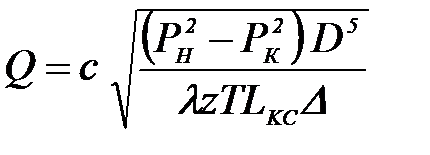 и полагая, что и полагая, что 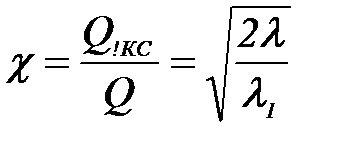 . .При квадратичном режиме течения |