статистика. Назовите и определите 3 смысла слова статистика Статистика (status состояние или положение)

• Название: Назовите и определите 3 смысла слова статистика Статистика (status состояние или положение)
• Анкор: статистика.docx
• Дата: 12.07.2018
• Размер: 224.21 Kb.
• Имя файла: статистика.docx
• Тип: Документы; #21404
• страница: 3 из 4

38.

Правило мажорантности средних:

Правило мажорантности средних : чем выше показатель степени m, тем больше величина средней.



39.Средняя величина – это обобщающий показатель, характеризующий типический уровень явления. Он выражает величину признака, отнесенную к единице совокупности.

Средняя всегда обобщает количественную вариацию признака, т.е. в средних величинах погашаются индивидуальные различия единиц совокупности, обусловленные случайными обстоятельствами. В отличие от средней абсолютная величина, характеризующая уровень признака отдельной единицы совокупности, не позволяет сравнивать значения признака у единиц, относящихся к разным совокупностям. Так, если нужно сопоставить уровни оплаты труда работников на двух предприятиях, то нельзя сравнивать по данному признаку двух работников разных предприятий. Оплата труда выбранных для сравнения работников может быть не типичной для этих предприятий. Если же сравнивать размеры фондов оплаты труда на рассматриваемых предприятиях, то не учитывается численность работающих и, следовательно, нельзя определить, где уровень оплаты труда выше. В конечном итоге сравнить можно лишь средние показатели, т.е. сколько в среднем получает один работник на каждом предприятии. Таким образом, возникает необходимость расчета средней величины как обобщающей характеристики совокупности.

Вычисление среднего – один из распространенных приемов обобщения; средний показатель отрицает то общее, что характерно (типично) для всех единиц изучаемой совокупности, в то же время он игнорирует различия отдельных единиц. В каждом явлении и его развитии имеет место сочетание случайности и необходимости. При исчислении средних в силу действия закона больших чисел случайности взаимопогашаются, уравновешиваются, поэтому можно абстрагироваться от несущественных особенностей явления, от количественных значений признака в каждом конкретном случае. В способности абстрагироваться от случайности отдельных значений, колебаний и заключена научная ценность средних как обобщающих характеристик совокупностей.

Для того, чтобы средний показатель был действительно типизирующим, он должен рассчитываться с учетом определенных принципов.

Остановимся на некоторых общих принципах применения средних величин.

1. Средняя должна определяться для совокупностей, состоящих из качественно однородных единиц.

2. Средняя должна исчисляться для совокупности, состоящей из достаточно большого числа единиц.

3. Средняя должна рассчитываться для совокупности, единицы которой находятся в нормальном, естественном состоянии.

4. Средняя должна вычисляться с учетом экономического содержания исследуемого показателя.

40.Ряд распределния является одним из видов группировок.

Ряд распределения — представляет собой упорядоченное распределение единиц совокупности по возрастающим или убывающим значениям признака и подсчет числа единиц с одним и тем же значением признака.

В зависимости от признака, положенного в основу образования ряда распределения различают атрибутивные и вариационные ряды распределения:

Атрибутивными — называют ряды распределения , построенные по качественным признакам.

Ряды распределения , построенные в порядке возрастания или убывания значений количественного признака называются вариационными.

Формы вариционного ряда:

Ранжированный ряд – это перечень отдельных единиц совокупности в порядке возрастания (убывания) изучаемого признака.

Дискретный ряд – представляет собой таблицу, состоящую из двух граф или строк: конкретных значений признака и числа единиц совокупности

Интервальный ряд – представляет собой таблицу,состоящую из двух граф или строк: интервалов признака, вариация которого изучается, и числа единиц совокупности,попадающих в данный интервал(частот), или долей этого числа от общей численности совокупности(частостей)

42.

Частота – численности отдельных вариант или каждой группы вариационного ряда n-i

43.

Накопленные частоты (обозначаются S) показывают, сколько единиц совокупности имеют значение признака не больше, чем рассматриваемое, и определяются последовательным суммированием частот интервалов. При построении кумуляты интервального ряда распределения нижней границе первого интервала соответствует частота, равная нулю, а верхней границе — частота данного интервала.

44.

Частость - частота, выраженная в долях единицы или в процентах к итогу.

45.

F - критерий Фишера является параметричесикм критерием и используется для сравнения дисперсий двух вариационных рядов. Эмпирическое значение критерия  вычисляется по формуле: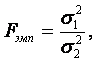



где - большая дисперсия, - меньшая дисперсия рассматриваемых вариационных рядов.

         Если вычисленное значение критерия F_эмп больше критического для определенного уровня значимости и соответствующих чисел степеней свободы для числителя и знаменателя, то дисперсии считаются различными. Иными словами, проверяется гипотеза, состоящая в том, что генеральные дисперсии рассматриваемых совокупностей равны между собой: H₀={D_x=D_y}.

         Критическое значение критерия Фишера следует определять по специальной таблице, исходя из уровня значимости α и степеней свободы числителя (n₁-1) и знаменателя (n₂-1).

         Проиллюстрируем применение критерия Фишера на следующем примере. Дисперсия такого показателя, как стрессоустойчивость для учителей составила 6,17 (n₁=32), а для менеджеров 4,41 (n₂=33). Определим, можно ли считать уровень дисперсий примерно одинаковым для данных выборок на уровне значимости 0,05.

         Для ответа на поставленный вопрос определим эмпирическое значение критерия: При этом критическое значение критерия F_кр(0,05;31;32)=2.

         Таким образом, F_эмп=1,4<2=F_кр, поэтому нулевая гипотеза о равенстве генеральных дисперсий на уровне значимости 0,05 принимается.

46.

Графическое изображение вариационных рядов

Графическое изображение зависимости между величинами дает возможность представить эту зависимость наглядно. Графики могут служить основой для открытия новых свойств, соотношений и закономерностей.

Наиболее употребительными графиками для изображения вариационных рядов, т. е. соотношений между значениями признака и соответствующими частотами или относительными частотами, являются полигон, гистограмма и кумулята.

Полигон чаще всего используют для изображения дискретных рядов. Для построения полигона в прямоугольной системе координат на оси абсцисс в произвольно выбранном масштабе откладывают значения аргумента, т. е. варианты, а на оси ординат также в произвольно выбранном масштабе - значения частот или относительных частот. Масштаб выбирают такой, чтобы была обеспечена необходимая наглядность, и чтобы рисунок имел желательный размер. Далее в этой системе координат строят точки, координатами которых являются пары соответствующих чисел из вариационного ряда. Полученные точки последовательно соединяют отрезками прямой. Крайнюю "левую" точку соединяют с точкой оси абсцисс, абсцисса которой находится слева от рассматриваемой точки на таком же расстоянии, как абсцисса ближайшей справа точки. Аналогично крайнюю "правую" точку также соединяют с точкой оси абсцисс.

Учебные достижения учащихся некоторого класса по математике характеризуются данными, представленными в таблице.

Количество баллов x	1	2	3	4	5	6	7	8	9	10	11	12
Число учащихся n	1	1	2	3	4	4	6	5	3	3	2	1

     Построить полигон частот.

Решение.

     Строим точки основываясь на данных из таблицы. Полученные точки соединяем отрезками прямой. Обратите внимание на точки (0; 0) и (13; 0), расположенные на оси абсцисс и имеющие своими абсциссами числа, на 1 меньшее и большее, чем соответственно абсциссы самой левой и самой правой точек. Полигон частот изображен на рисунке.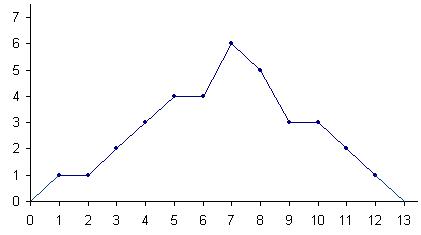



     Если полигон строят по данным интервального ряда, то в качестве абсцисс точек берут середины соответствующих интервалов. Крайние левую и правую точки соединяют с точками оси абсцисс - серединами ближайших интервалов, частоты которых равны нулю. Конечно, в этом случае полигон лишь приближенно отображает зависимость частот от значений аргумента.

Кумулята служит для графического изображения кумулятивного вариационного ряда. Для ее построения на оси абсцисс откладывают значения аргумента, а на оси ординат - накопленные частоты или накопленные относительные частоты. Масштаб на каждой оси выбирают произвольно. Далее строят точки, абсциссы которых равны вариантам (в случае дискретных рядов) или верхним границам интервалов (в случае интервальных рядов), а ординаты - соответствующим частотам (накопленным частотам). Эти точки соединяют отрезками прямой. Полученная ломаная и является кумулятой.

По данным таблицы составить кумулятивный вариационный ряд, для которого построить кумуляту.

Количество баллов x	1	2	3	4	5	6	7	8	9	10	11	12
Число учащихся n	1	1	2	3	4	4	6	5	3	3	2	1

Решение.

Cоставим кумулятивный вариационный ряд (см. таблицу ниже), для которого построим кумуляту.

Количество баллов	1	2	3	4	5	6	7	8	9	10	11	12
Частота	1	1	2	3	4	4	6	5	3	3	2	1
Накопленная частота n	1	2	4	7	11	15	21	26	29	32	34	35

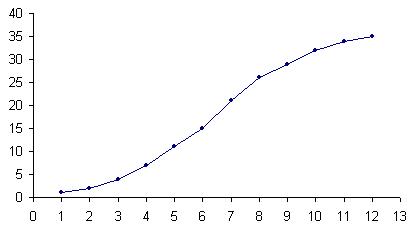Гистограмму используют для изображения интервальных рядов. Для построения гистограммы по данным вариационного ряда с равными интервалами, как и для построения полигона, на оси абсцисс откладывают значения аргумента, а на оси ординат - значения частот или относительных частот. Далее строят прямоугольники, основаниями которых служат отрезки оси абсцисс, длины которых равны длинам интервалов, а высотами - отрезки, длины которых пропорциональны частотам или относительным частотам соответствующих интервалов.

В результате получают ступенчатую фигуру в виде сдвинутых друг к другу прямоугольников, площади которых пропорциональны частотам (или относительным частотам).

Если интервалы неравные, то на оси ординат следует откладывать в произвольно выбранном масштабе значения плотности распределения (абсолютной или относительной). Таким образом, высоты прямоугольников, которые мы строим, должны равняться плотностям соответствующих интервалов.

При графическом изображении вариационного ряда с помощью гистограммы плотность изображается так, как если бы она оставалась постоянной внутри каждого интервала. На самом деле, как правило, это не так. Если построить распределение по частям интервалов, то можно убедиться в том, что плотность распределения на различных участках интервала не остается постоянной. Плотность, полученная ранее, предствляла лишь некоторую среднюю плотность. Итак, гистограмма изображает не фактическое изменение плотности распределения, а лишь средние плотности распределения на каждом интервале.

Если построена гистограмма интервального распределения, то полигон того же распределения можно получить, если соединить прямолинейными отрезками середины верхних оснований прямоугольников.

Пример:

По результатам тестирования по математике учащихся 7-го класса получены данные о доступности заданий теста (отношение числа учащихся, правильно выполнивших задания, к числу тестировавшихся учащихся), предствленные ниже, в таблице.
     Тест содержал 25 заданий. Построить гистограмму.

Доступность задания x, %	25-35	35-45	45-55	55-65	65-75	75-85	85-95
Количество задач n	1	1	5	7	7	3	1

Решение.

     Откладываем на оси абсцисс 7 отрезков длиной 10. На них, как на основаниях, строим прямоугольники, высоты которых соответственно равны 1, 1, 5, 7, 7, 3, 1. Полученная ступенчатая фигура и является искомой гистограммой.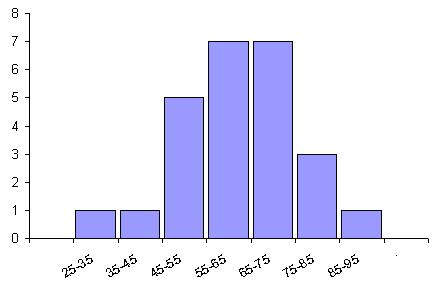



47.

Этапы изучения вариации.

1)построение вариационного ряда;

2)графическое изображение вариационного ряда, анализ графического изображения;

3)анализ вариационного ряда с помощью системы показателей.

 

48) Медиа́на — возможное значение признака, которое делит ранжированную совокупность (вариационный ряд выборки) на две равные части: 50 % «нижних» единиц ряда данных будут иметь значение признака не больше, чем медиана, а «верхние» 50 % — значения признака не меньше, чем медиана.

Медиана определяется для широкого класса распределений (например, для всех непрерывных), а в случае неопределённости, естественным образом доопределяется, в то время как математическое ожидание может быть не определено.

У интервального вариационного ряда распределения медиана принадлежит медианному интервалу и имеет определённое значение.

Для определения медианы используют накопленные частоты по которым строится кумулятивная кривая. Вершины ординат, соответствующих накопленным частотам, соединяют отрезками прямой. Разделив пополам последнюю ординату, которая соответствует общей сумме частот и проведя к ней перпендикуляр пересечения с кумулятивной кривой, находят ординату искомого значения медианы.

49)

50) Мода — значение признака, имеющее наибольшую частоту в статистическом ряду распределения. 

Нахождение моды и медианы в контрольных по статистике происходит путем обычного просматривания столбца частот. В этом столбце находят наибольшее число, характеризующее наибольшую частоту.

51) Размах вариации – это разность между наибольшим и наименьшим значением признака в изучаемой совокупности: R=x_max – x_min,

где   x_max – наибольшее значение признака;

x_min – наименьшее значение признака.

Размах вариации не отражает отклонений всех значений признака – это его недостаток. Он исчисляется при контроле качества продукции для определения систематически действующих причин на производственный процесс.

52) Дисперсия –  – определяется по формулам:

для ранжировочного ряда (несгруппировочных данных): ;

Коэффициент осцилляции – это отношение размаха вариации к средней, в процентах. Отражает относительную колеблемость крайних значений признака вокруг средней. .

Линейный коэффициент вариации характеризует долю усредненного значения абсолютного отклонения от средней величины. .

53) В итоге, средне линейное отклонение будет рассчитываться по формуле:



где

a – среднее линейное отклонение,

x – анализируемый показатель, с черточкой сверху – среднее значение показателя,

n – количество значений в анализируемой совокупности данных,

оператор суммирования, надеюсь, никого не пугает.

54) Как и среднее линейное отклонение, дисперсия также отражает меру разброса данных вокруг средней величины.

Формула для расчета дисперсии выглядит так:



где

D – дисперсия,

x – анализируемый показатель, с черточкой сверху – среднее значение показателя,

n – количество значений в анализируемой совокупности данных.

55) Первый принцип. Сравниваемые в относительном показателе абсолютные показатели должны быть чем-то связаны в реальной жизни объективно, независимо от нашего желания.

Второй принцип. При построении относительного статистического показателя сравниваемые исходные показатели могут различаться только одним атрибутом или видом признака.

Третий принцип. Необходимо знать возможные границы существования относительногопоказателя. Например, как будет показано в главе о вариации, относительные показателивариации теряют смысл и не могут применяться в тех случаях, когда их знаменатели -средниезначения признаков близки к нулю, потому что при стремлении знаменателя к нулюотносительный показатель стремится к абсурдному бесконечному значению.

56) Коэффициент эластичности показывает, на сколько процентов изменится величина результативной переменной у, если величина факторной переменной изменится на 1 %.

57) Коэффициент вариации представляет собой относительную меру рассеивания, выраженную в процентах. Он вычисляется по формуле:

,

где  - искомый показатель, - среднее квадратичное отклонение, - средняя величина.

58) В 87% случаев изменения х приводят к изменению y. Другими словами - точность подбора уравнения регрессии – высокая.

59) y€ = 425 – 5,09t – 1,59t^2

t = 10

y€= 425 – 5,09*10 – 1,59*100

y€= 215,1

60-71

60. Причины использования выборочного метода :

1. Повышение точности данных: уменьшение числа единиц наблюдения в выборке резко снижает ошибки регистрации. Правда, за счет неполноты охвата единиц возникает ошибка репрезентативности, т.е. представительности выборочных данных. Но даже взятые вместе ошибка наблюдения для выборки плюс ошибка репрезентативности обеспечивают большую точность выборочных данных по сравнению с массовым сплошным наблюдением.

2. Обращение к выборкам обеспечивает экономию материальных, трудовых, финансовых ресурсов и времени

3. Без выборки не обойтись, когда наблюдение связано с порчей наблюдаемых объектов. Это относится прежде всего к изучению качества продукции, которое основано на испытаниях образцов на вибрацию, упругость, разрыв и т.дНа выборках основаны маркетинговые исследования, оценки качества поставок.

61. Генеральная совокупность - совокупность всех единиц наблюдения, представляющая изучаемое явление.

62. Выборочная совокупность - часть объектов из генеральной совокупности, отобранных для изучения, с тем чтобы сделать заключение о всей генеральной совокупности. 
Для того, чтобы заключение, полученное путем изучения выборки, можно было распространить на всю генеральную совокупность выборка должна обладать свойством репрезентативности.

63. Репрезентативность выборки — это показатель, заключающийся в том, что выборка должна полно и достоверно отображать признаки той совокупности, частью которой она является. Её также можно определять как свойство выборки наиболее полно представлять характеристики генеральной совокупности, существенные с точки зрения цели исследования.

64. Простая случайная выборка формируется произвольным отбором элементов из основы выборки. (Этот метод похож на розыгрыш лотереи, когда таблички с именами участников помещаются в барабан, который встряхивается, и из него произвольным образом извлекают отдельные таблички, в результате объективно определяются имена победителей.)

65.задача

66.задача

67. Механическая выборка формируется так: генеральная совокупность делится на столько групп, сколько единиц наблюдения должно войти в выборку, и из каждой группы выбирается одна единица. Существует два принципиально отличных друг от друга способа формирования механической выборки: по неранжированным данным и по ранжированным данным генеральной совокупности. В первом случае результаты механического отбора по сути будут являться реализацией случайного бесповторного отбора, так как единицы наблюдения располагаются в случайном порядке. Во втором случае единицы наблюдения определенным образом упорядочиваются по величине изучаемого или коррелирующего с ним признака. В этом отборе получается более точное распределение единиц выборочной совокупности к распределению в генеральной совокупности, чем при собственно-случайном отборе. Оценка точности результатов механической выборки производится с помощью тех же формул, что и для собственно-случайной выборки.

68. Оценка значимости уравнения  регрессии в целом производится на основе F-критерия Фишера, а также с помощью t-статистика Стъюдента

69. В случае, если фактическое значение t-статистики по модулю меньше табличного, то уравнение регрессии является статистически не значимым

70. В случае, если фактическое значение F-критерия больше табличного, то уравнение регрессии является статистически зачимым и надежным

71. Малые выборки, статистические выборки столь малого объёма n, что к ним нельзя применить простые классические формулы, действующие лишь асимптотически при n ® ¥. 

№ 72.Ошибки репрезентативности (представительности) возникают в результате неполного обследования и в случае, если обследуемая совокупность недостаточно полно воспроизводит генеральную совокупность. Они могут быть случайными и систематическими. Случайные ошибки репрезентативности – это отклонения, возникающие при несплошном наблюдении из-за того, что совокупность отобранных единиц наблюдения (выборка) неполно воспроизводит всю совокупность в целом. Систематические ошибки репрезентативности – это отклонения, возникающие вследствие нарушения принципов случайного отбора единиц. Ошибки репрезентативности органически присущи выборочному наблюдению и возникают в силу того, что выборочная совокупность не полностью воспроизводит генеральную. Избежать ошибок репрезентативности нельзя, однако, пользуясь методами теории вероятностей, основанными на использовании предельных теорем закона больших чисел, эти ошибки можно свести к минимальным значениям, границы которых устанавливаются с достаточно большой точностью.

Ошибки выборки – разность между характеристиками выборочной и генеральной совокупности. Для среднего значения ошибка будет определяться по формуле :



№73.Метод наименьших квадратов (МНК, англ. Ordinary Least Squares, OLS) — математический метод, применяемый для решения различных задач, основанный на минимизации суммы квадратов некоторых функций от искомых переменных. Он может использоваться для «решения» переопределенных систем уравнений (когда количество уравнений превышает количество неизвестных), для поиска решения в случае обычных (не переопределенных) нелинейных систем уравнений, для аппроксимации точечных значений некоторой функцией. МНК является одним из базовых методов регрессионного анализа для оценки неизвестных параметров регрессионных моделей по выборочным данным.

№74

ЗП сред= [((100+180)/2)*4 + ((180+260)/2)*16+ ((260+340)/2)*10]/30=236 т.р.

№75 вопроса нет.

№76 выручка от реализации сократилась на 10 %.

№77 Полиго́н часто́т (в математической статистике) — один из способов графического представления плотности вероятности случайной величины. Представляет собой ломаную, соединяющую точки, соответствующие срединным значениям интервалов группировки и частотам этих интервалов.

Полигоном частот называют ломанную, отрезки которой соединяют точки (x1; n1), (x2; n2), ..., (xk; nk). Для построения полигона частот на оси абсцисс откладывают варианты xi, а на оси ординат - соответствующие им частоты ni. Точки ( xi; ni) соединяют отрезками прямых и получают полигон частот

№79. При увеличении дохода семьи на 1 тыс руб увеличится и количест потребляемого мяса на 0,12 кг. При изменении признака фактора х изменяется и результативный фактор.

№ 80-83


Существует два вида связи между факторами и результативными признаками: функциональная связь корреляционная связь При функциональной связи каждому значению величины факторного признака соответствует только одно значение результативного признака. Функциональные связи обычно выражаются формулами и исследуются в математике и физике. Пример, площадь круга – результативный признак – прямо пропорциональна его радиусу – факторный признак. Однако, функциональные связи имеют место и в экономике.

Пример, заработная плата рабочего повременной оплате равна произведению часовой тарифной ставки на число отработанных часов. Функциональная связь является точной и полной, т.к. обычно известны все факторы, оказывающие влияние на результативный признак. При функциональных связях величина результативного признака полностью показывается факторными признаками. Однако, в массовых явлениях общественной жизни в виду крайнего разнообразия факторов и их взаимосвязи и противоречивого действия этих факторов, не поддающихся строгому учету и контролю, возникает широкое варьирование результативного признака.

Это свидетельствует о том, что связь между признаками неполная, а проявляется лишь в общем и среднем. Такие связи называются корреляционными. При корреляционной связи под влиянием изменения многих факторных признаков (ряд из которых может быть неизвестен), меняется средняя величина результативного признака. Пример, корреляционная связь между влиянием удобрения и урожайностью культур, между производительностью и энергооснощенностью предприятия. Важная особенность корреляционных связей состоит в том, что они обнаруживаются не в отдельных случаях, а в массовых общественных явлениях. Проявление корреляционных зависимостей подвержено действию закона больших чисел: лишь в достаточно большом числе фактов индивидуальные особенности и второстепенные факты сгладятся и зависимость проявится достаточно отчетливо.

Вторая важная особенность корреляционных связей состоит в том, что эти связи неполные. Даже на массовых данных обнаруженные зависимости не будут носить полного, т.е. функционального характера. В зависимости от действия функциональных и корреляционных связей их делят на: прямые обратные

Прямая связь – направление изменения результативного признака совпадает с направлением изменения признака фактора, т.е. с увеличением факторного признака увеличивается и результативный и наоборот. Обратная связь – направление изменения результативного признака не совпадает с изменением факторного признака, т.е. при увеличении факторного признака результативный уменьшается и наоборот.

СТАТИСТИЧЕСКАЯ СВЯЗЬ [statistical interdependence] — связь между переменными, на которую накладывается воздействие случайных факторов. В результате действия такой связи изменения одной переменной приводят к изменениям другой не детерминированно, как при функциональной связи (см. Функция), а статистически, отражаясь на изменении математического ожидания последней.

84)Корреляционный анализ -раздел математической статистики, объединяющий практические методы исследования корреляционной связи между двумя и более случайными признаками или факторами.

Цель корреляционного анализа — обеспечить получение некоторой информации об одной переменной с помощью другой переменной. В случаях, когда возможно достижение цели, говорят, что переменные коррелируют.

85) Регрессионный анализ — метод моделирования измеряемых данных и исследования их свойств. Данные состоят из пар значений зависимой переменной (переменной отклика) и независимой переменной (объясняющей переменной).

86)Метод наименьших квадратов.

МНК является одним из базовых методов регрессионного анализа для оценки неизвестных параметров регрессионных моделей по выборочным данным.

Пусть дана система уравнений , где  — некоторые функции,  — некоторые известные значения, x — набор неизвестных (искомых) переменных. Для произвольных значений  значения  отличаются от . Суть метода наименьших квадратов заключается в том, чтобы найти такие значения , при которых минимизируется сумма квадратов отклонений (ошибок)  .

87 и 88 есть у нас в распечатке (тема корреляционно-регрессионный анализ и моделирование)

89) Парная корреляция - это связь между двумя показателями, один из которых является фактором, другой - результативным показателем. 

90) Множественная корреляция возникает от взаимодействия нескольких факторов с результативным показателем. 

91) Прямая связь — направление изменения результативного признака совпадает с направлением изменения признака фактора, т.е. с увеличением факторного признака увеличивается и результативный и наоборот.

Обратная связь — направление изменения результативного признака не совпадает с изменением факторного признака, т.е. при увеличении факторного признака результативный уменьшается и наоборот.

92) Совокупность однородна если Vx<33% (тоже есть в распечатке той же)

93) Нормальность исследования определяется с помощью трех сигм.

94) 1. |Rxjy|-1,то степень тесноты связи с результативным показателем значительна,

2.Rxjy>Rxjxi , то связь фактора xj с результативным признаком y теснее,чем с любым другим фактором xi

Если (2) не выполняется,то исключается фактор,связь которого с Yменее тесная.

95) Связь прямая и функциональная.

96. это говорит об обратной связи между У и X

97. говорит о том, что данные не связаны друг с другом

98. тесная связь между признаками

99. связи между данными нет

100. для исследования степени тесноты связи между качественными признаками, каждый из которых представлен в виде альтернативных признаков, может быть использован коэффициент ассоциации Д. Юла и коэффициент контингенции К. Пирсона. Расчетная таблица в этом случае состоит из четырех ячеек (таблица “четырех полей”), статистическое сказуемое которой схематически может быть представлено в следующем виде:

Признаки	А (да)		Итого
В (да)	а	Ь	а+ b
В(нет)	с	d	c+d
Итого	а + с	b+d	П

a, b. с, d — частоты взаимного сочетания (комбинации) двух альтернативных

признаков

п - общая сумма частот.

Коэффициент ассоциации исчисляется по формуле




Коэффициент контингенции:



где а. Ь. с, d - числа в четырехклеточной таблице.

Коэффициент контингенции также изменяется от -1 до +1, но всегда его величина для тех же данных меньше коэффициента ассоциации.

101. Ряд динамики – это значения статистических показателей, которые предоставлены в определенной хронологической последовательности.