статистика. Назовите и определите 3 смысла слова статистика Статистика (status состояние или положение)

Название	Назовите и определите 3 смысла слова статистика Статистика (status состояние или положение)
Анкор	статистика.docx
Дата	12.07.2018
Размер	224.21 Kb.
Формат файла
Имя файла	статистика.docx
Тип	Документы #21404
страница	2 из 4

1 2 3 4

20.Открытые – это те интервалы, у которых указана только одна граница: верхняя – у первого интервала, нижняя – у последнего. Например, до 10, свыше 20. Ширина открытого интервала принимается равной ширине смежного с ним интервала.

Закрытыми называют интервалы, у которых обозначены обе границы. 0–10, 10–20

21. Величина равного интервала определяется по формуле:

i = (Xmax — Xmin) / n

где x max , x min – наибольшее и наименьшее значения группировочного признака в совокупности,

n – число групп,

xmax – x min – размах вариации.

Полученную по формуле величину необходимо округлить. Она является шагом интервала.

22. Статистический показатель — это количественная оценка свойства изучаемого явления. В зависимости от целевой функции статистических показателей их можно подразделить на два основных вида: учетно-оценочные показатели; аналитические показатели.

23. Статистический показатель представляет собой обобщающую характеристику изучаемого объекта, в которой объединяются его качественная и количественная определенность. Признак – это объектив¬ная характеристика единицы статистической совокупности, характерная черта или свой¬ство, которое может быть определено или измерено. Например: средний размер з/п в Украине – статистический показатель, а з/п конкретного человека – признак.

24.) Классификация видов статистических показателей: основания классификации, названия и определения классов, примеры (до групп относительных показателей).

Основания классификации:

По качественной стороне показателей	По количественнойстороне показателей	По отношению кхарактеризуемому свойству
1. Показатели свойств конкретныхобъектов	1. Абсолютные	1. Прямые
2. Показатели статистических свойствлюбых массовых явлений и процессов	2. Относительные	2. Обратные

Абсолютным показателем является такой, который отражает либо суммарное число ед. ,либо суммарное свойство объекта. Например, число крестьянских хозяйств в Ленинградскойобласти на 1 января 1997 г., посевная площадь картофеля в районе, сумма средств,направленных на потребление за конкретный месяц или год, и т. п.

Абсолютные показатели, как правило, выражаются именованными величинами в натуральныхединицах измерения: тоннах, штуках, часах, амперах и т. п., в условных единицах: условномтопливе, нормо-сменах, килономерах пряжи и т. д. или в стоимостных единицах: рублях,долларах, марках. Они характеризуют сумму значений первичных признаков объекта.Совершенно понятно, что наука не может ограничиваться характеристиками толькоизолированных отдельных свойств объекта. Поэтому статистика не ограничиваетсяабсолютными показателями. Она измеряет и характеризует соотношение разных абсолютныхвеличин, их изменения во времени, их взаимосвязи между собой и окружающей средой.Статистика, как и все науки, широко пользуется общенаучными методами сравнения,обобщения, синтеза.
25.) Группы относительных показателей, примеры.

1. Относительные показатели, характеризующие структуру объекта. Это доля (удельный вес) -отношение части к целому. На-пример,отношение площади каждой из сельхоз культур к общей посевной площади; числа женщин к общей численности населения города, республики. В эту жегруппу входят характеристики отношения между отдельными частями объекта; показатели,характеризующие степень сложности структуры, степень неравномерности (вариации) долей идр. Доли выражаются нередко в процентах или промилле (тысячных долях).
2. Относительные показатели, характеризующие динамику прогресса, изменение во времени.Это отношения показателей, характеризующих объект в более позднее время (текущийпериод), к аналогичным показателям того же объекта в более ранний (базисный) период.

Такие показатели называют темпами роста. Темп роста может быть выражен в разах или в процентах.Темп роста говорит о том, во сколько раз больше .показатель текущего периода в сравнении сбазисным или сколько процентов он составляет по отношению к показателю базисного периода.К относительным показателям динамики принадлежат также темпы прироста, параметрыуравнений трендов, коэффициенты колеблемости и устойчивости в динамике, индексныепоказатели динамики.
3. Относительные показатели, характеризующие взаимосвязь признаков в совокупностиявлений, а также взаимосвязь результативных признаков-следствий с факторнымипризнаками-причинами, например, связь уровня душевого дохода с размером потребления мясаили фруктов на одного человека; связь дозы удобрений с урожайностью картофеля и т.п. К таким показателям относятся коэффициенты корреляции, эластичности, детерминации, аналитические индексы. Относительныепоказатели взаимосвязи могут быть как отвлеченными, так и именованными числами.
4. Относительные показатели, характеризующие соотношение разных признаков того же объекта между собой (иногда их называют показателями интенсивности). Эти показатели обобщают вторичные признаки объектов (например, производительность труда— отношение произведенной продукции в натуральном или стоимостном выражении к затратам труда на ее производство и др.). Показатели соотношения признаков могут быть прямыми и обратными. Например, отношение затрат труда на производство к объему продукции дает показатель трудоемкости продукции — величину, обратную прямому показателю производительности труда. И прямые, и обратные показатели выражаются именованными числами с двойнымиединицами измерения обоих сравниваемых признаков: в рублях за 1 час труда, в центнерах с 1 гаплощади. Например, продукция предприятия учитывается в миллионах рублей за год, скажем, 1800, и стоимость основных производственных фондов предприятия тоже учитывается вмиллионах рублей, т. е. 4000. Если формально единицы измерения сравниваемых признаковсовпадают, то неверно фондоотдачу - показатель сравнения стоимости продукции за год состоимостью среднегодовых производственных фондов -называть отвлеченным числом (в нашемпримере - 0,45). Правильно будет сказать «фондоотдача составила 45 коп. продукции на 1рубль основных фондов за год». Стоимость продукции и стоимость фонда - разные признаки,хотя имеют одинаковую единицу измерения.

В экономике относительные показатели, характеризующие величину признака объекта,рассчитанные на единицу другого признака, используются для измерения эффективности либоинтенсивности производства.

К данному классу показателей принадлежат и показатели, характеризующие степеньсистемности признаков, например соотношение между суммой осадков и суммой эффективныхтемператур (способствующих произрастанию сельскохозяйственных культур), так называемыйгидротермический коэффициент; таково же соотношение между весом и ростом человека,характеризующее пропорциональность его тела.
5. Особым видом относительных статистических показателей являются отношения фактическинаблюдаемых величин признака к его нормативным, плановым, оптимальным или максимальновозможным величинам. Это широко распространенные на производстве- показатели выполнениянорм выработки, норм расхода материалов и других ресурсов. Отношения наблюдаемых величинпризнака к оптимальным или плановым характеризуют приближение изучаемого процесса кидеалу. Так, если оптимальная норма потребления мяса взрослым мужчиной на Северо-ЗападеРоссии составляет 80 кг в год, а фактическое среднедушевое потребление составило в 1992 г. 58 кг, то ясно, что размер и структура потребления далеки от оптимальной: всего 72%. Всякоепревышение или недобор до оптимальной величины, всякое отклонение от 100% такогоотносительного показателя (в любую сторону) означают нарушение оптимальности процесса,даже перевыполнение плана, если план не лозунг, а научно обоснованная, взаимосвязаннаясистема объемов производства отдельных видов продукции. В этом случае превышениепланового выпуска одного вида продукции, например выплавки стали без согласованногоизменения производства станков, прокатных станов, других средств обработки металла, естьпопросту омертвление затрат и бесполезный перерасход природных ресурсов, труда.

Отношение фактических значений признака к максимально возможным значениям частохарактеризует качество процесса, агрегата, машины. Таковы, например, коэффициентыполезного действия двигателей, электромоторов. Отношения фактических показателейвариации к максимально возможным при данной численности совокупности используются прианализе вариации (см. гл. 5), при измерении степени специализации предприятия или региона напроизводстве определенной продукции и в ряде других задач.

Само задание в той или иной отрасли экономики может быть выражено относительнойвеличиной динамики или структуры. Например, «снизить затраты топлива на 1 кВт-чэлектроэнергии на 5% в сравнении с прошлым годом»; «увеличить долю продукции высшегокачества до 85% общего выпуска». Показатели выполнения такого задания будут являтьсяотносительными показателями второго порядка.
6. Еще один вид относительных статистических показателей возникает в результате сравненияразных объектов по одинаковым признакам. Сравнение урожайности одной и той же культуры втом же году между хозяйствами, областями; сравнение показателей производства или уровняжизни населения в разных странах - это обычные приемы познания. При построении такихотносительных показателей необходимо позаботиться, чтобы сравниваемые показателиопределялись по единой методике построения, были сравнимы по единицам измерения и во всехдругих отношениях. В социально-экономической статистике есть специальный раздел омеждународных сравнениях показателей.

В качестве примера приведем сравнение производства валового внутреннего- продукта на душунаселения в Великобритании и в США в 1990 г.: в Великобритании на 1 жителя былопроизведено 12715 долл., в США - 18 347 долл./чел. Показатель сравнения может бытьпостроен как отношение одного душевого уровня к другому: душевое производство ВВП вВеликобритании составило 69,3% душевого производства ВВП в США. Или душевоепроизводство ВВП в США составило 18 347: 12 715 = 1,443, или 144,3% душевого производствав Великобритании. Если речь идет об исследовании по экономике Великобритании, топредпочтительнее первая форма показателя: изучаемый объект (сравниваемая величина) -числитель, а другой объект (база сравнения) - знаменатель относительного показателя. Еслиизучается экономика США, предпочтительнее взять в числителе показатель США.
26.) Функции статистических показателей.

Познавательно-информационная функция. Без статистической информации невозможнопознание закономерностей природных и социальных массовых явлений, их предвидение, азначит, и регулирование либо прямое управление, будь то на уровне отдельного предприятия,фермера, города или региона, на государственном или межгосударственном уровне.

Прогностическая функция, т. е. роль статистических показателей в предвидении будущего, тесно связана с их информационной функцией. Конечно, данная функция присуща не всемстатистическим показателям, а тем из них, которые используются при моделировании массовых процессов.

Оценочная функция статистических показателей заключается в том, что на их основе люди,общество, государство оценивают деятельность предприятий, организаций, трудовых и творческих коллективов, правительств.

Рекламно-пропагандистская функция статистических показателей. Весьма не однозначная функция статистических показателей. Связано это с тем, что реклама - это одно из нормальных явлений рыночной экономики, и фирмы, компании, естественно, стремятся использовать в рекламе статистические показатели одолговечности, качественности своей продукции, зная, что цифровым данным люди большедоверяют, чем словам. Но при таком использовании статистических показателей велик рисклибо подмена реального показателя планируемым, т. е. желаемым, но еще не осуществленным,либо умолчание о других показателях товара, не отвечающих целям рекламы. Поэтому кстатистическим показателям, используемым в рекламных интересах, следует относиться весьмаосторожно, по возможности проводить дополнительные расчеты и анализ.

27.) Свойства массовых явлений и процессов.
Я в душе не ебу!

28.) Вариация-это…

различие значений какого-либо признака у разных единиц совокупности за один и тот же промежуток времени. Причиной возникновения вариации являются различные условия существования разных единиц совокупности.
29.) Главное значение средних величин.

Средние величины относятся к обобщающим статистическим показателям, которые дают сводную (итоговую) характеристику массовых общественных явлений, так как строятся на основе большого количества индивидуальных значений варьирующего признака.
30.) Среднее арифметическое-это…

сре́днее арифмети́ческое — одна из наиболее распространённых мер центральной тенденции, представляющая собой сумму всех наблюденных значений, деленную на их количество.
31.) Формула простой средней арифметической.

$\bar{x} = \frac{1}{n}\sum_{i=1}^n x_i = \frac{1}{n} (x_1+\cdots+x_n).$

32.) Формула взвешенной средней арифметической.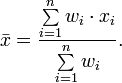
$\bar{x} = \frac{ \sum\limits_{i=1}^n w_i \cdot x_i}{\sum\limits_{i=1}^n w_i}.$

33.) Категории средних величин и виды средних, к которым они относятся.

степенные средние (средняя гармоническая, средняя геометрическая, средняя арифметическая и др.). Для вычисления степенных средних необходимо использовать все имеющиеся значения признака. Если рассчитывать все виды степенных средних для одних и тех же данных, то их значения окажутся одинаковыми. Тогда действует правило мажорантности средних: с увеличением показателя степени средних увеличивается и сама средняя величина.

структурные средние (мода, медиана). Мода и медиана определяются лишь структурой распределения. Поэтому их именуют "структурными позиционными средними". Медиану и моду часто используют как среднюю характеристику в тех совокупностях, где расчет средней степенной невозможен или нецелесообразен.
34.) Форума степенной средней степени d.

$a_d(x_1, \ldots, x_n) = \sqrt[d]{\frac{\sum\limits_{i=1}^n x^d_i}n}$
35.) Формула средней квадратической. Статистический показатель на ее основе.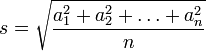
$s=\sqrt{\frac {a_1^2+ a_2^2+ \ldots+ a_n^2} {n}}$

На основе данной формулы строится такой статистический показатель как дисперсия.

36.

Формула средней кубической величины применяется при расчете с величинами кубических функций и исчисляется по формуле:

средняя кубическая

(простая)

Х - индивидуальное значение.

N – число единиц изучаемой совокупности.

(взвешенная)

fi – частота ряда распределения или удельный вес в совокупности.

37.

Средняя геометрическая величина дает возможность сохранять в неизменном виде не сумму, а произведение индивидуальных значений данной величины. Ее можно определить по следующей формуле:

Средние геометрические величины наиболее часто используются при анализе темпов роста экономических показателей.

Геометрическая простая

Для расчетов средней геометрической простой используется формула: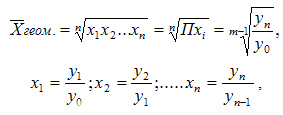

http://www.grandars.ru/images/1/review/id/349/2657168c52.jpg

где:

— цепной коэффициент роста
— число этих коэффициентов роста
П — знак произведения
— количество уровней ряда
— значение начального уровня ряда
— значение конечного уровня ряда

Геометрическая взвешенная
Для определения средней геометрической взвешенной применяется формула:

1 2 3 4