Часть окружности, ограниченная двумя точками, называется дугой окружности.
Дуга называется полуокружностью, если отрезок, соединяющий ее концы, является диаметром окружности.
Кругом называется часть плоскости, ограниченная окружностью.
Круговым сектором называется часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.
1. Все радиусы одной окружности имеют одну и ту же длину.
2. Диаметр окружности в два раза больше ее радиуса.
3. Центр окружности являются серединой любого диаметра.
4. Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.
5. Дуги окружности, заключенные между параллельными хордами, равны.
6. Точка касания двух окружностей лежит на линии их центров.
7. Если через точку Р, лежащую вне окружности, проведены две секущие, пересекающие ее соответственно в точках A, B и C, D, то PA·PB=PC·PD.
8. Если через точку, лежащую вне окружности, проведены две секущие, то угол между ними измеряется полуразностью дуг, заключенных внутри угла.
1. Если расстояние от центра окружности до прямой меньше радиуса окружности, то прямая и окружность имеют две общие точки (прямая – секущая).
2. Если расстояние от центра окружности до прямой равно радиусу окружности, то прямая и окружность имеют только одну общую точку (прямая – касательная).
3. Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общих точек.
|
1. Если расстояние между центрами двух окружностей равно сумме их радиусов, то эти окружности касаются.
2. Через любые три точки, не лежащие на одной прямой, можно провести окружность, и притом только одну.
Формулы:
1. d = 2r.
2.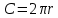 , С , С 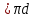 – длина окружности. – длина окружности.
3. l 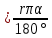 – длина дуги окружности, соответствующая центральному углу α. – длина дуги окружности, соответствующая центральному углу α.
4. Площадь круга равна S =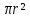 . .
5. Площадь кругового сектора равна
S = 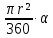 . .
|
29
|
Касательная
к окружности
|
Прямая, имеющая с окружностью только одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности.
|
1. Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.
2. Отрезки касательных к окружности, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
3. Если через точку А проведены касательная AB (В точка – касания) и секущая, которая пересекает окружность в точках C и D, то AC·AD= AB2.
|
1. Если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна к этому радиусу, то она является касательной.
2. Если расстояние от центра окружности до прямой равно радиусу окружности, то прямая и окружность имеют только одну общую точку, т. е. касаются.
|
30
|
Центральный угол
|
Угол с вершиной в центре окружности называется ее центральным углом.
|
1. Если дуга окружности меньше полуокружности или является полуокружностью, то ее градусная мера считается равной градусной мере центрального угла.
2. Если же дуга больше полуокружности, то ее градусная мера считается равной 360° – градусная мера центрального угла.
|
|
31
|
Вписанный угол
|
Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным углом.
|
1. Вписанный угол измеряется половиной дуги, на которую он опирается.
2. Вписанные углы, опирающиеся на одну и ту же дугу равны.
3. Вписанный угол, опирающийся на полуокружность – прямой.
4. Вписанный угол либо равен половине соответствующего ему центрального угла, либо дополняет половину этого угла до 180°.
|
|
32
|
Вписанная
окружность
|
Если все стороны многоугольника касаются окружности, то окружность называется вписанной в многоугольник, а многоугольник – описанным около этой окружности.
|
1. В любой треугольник можно вписать только одну окружность. Центр этой окружности – точка пересечения биссектрис углов треугольника. Радиус вписанной в треугольник окружности – перпендикуляр, опущенный из центра окружности к любой стороне треугольника.
2. r = 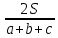 - радиус вписанной в треугольник окружности, - радиус вписанной в треугольник окружности,
a, b, c – стороны треугольника, S – площадь треугольника.
3. Не во всякий четырехугольник можно вписать окружность. В любом описанном четырехугольнике суммы противоположных сторон равны.
4. Площадь описанного многоугольника равна половине произведения его периметра на радиус вписанной окружности.
|
1. Если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность.
2. Если в параллелограмм можно вписать окружность, то этот параллелограмм – ромб.
|
33
|
Описанная
окружность
|
Если все вершины многоугольника лежат на окружности, то окружность называется описанной около многоугольника, а многоугольник – вписанным в эту окружность.
|
1. Около любого треугольника можно описать только одну окружность. Центр этой окружности – точка пересечения серединных перпендикуляров к сторонам треугольника. Радиус – расстояние от центра окружности до любой из вершин треугольника.
2. R = 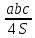 - радиус описанной около треугольника окружности, a, b, c – стороны треугольника, S – площадь треугольника. - радиус описанной около треугольника окружности, a, b, c – стороны треугольника, S – площадь треугольника.
2. Около четырехугольника не всегда можно описать окружность. В любом вписанном четырехугольнике сумма противоположных углов равна 180°.
|
1. Если сумма противоположных углов четырехугольника равна 180°, то около него можно описать окружность.
2. Если около параллелограмма можно описать окружность, то этот параллелограмм – прямоугольник.
|
34
|
Правильные
многоугольники
|
Правильным многоугольником называется выпуклый многоугольник, у которого все углы равны и все стороны равны.
|
1. Около любого правильного многоугольника можно описать окружность и притом только одну.
2. В любой правильный многоугольник можно вписать окружность и притом только одну.
3. Окружность, вписанная в правильный многоугольник, касается сторон многоугольника в их серединах.
4. Центр окружности, описанной около правильного многоугольника, совпадает с центром окружности, вписанной в тот же многоугольник. Эта точка называется центром правильного многоугольника.
n
|
треугольник
|
квадрат
|
шестиугольник
|
α
|
60°
|
90°
|
120°
|
an
|
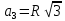
|
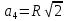
|
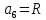
|
R
|
R = 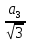
|
R = 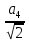
|
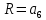
|
r
|
r = 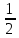 R R
|
r = 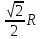
|
r = 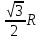
|
|
Формулы:
1. 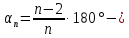 вычисление угла многоугольника. вычисление угла многоугольника.
2.S = 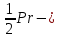 площадь. площадь.
3. аn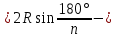 сторона многоугольника. сторона многоугольника.
4. 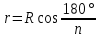
5. R = 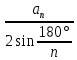
6. R = 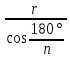 , где n – число сторон, , где n – число сторон,
R– радиус описанной окружности,
r– радиус вписанной окружности,
Р – периметр
|
35
|
Расстояние
|
Расстоянием между двумя точками называется длина отрезка, соединяющего эти точки.
|
|
|
Расстояниемот точки до прямой называется длина перпендикуляра, проведенного из этой точки к данной прямой.
|
Перпендикуляр, проведенный из точки к прямой, меньше любой наклонной, проведенной из той же точки к этой прямой.
|
|
Расстояние от произвольной точки одной из параллельных прямых до другой прямой называется расстоянием между этими прямыми.
|
Все точки каждой из двух параллельных прямых равноудалены от другой прямой.
|
|
 Скачать 76.72 Kb.
Скачать 76.72 Kb.