моделирование. Неиронные сети Искусственная неиронная сеть (ann)

• Название: Неиронные сети Искусственная неиронная сеть (ann)
• Анкор: моделирование
• Дата: 22.05.2023
• Размер: 424.56 Kb.
• Имя файла: MO_laba_2.docx
• Тип: Документы; #1150285

Нейронные сети

Искусственная нейронная сеть (ANN) представляющая собой вычислительную нелинейную модель, которая выполняет такие задачи, как классификация, прогнозирование, принятие решений, визуализация и другие, просто рассматривая примеры.

Искусственная нейронная сеть состоит из искусственных нейронов или элементов обработки и организована в три взаимосвязанных слоя: вход, скрытый, который может содержать более одного уровня, и выход.

Искусственная нейронная сеть делится на четыре вида: ➢Пиковая нейронная сеть

➢Свёрточная нейронная сеть (CNN)
➢Рекуррентная нейронная сеть (RNN)

➢Гибридная нейронная сетевая архитектура (HNNA)

➢Нейронная сеть может быть представлена направленным графом с взвешенными связями, в котором искусственные нейроны являются вершинами, а синаптические связи - дугами.

➢Среди областей применения нейронных сетей - автоматизация процессов распознавания образов, прогнозирование, адаптивное управление, создание экспертных систем, организация ассоциативной памяти, обработка аналоговых и цифровых сигналов, синтез и идентификация электронных цепей и систем.

➢С помощью нейронных сетей можно, предсказывать объемы продаж изделий, показатели биржевого рынка, выполнять распознавание сигналов, конструировать самообучающиеся системы.

➢Модели нейронных сетей могут быть программного и аппаратного исполнения.
➢Если говорить простым языком, слоистая нейронная сеть представляет собой совокупность нейронов, которые составляют слои.

➢В каждом слое нейроны между собой никак не связаны, но связаны с нейронами предыдущего и следующего слоев.
➢Информация поступает с первого на второй слой, со второго - на третий и т.д.

Применение нейронных сетей

Классификация (обучение с учителем). распознавание текста, распознавание речи, идентификация личности.

Прогнозировани найти наилучшее приближение функции, заданной конечным набором входных значений (обучающих примеров). Например, нейронные сети позволяют решать задачу восстановления пропущенных значений.

Кластеризация (обучение без учителя). задача сжатия информации путем уменьшения размерности данных. Задачи кластеризации решаются, например, самоорганизующимися картами Кохонена.

Медицинская диагностика. В ходе наблюдения за различными показателями состояния пациентов накоплена база данных. Риск наступления осложнений может соответствовать сложной нелинейной комбинации наблюдаемых переменных, которая обнаруживается с помощью нейросетевого моделирования.

Прогнозирование показателей деятельности фирмы (объемы продаж). На основе ретроспективной информации о деятельности организации возможно определение объемов продаж на будущие периоды. Предоставление кредита. Используя базу данных о клиентах банка, применяя нейронные сети, можно установить группу клиентов, которые относятся к группе потенциальных "неплательщиков".

Примеры задач, решаемых с помощью нейронных сетей

➢Прогнозирование на фондовом рынке. Зная цены акций за последнюю неделю и сегодняшнее значение индекса FTSE, спрогнозировать завтрашнюю цену акций.

➢Предоставление кредита. Требуется определить, высок ли риск предоставления кредита частному лицу, обратившемуся с такой просьбой. В результате разговора с ним известен его доход, предыдущая кредитная история и т.д.

Особенности применения нейронных сетей для решения задач

сеть можно применять в ситуации, когда имеется определенная известная информация, и необходимо из нее получить некоторую пока неизвестную информацию; необходимо знать (или хотя бы иметь серьезные подозрения), что между известными входными значениями и неизвестными выходами имеется связь.

➢ Искусственная нейронная сеть – компьютерная программа, моделирующая способ Обработки мозгом конкретной задачи

Нейрон получает сигналы (импульсы) от аксонов других нейронов через дендриты и передает сигналы, сгенерированные телом клетки, вдоль своего аксона, который в конце разветвляется на волокна. На окончаниях этих волокон находятся специальные образования - синапсы, которые влияют на величину импульсов.

Искусственный нейрон — узел искусственной нейронной сети, являющийся упрощённой моделью естественного нейрона.
Математически, искусственный нейрон обычно представляют как некоторую нелинейную функцию от единственного аргумента — линейной комбинации всех входных сигналов. Данную функцию называют функцией активации или функцией срабатывания, передаточной функцией. Полученный результат посылается на единственный выход. Такие искусственные нейроны объединяют в сети — соединяют выходы одних нейронов с входами других.

Элементы нейронных сетей

Главная функция искусственного нейрона - формировать выходной сигнал в зависимости от сигналов, поступающих на его входы.

Нейрон характеризуется текущим состоянием и обладает группой синапсов - однонаправленных входных связей, соединенных с выходами других нейронов.
Нейрон имеет аксон - выходную связь данного нейрона, с которой сигнал (возбуждения или торможения) поступает на синапсы следующих нейронов. Каждый синапс характеризуется величиной синаптической связи

Текущее состояние нейрона определяется как взвешенная сумма его входов: Выход нейрона есть функция его состояния: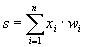



Активационная функция

Активационная функция- это
нелинейная функция, вычисляющая выходной сигнал формального нейрона.

Часто используемые активационные функции: ➢Жесткая пороговая функция.
➢Линейный порог.
➢Сигмоидальная функция.

Выбор активационной функции определяется спецификой поставленной задачи либо ограничениями, накладываемыми некоторыми алгоритмами обучения.
Нелинейный преобразователь - это элемент искусственного нейрона, преобразующий текущее состояние нейрона (выходной сигнал адаптивного сумматора) в выходной сигнал нейрона по некоторому нелинейному закону ( активационной функции ).

Точка ветвления (выход) - это элемент формального нейрона, посылающий его выходной сигнал по нескольким адресам и имеющий один вход и несколько выходов.
На вход точки ветвления обычно подается выходной сигнал нелинейного преобразователя, который затем посылается на входы других нейронов.

Алгоритм

1. 
   получить входные значения;
   
2. 
   вычислить значение активации (взвешенная сумма входа – пороговое значение);
   
3. 
   преобразовать значение активации с помощью функции активации.
   

Пре/пост процессирование

Функция активации для каждого элемента сети обычно выбирается таким образом, чтобы ее входной аргумент мог принимать произвольные значения, а выходные лежали бы в строго ограниченном диапазоне значений ("сплющивание").

При этом, возникает эффект насыщения, когда элемент оказывается чувствительным лишь к входным значениям, лежащим в некоторой ограниченной области.

На рисунке выходное значение всегда будет лежать в интервале (0,1), а область чувствительности для входов чуть шире интервала (-1,+1). Данная функция является гладкой, а ее производная легко вычисляется - это обстоятельство весьма существенно для работы алгоритма обучения сети.

Масштабирование

Числовые значения должны быть приведены в масштаб, подходящий для сети. Обычно исходные данные масштабируются по линейной шкале*.

Номинальные переменные

➢Номинальная переменная числовая переменная (Пол = {Муж, Жен}
Муж = 0, Жен = 1)

➢Кодирование 1-из-N: (Животное = {Собака, Овца, Кошка} Собака = {1,0,0}, Овца = {0,1,0}, Кошка = {0,0,1})

Архитектура нейронных сетей

Нейронные сети могут быть синхронные и асинхронные.
В синхронных нейронных сетях в каждый момент времени свое состояние меняет лишь один нейрон.
В асинхронных - состояние меняется сразу у целой группы нейронов, как правило, у всего слоя.
Можно выделить две базовые архитектуры - слоистые и полносвязные сети . Ключевым в слоистых сетях является понятие слоя.
Слой - один или несколько нейронов, на входы которых подается один и тот же общий сигнал.
Слоистые нейронные сети - нейронные сети, в которых нейроны разбиты на отдельные группы так, что обработка информации осуществляется послойно.

В слоистых сетях нейроны 𝑖-го слоя получают входные сигналы, преобразуют их и через точки ветвления передают нейронам (𝑖 +1) слоя. И так до 𝑘-го слоя, который выдает выходные сигналы для интерпретатора и пользователя. Число нейронов в каждом слое не связано с количеством нейронов в других слоях, может быть произвольным.

В рамках одного слоя данные обрабатываются параллельно, а в масштабах всей сети обработка ведется последовательно - от слоя к слою.

Слоистые сети, в свою очередь, могут быть однослойными и многослойными.
Однослойная сеть - сеть, состоящая из одного слоя. Многослойная сеть - сеть, имеющая несколько слоев.

В многослойной сети первый слой называется входным, последующие - внутренними или скрытыми, последний слой - выходным. Таким образом, промежуточные слои - это все слои в многослойной нейронной сети, кроме входного и выходного.

Входной слой сети реализует связь с входными данными, выходной - с выходными.
Таким образом, нейроны могут быть входными, выходными и скрытыми. Входной слой организован из входных нейронов (input neuron), которые получают данные и распространяют их на входы нейронов скрытого слоя сети. Скрытый нейрон (hidden neuron) - это нейрон, находящийся в скрытом слое нейронной сети.

Выходные нейроны (output neuron), из которых организован выходной слой сети, выдает результаты работы нейронной сети.
В полносвязных сетях каждый нейрон передает свой выходной сигнал остальным нейронам, включая самого себя. Выходными сигналами сети могут быть все или некоторые выходные сигналы нейронов после нескольких тактов функционирования сети. Все входные сигналы подаются всем нейронам

Обучение нейронных сетей

Перед использованием нейронной сети ее необходимо обучить.
Процесс обучения нейронной сети заключается в подстройке ее внутренних параметров под конкретную задачу.
Алгоритм работы нейронной сети является итеративным, его шаги называют эпохами или циклами.
Эпоха - одна итерация в процессе обучения, включающая предъявление всех примеров из обучающего множества и, возможно, проверку качества обучения на контрольном множестве.
Процесс обучения осуществляется на обучающей выборке.
Обучающая выборка включает входные значения и соответствующие им выходные значения набора данных. В ходе обучения нейронная сеть находит некие зависимости выходных полей от входных.

Таким образом, ставится вопрос - какие входные поля (признаки) необходимо использовать.
Первоначально выбор осуществляется эвристически, далее количество входов может быть изменено.

При увеличении количества признаков количество наблюдений возрастает нелинейно, эта проблема носит название "проклятие размерности".

При недостаточном количестве данных рекомендуется использовать линейную модель.
Аналитик должен определить количество слоев в сети и количество нейронов в каждом слое.

Веса и смещения автоматически настраиваются таким образом, чтобы минимизировать разность между желаемым и полученным на выходе сигналами, которая называется ошибка обучения. Ошибка обучения для построенной нейронной сети вычисляется путем сравнения выходных и целевых (желаемых) значений. Из полученных разностей формируется функция ошибок.

Функция ошибок - это целевая функция, требующая минимизации в процессе управляемого обучения нейронной сети.
С помощью функции ошибок можно оценить качество работы нейронной сети во время обучения.

От качества обучения нейронной сети зависит ее способность решать поставленные перед ней задач

Процесс обучения нейронной сети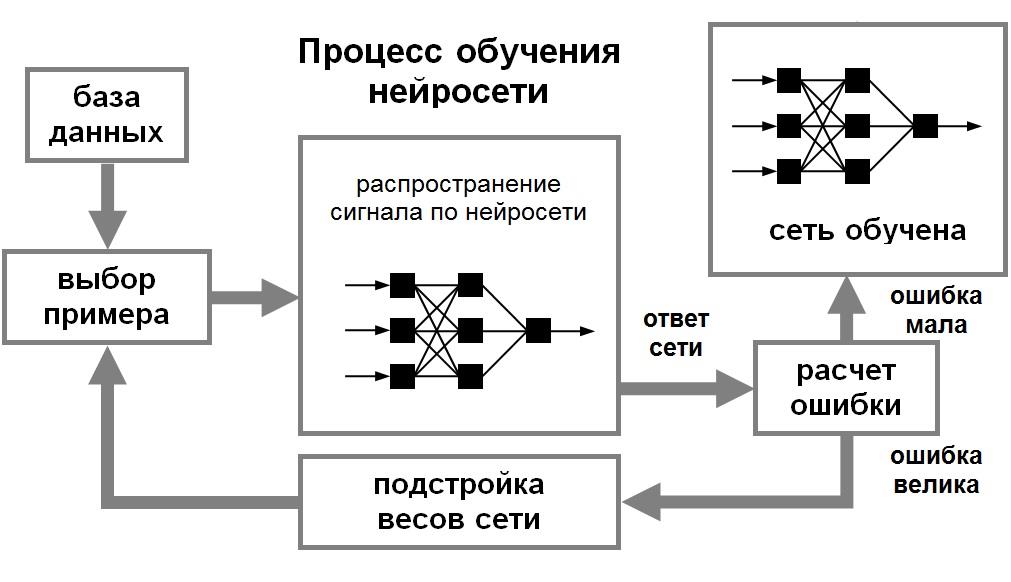



Алгоритмы обучения нейронной сети

Обучение с учителем

1. 
   Подготавливается набор обучающих данных. Эти данные представляют собой примеры входных данных и соответствующих им выходов. Сеть учится устанавливать связь между первыми и вторыми;
   
2. 
   Нейронная сеть обучается с помощью того или иного алгоритма управляемого обучения, при котором имеющиеся данные используются для корректировки весов и пороговых значений сети таким образом, чтобы минимизировать ошибку прогноза на обучающем множестве.
   

Обучение без учителя

1. 
   Обучающие данные содержат только значения входных переменных.
   
2. 
   Сеть учится распознавать внутреннюю структуру данных.
   

Сбор данных для нейронной сети

Требования к обучающему множеству:

➢Множество не должно содержать всплесков – элементы, свойства которых отличаются от ожидаемых значений;

➢Элементы множества должны быть репрезентативны;
➢Обучающая выборка должна быть в несколько раз больше общего количества

весовых связей в сети;
➢Частные требования.
Выводы:

➢Выбирайте такие переменные, которые, как Вы предполагаете, влияют на результат.

➢С числовыми и номинальными переменными можно работать непосредственно. Переменные других типов следует преобразовать в указанные типы или объявить незначащими.

➢Чем больше в задаче переменных, тем больше нужно иметь наблюдений.
➢ В случае необходимости можно работать с наблюдениями, содержащими пропущенные значения. Если возможно, удалите выбросы. Если данных достаточное количество, уберите из рассмотрения наблюдения с пропущенными значениями.

Подготовка данных для обучения

➢Количество наблюдений в наборе данных. Следует учитывать тот фактор, что чем больше размерность данных, тем больше времени потребуется для обучения сети. ➢Работа с выбросами. Следует определить наличие выбросов и оценить необходимость их присутствия в выборке.

➢Обучающая выборка должна быть представительной (репрезентативной). ➢Обучающая выборка не должна содержать противоречий, так как нейронная сеть однозначно сопоставляет выходные значения входным.
➢Нейронная сеть работает только с числовыми входными данными, поэтому важным этапом при подготовке данных является преобразование и кодирование данных. При использовании на вход нейронной сети следует подавать значения из того диапазона, на котором она обучалась. Например, если при обучении нейронной сети на один из ее входов подавались значения от 0 до 10, то при ее применении на вход следует подавать значения из этого же диапазона или близлежащие.

Существует понятие нормализации данных.
Целью нормализации значений является преобразование данных к виду, который наиболее подходит для обработки, т.е. данные, поступающие на вход, должны иметь числовой тип, а их значения должны быть распределены в определенном диапазоне.
Нормализатор может приводить дискретные данные к набору уникальных индексов либо преобразовывать значения, лежащие в произвольном диапазоне, в конкретный диапазон, например, [0..1].
Нормализация выполняется путем деления каждой компоненты входного вектора на длину вектора, что превращает входной вектор в единичный.

Выбор структуры нейронной сети

Выбор структуры нейронной сети обусловливается спецификой и сложностью решаемой задачи. В большинстве случаев выбор структуры нейронной сети определяется на основе объединения опыта и интуиции разработчика.

Однако существуют основополагающие принципы, которыми следует руководствоваться при разработке новой конфигурации :
➢возможности сети возрастают с увеличением числа ячеек сети, плотности связей между ними и числом выделенных слоев;

➢введение обратных связей наряду с увеличением возможностей сети поднимает вопрос о динамической устойчивости сети;
➢сложность алгоритмов функционирования сети (в том числе, например, введение нескольких типов синапсов - возбуждающих, тормозящих и др.) также способствует усилению мощи НС.

Переобучение нейронной сети

При обучении нейронных сетей часто возникает серьезная трудность, называемая проблемой переобучения
Переобучение - излишне точное соответствие нейронной сети конкретному набору обучающих примеров, при котором сеть теряет способность к обобщению.

возникает в случае слишком долгого обучения, недостаточного числа обучающих примеров или переусложненной структуры нейронной сети.

связано с тем, что выбор обучающего множества является случайным. С первых шагов обучения происходит уменьшение ошибки. На последующих шагах с целью уменьшения ошибки параметры подстраиваются под особенности обучающего множества. Однако при этом происходит "подстройка" не под общие закономерности ряда, а под особенности его части - обучающего подмножества. При этом точность прогноза уменьшается.

Переобучение нейронной сети

Один из вариантов борьбы с переобучением сети - деление обучающей выборки на два множества (обучающее и тестовое).
На первом шаге ошибки прогноза для обучающего и тестового множества одинаковы. На последующих шагах значения обеих ошибок уменьшаются, однако с семидесятого шага ошибка на тестовом множестве начинает возрастать, т.е. начинается процесс переобучения сети.

Сложности применения НС

➢Для построения модели объекта на основе НС требуется выполнение многоцикловой настройки внутренних элементов и связей между ними;

➢ Проблемы, возникающие при подготовке обучающей выборки, связанные с трудностями нахождения достаточного количества обучающих примеров;

➢Обучение сети в ряде случаев приводит к тупиковым ситуациям; ➢Продолжительные временные затраты на выполнение процедуры обучения зачастую не позволяют применять ИНС в системах реального времени;
➢ Поведение обученной ИНС не всегда может быть однозначно предсказуемо, что увеличивает риск применения ИНС для управления дорогостоящими техническими объектами;
➢Обучить и эксплуатировать нейронную сеть для решения многих задач, как правило, может и не специалист, но надежно интерпретировать результаты, а также численно оценивать значимость получаемых прогнозов способны специалисты, имеющие навыки в моделировании нейронных сетей.

Модели нейронных сетей

Персептрон

Большое количество моделей персептрона рассмотрено в основополагающей работе Розенблатта.
Простейшая модель нейронной сети - однослойный персептрон.
Однослойный персептрон (персептрон Розенблатта) - однослойная нейронная сеть, все нейроны которой имеют жесткую пороговую функцию активации. Однослойный персептрон имеет простой алгоритм обучения и способен решать лишь самые простые задачи.

Классический пример такой нейронной сети - однослойный трехнейронный персептрон.

Перцептрон Розенблатта

Модель Мак-Каллока – Питтса была реализована Фрэнком Розенблаттом: в 1958 г. в виде компьютерной модели (перцептрона), в 1960 г. в виде электронного устройства, распознававшего рукописные изображения некоторых букв и цифр – первого в мире нейрокомпьютера Марк-1.

Однослойный персептрон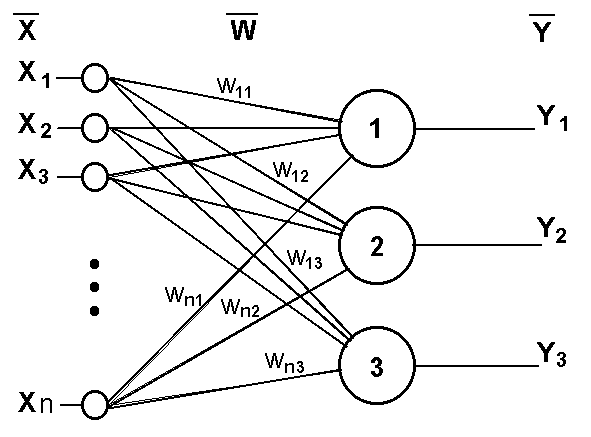




Сеть, изображенная на рисунке, имеет 𝑛 входов, на которые поступают сигналы, идущие по синапсам на 3 нейрона. Эти три нейрона образуют единственный слой данной сети и выдают три выходных сигнала.

Алгоритм обучения персептрона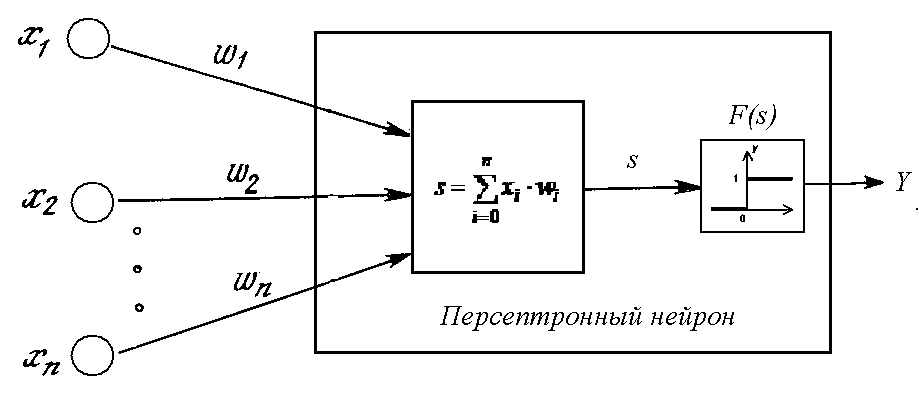



Многослойный персептрон

Многослойный персептрон (MLP) - нейронная сеть прямого распространения сигнала в которой входной сигнал преобразуется в выходной, проходя последовательно через несколько слоев.

В этой модели персептрона должен быть хотя бы один скрытый слой. Присутствие нескольких таких слоев оправдано лишь в случае использования нелинейных функций активации.

Двухслойный перцептрон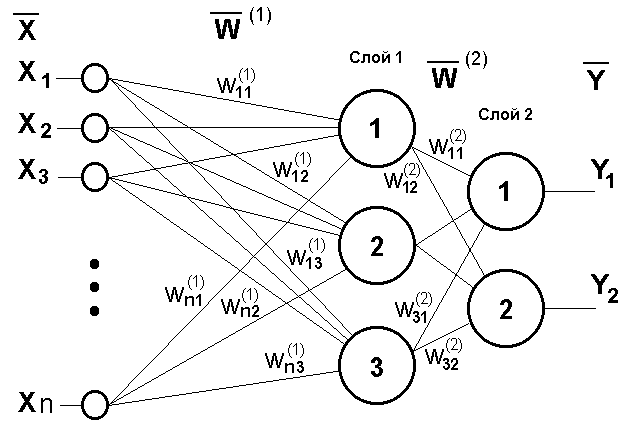



Сеть, изображенная на рисунке, имеет n входов. На них поступают сигналы, идущие далее по синапсам на 3 нейрона, которые образуют первый слой. Выходные сигналы первого слоя передаются двум нейронам второго слоя. Последние, в свою очередь, выдают два выходных сигнала.

Многослойных персептрон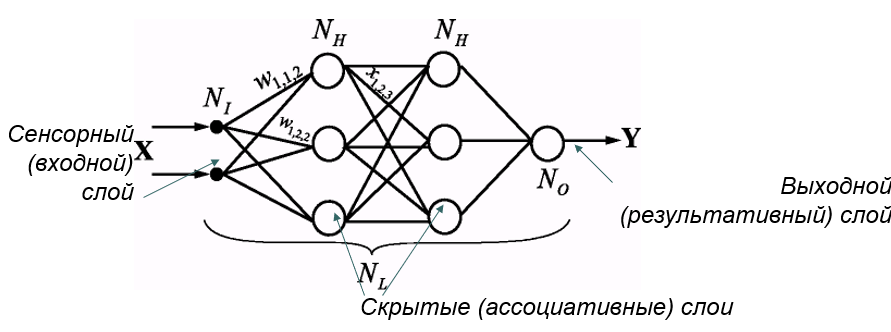



Обучение многослойного персептрона

➢Принцип связи между нейронами - "каждый с каждым".

➢Количество нейронов в слоях может быть произвольным.

➢Обычно во всех скрытых слоях одинаковое количество нейронов.

➢Входной слой только распределяет сигналы.

Целью обучения является поиск таких значений весов и порогов сети, которые бы минимизировали ошибку прогноза, выдаваемого сетью.
Функции ошибок:

➢сумма квадратов ошибок; ➢среднеквадратическая ошибка.

Многослойные нейронные сети



Глубокая нейронная сеть – сеть с большим числом скрытых слоев

Линейная сеть

Линейная модель сети – это сеть без промежуточных слоев, которая в выходном слое содержит только линейные элементы.

Во время работы сеть фактически умножает вектор входов на матрицу весов, а затем к полученному вектору прибавляет вектор смещения (вектор пороговых значений).

Может оказаться так, что задачу, считавшуюся очень сложной, можно успешно не только нейронной сетью, но и простым линейным методом. Если же в задаче не так много обучающих данных, то, вероятно, просто нет оснований использовать более сложные модели.

Структура линейной сети

Линейные сети по своей структуре аналогичны персептрону и отличаются лишь функцией активации.
Выход линейной сети может принимать любое значение, в то время как выход персептрона ограничен значениями 0 или 1.

На рис. * показан линейный нейрон с двумя входами. Он имеет структуру, сходную со структурой персептрона. Единственное отличие состоит в том, что используется линейная функция активации. Весовая матрица W в этом случае имеет только одну строку, и выход сети определяется выражением:

𝒂 = 𝒇(𝒏) = 𝒇(𝑾𝒑+𝒃) =𝑾𝒑+𝒃 = 𝒘_𝟏𝟏𝒑_𝟏 + 𝒘_𝟏𝟐𝒑_𝟐 +𝒃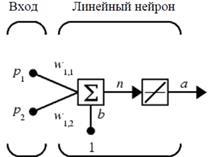



Подобно персептрону, линейная сеть задает в пространстве входов разделяющую линию, на которой функция активации 𝑛 равна 0 (рис. **).
Векторы входа, расположенные выше этой линии, соответствуют положительным значениям выхода, а расположенные ниже – отрицательным. Это означает, что линейная сеть может быть применена для решения задач классификации.

Однако такая классификация может быть выполнена только для класса линейно отделимых объектов. Таким образом, линейные сети имеют то же самое ограничение, что и персептрон.

Рис.**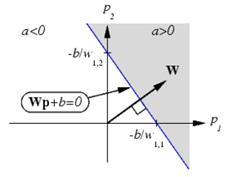



Классификация нейронных сетей

Одна из возможных классификаций нейронных сетей - по направленности связей. Нейронные сети бывают с обратными связями и без обратных связей.
Сети без обратных связей
Сети с обратным распространением ошибки. Сети этой группы характеризуются фиксированной структурой, итерационным обучением, корректировкой весов по ошибкам

Преимуществами сетей без обратных связей является простота их реализации и гарантированное получение ответа после прохождения данных по слоям. Недостатком считается минимизация размеров сети - нейроны многократно участвуют в обработке данных. Меньший объем сети облегчает процесс обучения.

Сети с обратными связями

➢Сети Хопфилда (задачи ассоциативной памяти).
➢Сети Кохонена (задачи кластерного анализа).
Преимуществами сетей с обратными связями является сложность обучения, вызванная большим числом нейронов для алгоритмов одного и того же уровня сложности.
Недостатки этого вида сетей - требуются специальные условия, гарантирующие сходимость вычислений.

Классификация нейронных сетей

Другая классификация нейронных сетей: сети прямого распространения и рекуррентные сети.
Сети прямого распространения
➢Персептроны.

➢Сеть Back Propagation.
➢Сеть встречного распространения.
➢Карта Кохонена.
Рекуррентные сети. Характерная особенность таких сетей - наличие блоков динамической задержки и обратных связей, что позволяет им обрабатывать динамические модели.
➢Сеть Хопфилда.
➢Сеть Элмана - сеть, состоящая из двух слоев, в которой скрытый слой охвачен динамической обратной связью, что позволяет учесть предысторию наблюдаемых процессов и накопить информацию для выработки правильной стратегии управления. Эти сети применяются в системах управления движущимися объектами.

Нейронные сети могут обучаться с учителем или без него.
При обучении с учителем для каждого обучающего входного примера требуется знание правильного ответа или функции оценки качества ответа. Такое обучение называют управляемым. Нейронной сети предъявляются значения входных и выходных сигналов, а она по определенному алгоритму подстраивает веса синаптических связей. В процессе обучения производится корректировка весов сети по результатам сравнения фактических выходных значений с входными, известными заранее.
При обучении без учителя раскрывается внутренняя структура данных или корреляции между образцами в наборе данных. Выходы нейронной сети формируются самостоятельно, а веса изменяются по алгоритму, учитывающему только входные и производные от них сигналы. Это обучение называют также неуправляемым. В результате такого обучения объекты или примеры распределяются по категориям, сами категории и их количество могут быть заранее не известны. Обучение с подкреплением
Нет правильных ответов, но в процессе обучения сеть получает сигналы от внешней среды, которая при взаимодействии дает обратную связь . То есть, это обучение через опыт — так же, как учатся люди в течение жизни.

Самоорганизующиеся карты

Разведочный анализ данных. Сеть Кохонена способна распознавать кластеры в данных, а также устанавливать близость классов. Таким образом, пользователь может улучшить свое понимание структуры данных, чтобы затем уточнить нейросетевую модель.

Обнаружение новых явлений. Сеть Кохонена распознает кластеры в обучающих данных и относит все данные к тем или иным кластерам. Если после этого сеть встретится с набором данных, непохожим ни на один из известных образцов, то она не сможет классифицировать такой набор и тем самым выявит его новизну.

Сеть Кохонена

Сеть рассчитана на неуправляемое обучение.

Возможности применения:

➢распознавать кластеры в данных; ➢устанавливать близость классов; ➢выявлять новизну данных.

В процессе обучения и функционирования сеть

выполняет 3 процесса:

➢ конкуренция;
➢ объединение; ➢подстройка весов.

Процесс обучения сети можно разделить на две фазы:

➢фаза грубой подстройки; ➢фаза точной подстройки.

После того, как сеть обучена распознаванию структуры данных, ее можно использовать как средство визуализации при анализе данных, при котором можно определить разбивается ли карта на отдельные кластеры.
Далее, как только кластеры выявлены, нейроны топологической карты помечаются содержательными по смыслу метками (в некоторых случаях помечены могут

Карты Кохонена (как и географические карты) можно отображать:
➢в двухмерном виде, тогда карта раскрашивается в соответствии с уровнем выхода нейрона;
➢в трехмерном виде.

В результате работы алгоритма получаем такие карты: ➢карта входов нейронов ;
➢карта выходов нейронов ;


Карта входов нейронов.
Веса нейронов подстраиваются под значения входных переменных и отображают их внутреннюю структуру. Для каждого входа рисуется своя карта, раскрашенная в соответствии со значением конкретного веса нейрона.
При анализе данных используют несколько карт входов.
На одной из карт выделяют область определенного цвета - это означает, что соответствующие входные примеры имеют приблизительно одинаковое значение соответствующего входа. Цветовое распределение нейронов из этой области анализируется на других картах для определения схожих или отличительных характеристик.

Карта выходов нейронов.
На карту выходов нейронов проецируется взаимное расположение исследуемых входных данных. Нейроны с одинаковыми значениями выходов образуют кластеры - замкнутые области на карте, которые включают нейроны с одинаковыми значениями выходов.

Специальные карты.
Это карта кластеров, матрица расстояний, матрица плотности попадания и другие карты, которые характеризуют кластеры, полученные в результате обучения сети Кохонена.

Пример работы Сети Кохонена

Имеется множество данных, в которых содержатся атрибуты «Возраст» и «Доход», которые были предварительно нормализованы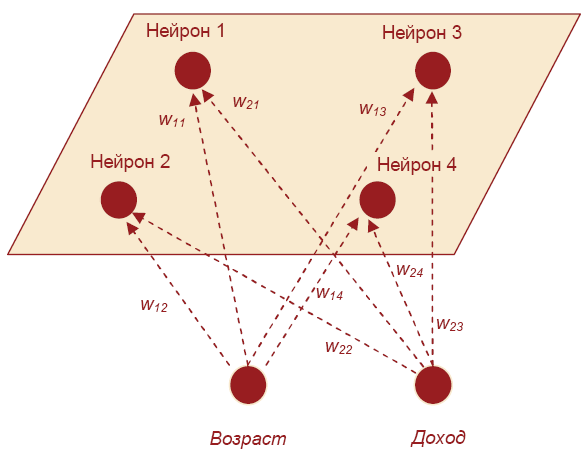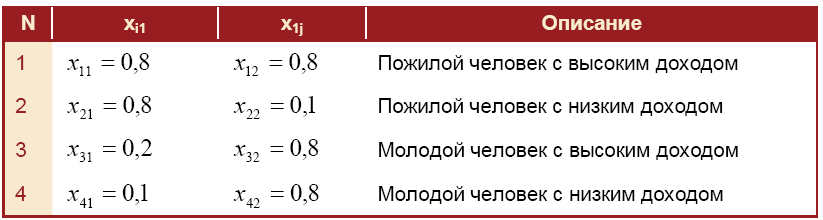