Глава 8 Неоднородные вычисления. Неоднородные вычисления Содержание Глава Неоднородные вычисления Основы неоднородных вычислений
 Скачать 0.62 Mb. Скачать 0.62 Mb.
|
|
Как это работает... Наш декоратор @guvectorize обрабатывает аргументы массивов, получая четыре аргумента для определения значения сигнатуры gufunc: Первые три аргумента определяют значения типов данных для управления и массивы целых значений: void(int64[:,:], int64[:,:], int64[:,:]). Последний аргумент @guvectorize описывает как манипулировать установленными размерностями матриц: (m,n),(n,p)->(m,p). Затем определяется операция матричного умножения, где A и B выступают в роли входных матриц, а C это выходная матрица: A(m,n)* B(n,p) = C(m,p), где m, n и p являются размерностями матриц. Произведение матриц выполняется посредством трёх циклов for совместно со значениями индексов матриц: for i in range(m): for j in range(p): C[i, j] = 0 for k in range(n): C[i, j] += A[i, k] * B[k, j] Для построения входных матриц с размерностью 10 × 10 применяется функция NumPy randint: dim = 10 A = np.random.randint(dim,size=(dim, dim)) B = np.random.randint(dim,size=(dim, dim)) Наконец, для этих матриц в качестве аргументов вызывается наша функция matmul и выводится на печать получаемая в результате матрица C: C = matmul(A, B) print("RESULT MATRIX C = A*B") print(":\n%s" % C) Для выполнения этого примера наберите следующее: (base) C:\> python matMulNumba.py Приводятся результаты заданных двух матриц и полученную в результате их умножения матрицу: INPUT MATRIX A : [[8 7 1 3 1 0 4 9 2 2] [3 6 2 7 7 9 8 4 4 9] [8 9 9 9 1 1 1 1 8 0] [0 5 0 7 1 3 2 0 7 3] [4 2 6 4 1 2 9 1 0 5] [3 0 6 5 1 0 4 3 7 4] [0 9 7 2 1 4 3 3 7 3] [1 7 2 7 1 8 0 3 4 1] [5 1 5 0 7 7 2 3 0 9] [4 6 3 6 0 3 3 4 1 2]] INPUT MATRIX B : [[2 1 4 6 6 4 9 9 5 2] [8 6 7 6 5 9 2 1 0 9] [4 1 2 4 8 2 9 5 1 4] [9 9 1 5 0 5 1 1 7 1] [8 7 8 3 9 1 4 3 1 5] [7 2 5 8 3 5 8 5 6 2] [5 3 1 4 3 7 2 9 9 5] [8 7 9 3 4 1 7 8 0 4] [3 0 4 2 3 8 8 8 6 2] [8 6 7 1 8 3 0 8 8 9]] RESULT MATRIX C = A*B : [[225 172 201 161 170 172 189 230 127 169] [400 277 289 251 278 276 240 324 295 273] [257 171 177 217 208 254 265 224 176 174] [187 130 116 117 94 175 105 128 152 114] [199 133 117 143 168 156 143 214 188 157] [180 118 124 113 152 149 175 213 167 122] [238 142 186 165 188 215 202 200 139 192] [237 158 162 176 122 185 169 140 137 130] [249 160 220 159 249 125 201 241 169 191] [209 152 142 154 131 160 147 161 132 137]] Также ознакомьтесь... Написание алгоритма для операции снижения ранга при помощи PyCUDA может быть достаточно сложным. Для этой цели Numba предоставляет декоратор @reduce для преобразования простых двоичных операций в понижающие ядра (reduction kernels). Операции снижения ранга сводят набор значений к отдельному значению. Типичным примером понижающей операции является вычисление суммы всех элементов массива. в качестве примера рассмотрим следующий массив элементов: 1, 2, 3, 4, 5, 6, 7, 8. Последовательный алгоритм работает так, как это показано на следующей схеме, то есть добавляя элементы данного массива один за другим: Рисунок 8-7 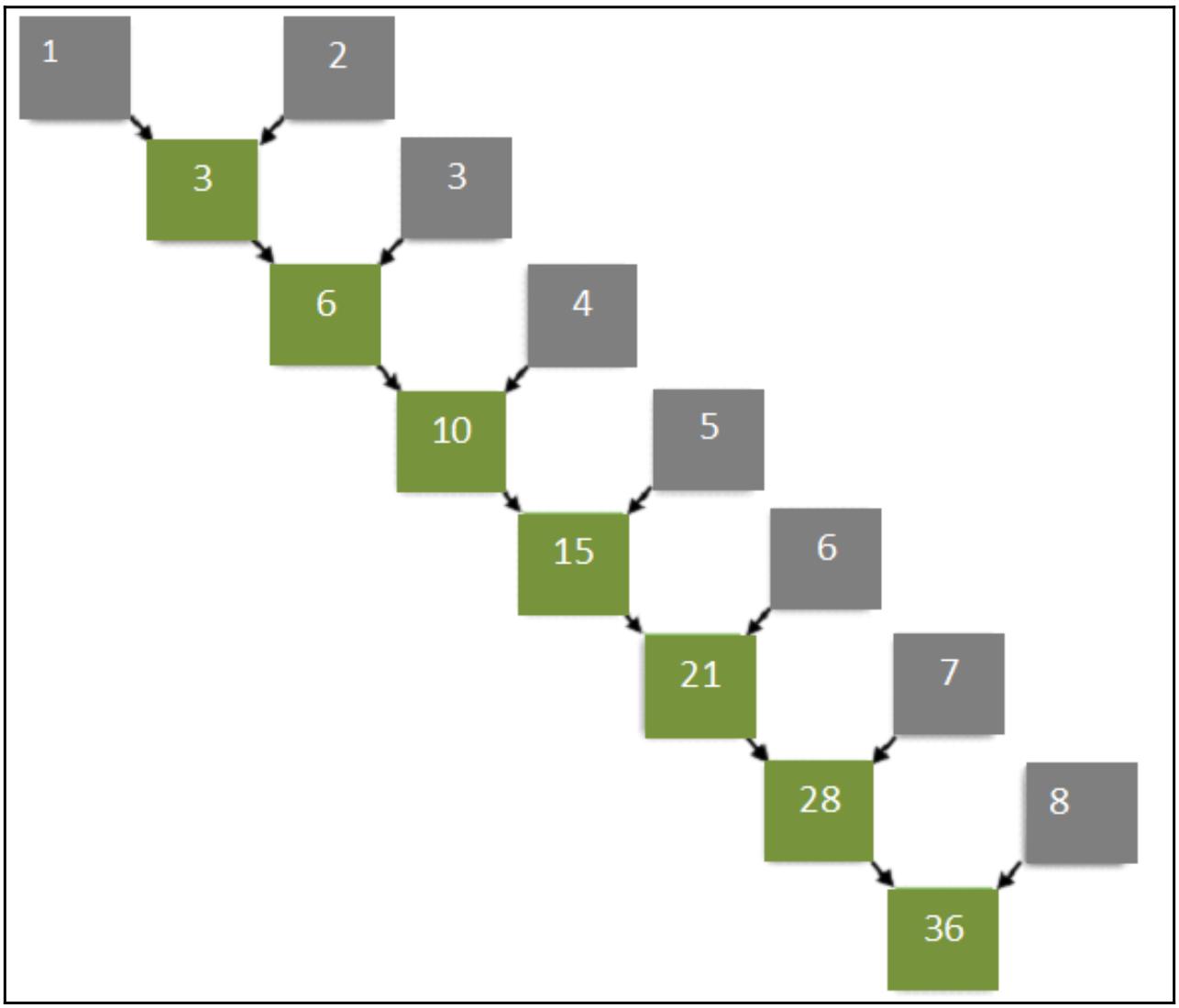 Последовательное суммирование Параллельный же алгоритм работает по следующей схеме: Рисунок 8-8 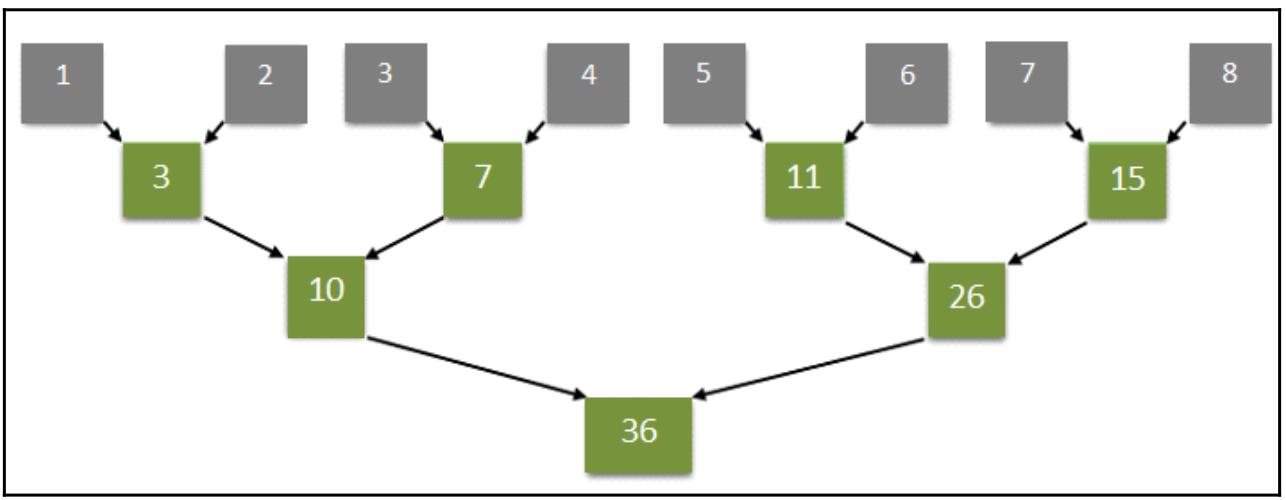 Параллельное суммирование Становится ясно, что последний имеет определённое преимущество в сокращении времени исполнения. С помощью Numba и установленного декоратора @reduce мы способны написать некий алгоритм в несколько строк кода для значения параллельного суммирования некого массива целых в диапазоне от 1 до 10 000: import numpy from numba import cuda @cuda.reduce def sum_reduce(a, b): return a + b A = (numpy.arange(10000, dtype=numpy.int64)) + 1 print(A) got = sum_reduce(A) print(got) Наш предыдущий пример может быть выполнен после набора такой команды: (base) C:\> python reduceNumba.py Будет представлен такой результат: vector to reduce = [ 1 2 3 ... 9998 9999 10000] result = 50005000 |
