Глава 8 Неоднородные вычисления. Неоднородные вычисления Содержание Глава Неоднородные вычисления Основы неоднородных вычислений

• Название: Неоднородные вычисления Содержание Глава Неоднородные вычисления Основы неоднородных вычислений
• Дата: 27.12.2022
• Размер: 0.62 Mb.
• Имя файла: Глава 8 Неоднородные вычисления.docx
• Тип: Глава; #866699
• страница: 2 из 8

Наши блоки разрабатываются с тем, чтобы гарантировать масштабирование. На практике, когда у вас имеется архитектура с двумя процессорами и другая с четырьмя, тогда приложение GPU может выполняться в обеих архитектурах с различными временами и уровнями параллельности.

Для выполнения некой неоднородной программы в соответствии с рассматриваемой моделью программирования PyCUDA, оно строится следующим образом:

1. 
   Выделяем память в своём хосте.
   
2. 
   Пересылаем данные из имеющейся памяти хоста в память необходимого устройства.
   
3. 
   Запускаем своё устройство через вызов имеющихся функций ядра.
   
4. 
   Пересылаем результаты из памяти устройства в память его хоста.
   
5. 
   Высвобождаем память, выделенную данному устройству.
   

Следующая схема отображает обсуждаемый поток выполнения программы в соответствии с моделью программирования PyCUDA:

 

Рисунок 8-3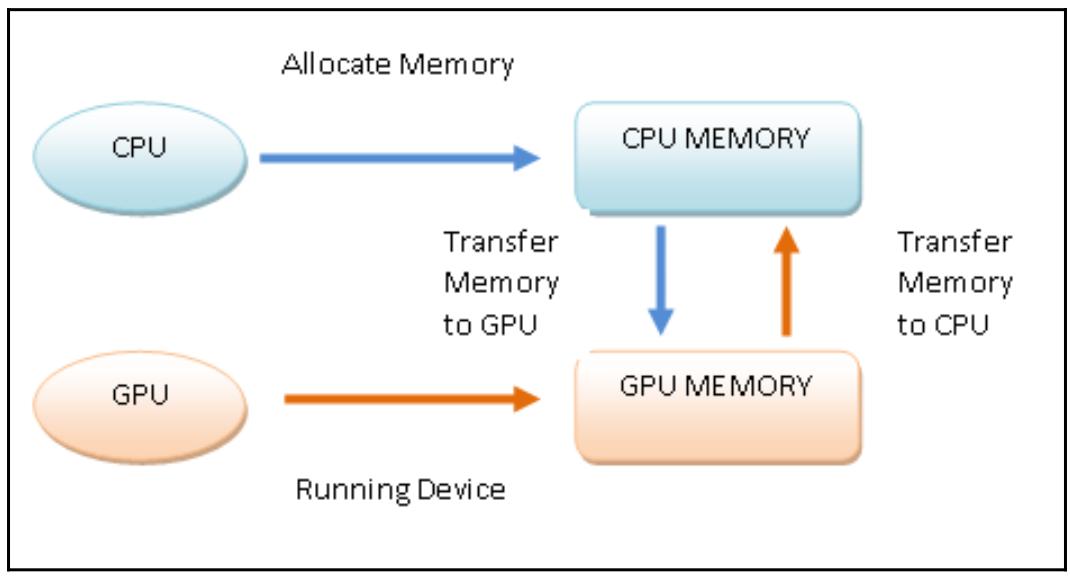


Модель программирования PyCUDA
В своём следующем примере мы пройдёмся по конкретному примеру данной методологии программирования чтобы следовать порядку построения приложений PyCUDA.

Как это сделать...

Для демонстрации модели программирования PyCUDA мы рассмотрим задачу дублирования всех элементов в матрице 5 х 5:

1. 
   Мы импортируем те библиотеки, которые необходимы для задач, которые мы собрались решать:
   
2. 
   
   
3. 
   import PyCUDA.driver as CUDA
   
4. 
   import PyCUDA.autoinit
   
5. 
   from PyCUDA.compiler import SourceModule
   
6. 
   import numpy
   

7. 
   И импортируемая нами библиотека numpy позволяет нам строить ввод для нашей задачи, а именно, матрицу 5 x 5, значения которой выбираются случайным образом:
   
8. 
   
   
9. 
   a = numpy.random.randn(5,5)
   
10. 
    a = a.astype(numpy.float32)
    

11. 
    Наша построенная подобным образом матрица должна быть скопирована из основной памяти своего хоста в память выполняющего вычисления устройства. Для этого мы выделяем некое пространство памяти (a_gpu) в этом устройстве, которое требуется для хранения матрицы a. С этой целью мы применяем функцию mem_alloc, которая должна в качестве своего предмета должна выделить необходимое пространство памяти. В частности, общее число байт матрицы a выражается значением параметра a.nbytes следующим образом:
    
12. 
    
    
13. 
    a_gpu = cuda.mem_alloc(a.nbytes)
    

14. 
    После этого мы сможем переслать свою матрицу из главного хоста в ту область памяти, которая создана целенаправленно в вычислительном устройстве при помощи функции memcpy_htod:
    
15. 
    
    
16. 
    cuda.memcpy_htod(a_gpu, a)
    

17. 
    Внутри вычислительного устройства будет работать функция ядра doubleMatrix. Её целью будет умножение всех элементов матрицы на 2. Как вы можете видеть, синтаксис этой функции doubleMatrix аналогичен С, в то время как наш оператор SourceModule является реальной директивой для компилятора nVidia (компилятор nvcc), создающий некий модуль, который в данном случае состоит всего лишь из нашей функции doubleMatrix:
    
18. 
    
    
19. 
    mod = SourceModule("""
    
20. 
    __global__ void doubles_matrix(float *a){
    
21. 
    int idx = threadIdx.x + threadIdx.y*4;
    
22. 
    a[idx] *= 2;}
    
23. 
    """)
    

24. 
    При помощи параметра func мы указываем свою функцию doubleMatrix, которая содержится в нашем модуле mod:
    
25. 
    
    
26. 
    func = mod.get_function("doubles_matrix")
    

27. 
    Наконец, мы запускаем свою функцию ядра. Для успешного выполнения некой функции ядра в имеющемся устройстве, пользователь CUDA должен задать необходимый ввод для этого ядра и значение размера своего блока потока. В нашем следующем случае имеется входная матрица a_gpu, которая ранее была скопирована в это устройство, в то время как размерность нашего блока потока равна (5,5,1):
    
28. 
    
    
29. 
    func(a_gpu, block=(5,5,1))
    

30. 
    Следовательно, мы выделяем область памяти по размеру эквивалентную своей входной матрице a:
    
31. 
    
    
32. 
    a_doubled = numpy.empty_like(a)
    

33. 
    Далее мы копируем содержимое области памяти выделенное устройству - то есть свою матрицу a_gpu - в ранее определённую область памяти, a_doubled:
    
34. 
    
    
35. 
    cuda.memcpy_dtoh(a_doubled, a_gpu)
    

36. 
    Наконец, мы выводим на печать содержимое своей входной матрицы и полученную в результате матрицу чтобы убедиться в качестве своей реализации:
    
37. 
    
    
38. 
    print ("ORIGINAL MATRIX")
    
39. 
    print (a)
    
40. 
    print ("DOUBLED MATRIX AFTER PyCUDA EXECUTION")
    
41. 
    print (a_doubled)
    

Как это работает...

Давайте начнём с просмотра импортируемых нами библиотек:
import PyCUDA.driver as CUDA

import PyCUDA.autoinit

from PyCUDA.compiler import SourceModule



В частности, наш импорт autoinit автоматически определяет какой именно GPU в нашей системе доступен для работы, в то время как SourceModule является директивой для того компилятора nVidia (nvcc), который позволит нам указать неободимые объекты, подлежащие компиляции и выгрузке в соответствующее устройство.

Далее при помощи библиотеки numpy мы строим свою входную матрицу 5 х 5:
import numpy

a = numpy.random.randn(5,5)



В данном случае все элементы нашей матрицы преобразуются в режиме одинарной точности (так как та графическая карта, на которой исполняется данный пример, поддерживает только одинарную точность):
a = a.astype(numpy.float32)



Далее мы копируем свой массив из основного хоста в имеющееся устройство при помощи следующих двух операций:
a_gpu = CUDA.mem_alloc(a.nbytes)

CUDA.memcpy_htod(a_gpu, a)



Обратите внимание, что и само устройство и его хост могут никогда не взаимодействовать в процессе самого исполнения некой функции ядра. По этой причине для параллельного исполнения такой функции ядра в этом устройстве все те данные, которые относятся к самой функции ядра должны также присутствовать в памяти вычислительного устройства.

Также следует обратить внимание что наша матрица a_gpu линеаризована, то есть имеет одно измерение, а следовательно должна обрабатываться именно так.

Более того, все эти действия не требуют вызовов ядра. Это означает, что они напрямую выполняются самим хостом.

Логический элемент SourceModule делает возможным определение нашей функции ядра doubleMatrix. __global__, который выступает в роли директивы nvcc, указывает на то, что данная функция doubleMatrix будет обрабатываться в вычислительном устройстве:
mod = SourceModule("""

__global__ void doubleMatrix(float *a)



Давайте рассмотрим тело нашего ядра. Значение параметра idx является индексом матрицы, которая посредством threadIdx.x и threadIdx.y указывает координаты потока:
int idx = threadIdx.x + threadIdx.y*4;

a[idx] *= 2;



Далее mod.get_function("doubleMatrix") возвращает некий идентификатор для значения параметра func:
func = mod.get_function("doubleMatrix ")



Для выполнения своего ядра нам требуется настроить значение контекста исполнения. Это означает настройку соответствующей трёхмерной структуры имеющихся потоков, которые относятся к создаваемому блоку решётки при помощи значения параметра блока внутри самого вызова func:
func(a_gpu, block = (5, 5, 1))



block = (5, 5, 1) сообщает нам что мы вызываем некую функцию ядра с соответствующей лианеризованной входной матрицей a_gpu и единственным блоком с размером 5 (то есть с 5 потоками) в направлении x-, 5 потоками по направлению y- и 1 потоком в направлении z-, что создаёт в сумме 16 потоков. Обратите внимание, что каждый из потоков исполняет один и тот же код ядра (в сумме 25 потоков).

После вычисления в имеющемся устройстве GPU мы пользуемся неким массивом для сохранения полученных результатов:
a_doubled = numpy.empty_like(a)

CUDA.memcpy_dtoh(a_doubled, a_gpu)



Для выполнения нашего примера в приглашении своей Командной строки наберите следующее:
C:\> python heterogenousPycuda.py



Получаемый вывод должен выглядеть как- то так:
ORIGINAL MATRIX

[[-0.59975582 1.93627465 0.65337795 0.13205571 -0.46468592]

[ 0.01441949 1.40946579 0.5343408 -0.46614054 -0.31727529]

[-0.06868593 1.21149373 -0.6035406 -1.29117763 0.47762445]

[ 0.36176383 -1.443097 1.21592784 -1.04906416 -1.18935871]

[-0.06960868 -1.44647694 -1.22041082 1.17092752 0.3686313 ]]
DOUBLED MATRIX AFTER PyCUDA EXECUTION

[[-1.19951165 3.8725493 1.3067559 0.26411143 -0.92937183]

[ 0.02883899 2.81893158 1.0686816 -0.93228108 -0.63455057]

[-0.13737187 2.42298746 -1.2070812 -2.58235526 0.95524889]

[ 0.72352767 -2.886194 2.43185568 -2.09812832 -2.37871742]

[-0.13921736 -2.89295388 -2.44082164 2.34185504 0.73726263 ]]



Также ознакомьтесь...

Основным ключевым свойством CUDA, которое делает эту модель программирования по большей части отличающейся от прочих моделей программирования (обычно применяемых в ЦПУ), состоит в том, что для достижения эффективности она требует задействовать тысячи потоков. Это делает возможным в обычных структурах GPU, которые применяют потоки с малым весом, а также допускают создание и изменение контекста выполнения очень быстрым и действенным образом.

Обратите внимание, что планирование потоков напрямую связано с имеющейся архитектурой GPU и присущему ей параллелизму. На практике некий блок потоков назначается отдельному SM. Здесь все потоки далее делятся на группы посредством имеющегося обёртывающего планировщика (warp scheduler). Для достижения полного преимущества внутренне присущего параллелизма существующих SM и потоков одна и та же обёртка обязана выполнять одну и ту же инструкцию. Когда такое условие не выполняется, мы говорим о расхождении потоков (threads divergence).

Дополнительно

• 
  Полное руководство по программированию PyCUDA доступно на следующем сайте
  
• 
  Для установки PyCUDA в Windows 10, взгляните на следующую ссылку
  

Реализация управления памятью с применением PyCUDA

Программы PyCUDA обязаны соблюдать предписанные установленной структурой и внутренней организацией SM правила, которые налагают ограничения на производительность потоков. На практике знание и правильное применение различных видов предоставляемых GPU памяти имеют основополагающее значение для достижения максимальной эффективности. В таких GPU, в которых включено использование CUDA, существует четыре следующих вида памяти:

• 
  Регистры: Каждому потоку назначается некий регистр памяти, к которому имеет доступ только назначенный поток, даже если окружающие его потоки относятся к тому же самому блоку.
  
• 
  Разделяемая память: Каждый блок обладает своей собственной памятью, совместно используемой между относящимися к нему потоками. Даже эта память чрезвычайно быстрая.
  
• 
  Постоянная память: Все потоки в некой решётке обладают доступом к хранимым в памяти константам, однако они доступны только на чтение. Эти данные присутствуют в них постоянно на протяжении всего исполнения данного приложения.
  
• 
  Глобальная память: Все существующие в общей решётке потоки, а следовательно и все имеющиеся ядра, имеют доступ к общей памяти. Более того, данные продолжают оставаться там в точности как и в постоянной памяти:
  

 

Рисунок 8-4


Модель памяти GPU

Приготовление

Таким образом, для лучшей производительности некая программа PyCUDA должна максимально использовать все виды имеющейся памяти. В частности она должна максимально применять общую память, сводя к минимуму доступ к глобальной памяти.

Для этого область решаемой задачи обычно подразделяется таким образом, чтобы один блок потоков мог бы выполнять свою обработку в закрытом подмножестве данных. Тем самым, все работающие в одном блоке потоки будут совместно работать в одной и той же области разделяемой памяти, оптимизируя доступ.

Вот основные шаги, которым следует придерживаться всем потокам:

1. 
   Загрузить данные из глобальной памяти в разделяемую память.
   
2. 
   Синхронизовать все потоки определённого блока с тем, чтобы все они могли считывать безопасные позиции из разделяемой памяти, заполняемых прочими потоками.
   
3. 
   Обрабатывать данные в разделяемой памяти. Для гарантии того что эта разделяемая память была обновлена полученными результатами, необходимо выполнение некой новой синхронизации.
   
4. 
   Запись полученных результатов в глобальную память.
   

Для прояснения данного подхода, в своём следующем разделе мы представим некий пример, основывающийся на вычислении произведения двух матриц.

Как это сделать...

Следующий фрагмент кода показывает вычисление произведения двух матриц, M×N, стандартным методом, который основывается на последовательном подходе. Каждый элемент в получаемой в выводе матрице, P, получается после выборки элементов строки из матрицы M и элементов колонки из матрицы N:
void SequentialMatrixMultiplication(float*M,float *N,float *P, int width){

for (int i=0; i< width; ++i)

for(int j=0;j < width; ++j) {

float sum = 0;

for (int k = 0 ; k < width; ++k) {

float a = M[I * width + k];

float b = N[k * width + j];

sum += a * b;

}

P[I * width + j] = sum;

}

}

P[I * width + j] = sum;



В данном случае, когда каждому потоку придаётся необходимая задача вычисления каждого элемента в результирующей матрице, тогда доступ к памяти будет иметь доминирующее значение в общем времени выполнения такого алгоритма.

Что мы можем сделать, так это положиться на некий блок потоков для вычисления одного вывода частичной матрицы за раз. Таким образом, все потоки, которые имеют доступ к одной и той же памяти блока совместно работают для оптимизации доступа, тем самым минимизируя общее время выполнения:

1. 
   Самый первый шаг состоит в загрузке всех необходимых для реализации этого алгоритма модулей:
   
2. 
   
   
3. 
   import numpy as np
   
4. 
   from pycuda import driver, compiler, gpuarray, tools
   

5. 
   Далее инициализируем своё устройство GPU:
   
6. 
   
   
7. 
   import pycuda.autoinit
   

8. 
   Мы реализуем kernel_code_template, который воплощает получение произведения двух матриц, соответственно обозначаемых как a и b, в то время как получаемая в результате матрица обозначается значением параметра c. Обратите внимание, что значение параметра MATRIX_SIZE будет задано на следующем шаге:
   
9. 
   
   
10. 
    kernel_code_template = """
    
11. 
    __global__ void MatrixMulKernel(float *a, float *b, float *c)
    
12. 
    {
    
13. 
    int tx = threadIdx.x;
    
14. 
    int ty = threadIdx.y;
    
15. 
    float Pvalue = 0;
    
16. 
    for (int k = 0; k < %(MATRIX_SIZE)s; ++k) {
    
17. 
    float Aelement = a[ty * %(MATRIX_SIZE)s + k];
    
18. 
    float Belement = b[k * %(MATRIX_SIZE)s + tx];
    
19. 
    Pvalue += Aelement * Belement;
    
20. 
    }
    
21. 
    c[ty * %(MATRIX_SIZE)s + tx] = Pvalue;
    
22. 
    }"""
    

23. 
    наш следующий параметр будет применён для установки значения размерностей наших матриц. В данном случае размером будет 5x5:
    
24. 
    
    
25. 
    MATRIX_SIZE = 5
    

26. 
    Мы задаём две входных матрицы, a_cpu и b_cpu, которые будут содержать случайным образом присваиваемые значения с плавающей точкой:
    
27. 
    
    
28. 
    a_cpu = np.random.randn(MATRIX_SIZE,
    
29. 
    MATRIX_SIZE).astype(np.float32)
    
30. 
    b_cpu = np.random.randn(MATRIX_SIZE,
    
31. 
    MATRIX_SIZE).astype(np.float32)
    

32. 
    После этого вычисляем произведение двух этих матриц, a и b, в своём устройстве хоста:
    
33. 
    
    
34. 
    c_cpu = np.dot(a_cpu, b_cpu)
    

35. 
    Мы выделяем облать памяти вычислительного устройства (GPU), равную размеру входных матриц:
    
36. 
    
    
37. 
    a_gpu = gpuarray.to_gpu(a_cpu)
    
38. 
    b_gpu = gpuarray.to_gpu(b_cpu)
    

39. 
    Выделяем некую область памяти в своём GPU, равную по размеру выходной матрице результата произведения двух своих матриц. В данном случае наша результирующая матрица, c_gpu, имеет размер 5х5:
    
40. 
    
    
41. 
    c_gpu = gpuarray.empty((MATRIX_SIZE, MATRIX_SIZE), np.float32)
    

42. 
    Наш следующий код kernel_code повторно определяет kernel_code_template, но на этот раз с установленным размером matrix_size:
    
43. 
    
    
44. 
    kernel_code = kernel_code_template % {
    
45. 
    'MATRIX_SIZE': MATRIX_SIZE}
    

46. 
    Соответствующая директива SourceModule сообщает nvcc (NVIDIA CUDA Compiler) что ему придётся создать некий модуль - который представляет набор функций - содержащих ранее определённый kernel_code:
    
47. 
    
    
48. 
    mod = compiler.SourceModule(kernel_code)
    

49. 
    Наконец, мы получаем из этого модуля, mod, необходимую функцию MatrixMulKernel, которой мы присваиваем название matrixmul:
    
50. 
    
    
51. 
    matrixmul = mod.get_function("MatrixMulKernel")
    

52. 
    Мы выполняем произведение двух матриц, a_gpu и b_gpu, получая в результате матрицу c_gpu. Значение размера блока потоков определяется как MATRIX_SIZE, MATRIX_SIZE, 1:
    
53. 
    
    
54. 
    matrixmul(
    
55. 
    a_gpu, b_gpu,
    
56. 
    c_gpu,
    
57. 
    block = (MATRIX_SIZE, MATRIX_SIZE, 1))
    

58. 
    Выводим на печать входные матрицы:
    
59. 
    
    
60. 
    print ("-" * 80)
    
61. 
    print ("Matrix A (GPU):")
    
62. 
    print (a_gpu.get())
    
63. 
    print ("-" * 80)
    
64. 
    print ("Matrix B (GPU):")
    
65. 
    print (b_gpu.get())
    
66. 
    print ("-" * 80)
    
67. 
    print ("Matrix C (GPU):")
    
68. 
    print (c_gpu.get())
    

69. 
    Чтобы убедиться в правильности вычисления, выполненного в нашем GPU, мы проводим сравнение полученных результатов двух своих реализаций, одна из которых выполнена в вычислительном устройстве хоста (ЦПУ), а вторая осуществлена во внешнем вычислительном устройстве (GPU). Для этого мы воспользуемся директивой numpy allclose, которая поэлементно сличает два массива на равенство с точностью, равной 1e-05:
    
70. 
    
    
71. 
    np.allclose(c_cpu, c_gpu.get())