Глава 8 Неоднородные вычисления. Неоднородные вычисления Содержание Глава Неоднородные вычисления Основы неоднородных вычислений

• Название: Неоднородные вычисления Содержание Глава Неоднородные вычисления Основы неоднородных вычислений
• Дата: 27.12.2022
• Размер: 0.62 Mb.
• Имя файла: Глава 8 Неоднородные вычисления.docx
• Тип: Глава; #866699
• страница: 4 из 8

Дополнительно

• 
  Документация PyOpenCL доступна здесь.
  
• 
  Одно из наилучших введений в PyOpenCL, даже несмотря на свою дату, можно отыскать по следующей ссылке.
  

Построение приложений при помощи PyOpenCL

Самый первый шаг построения программы для PyOpenCL состоит в написании кода самого приложения хоста. Он выполняется на основном ЦПУ и обладает задачей управления всем возможным исполнением своего ядра в имеющейся карте GPU (то есть в вычислительном устройстве).

Некое ядро (kernel) является базовым элементом исполняемого кода, аналогичного функции C. Он может быть параллельным для данных или параллельным для задач. Однако замковым камнем PyOpenCL выступает сама эксплуатация параллелизма.

Основополагающим понятием является некая программа, которая является коллекцией ядер и прочих функций, аналогичных динамическим библиотекам. Поэтому мы обладаем возможностью группирования инструкций в неком ядре и группировании различных ядер в какую- то программу.

Программы могут вызываться из приложений. Мы имеем очереди исполнения, которые указывают установленный порядок, в котором исполняются ядра. Однако, в некоторых случаях их можно запускать не следуя первоначальному порядку.

Наконец, мы можем перечислить все основополагающие элементы для разработки некого приложения при помощи PyOpenCL:

• 
  Устройство (Device): Указывает на само оборудование, в котором должен выполняться необходимый код ядра. Обратите внимание, что приложение PyOpenCL может выполняться как в плате ЦПУ, так и в плате GPU (также как и PyCUDA), а также во встроенных устройствах, таких как FPGA (Field Programmable Gate Arrays, Программируемые пользователями вентильные матрицы).
  
• 
  Программа (Program): Это группа ядер, которая имеет установленную задачу планирования того какие ядра должны запускаться в вычислительном устройстве.
  
• 
  Ядро (Kernel: Это непосредственно код для выполнения в вычислительном устройстве. Некое ядро представляет собой подобную C функцию, что означает, что она может компилироваться в любом устройстве, поддерживающем драйверы PyOpenCL.
  
• 
  Очередь команд (Command queue): Это порядки ввыполнения ядер вычислительного устройства.
  
• 
  Контекст (Context): представляет собой группу устройств, которая позволяет устройствам принимать ядра и обмениваться данными.
  

Ниже приводится схема, отображающая как такая структура данных может работать в неком приложении хоста:

 

Рисунок 8-6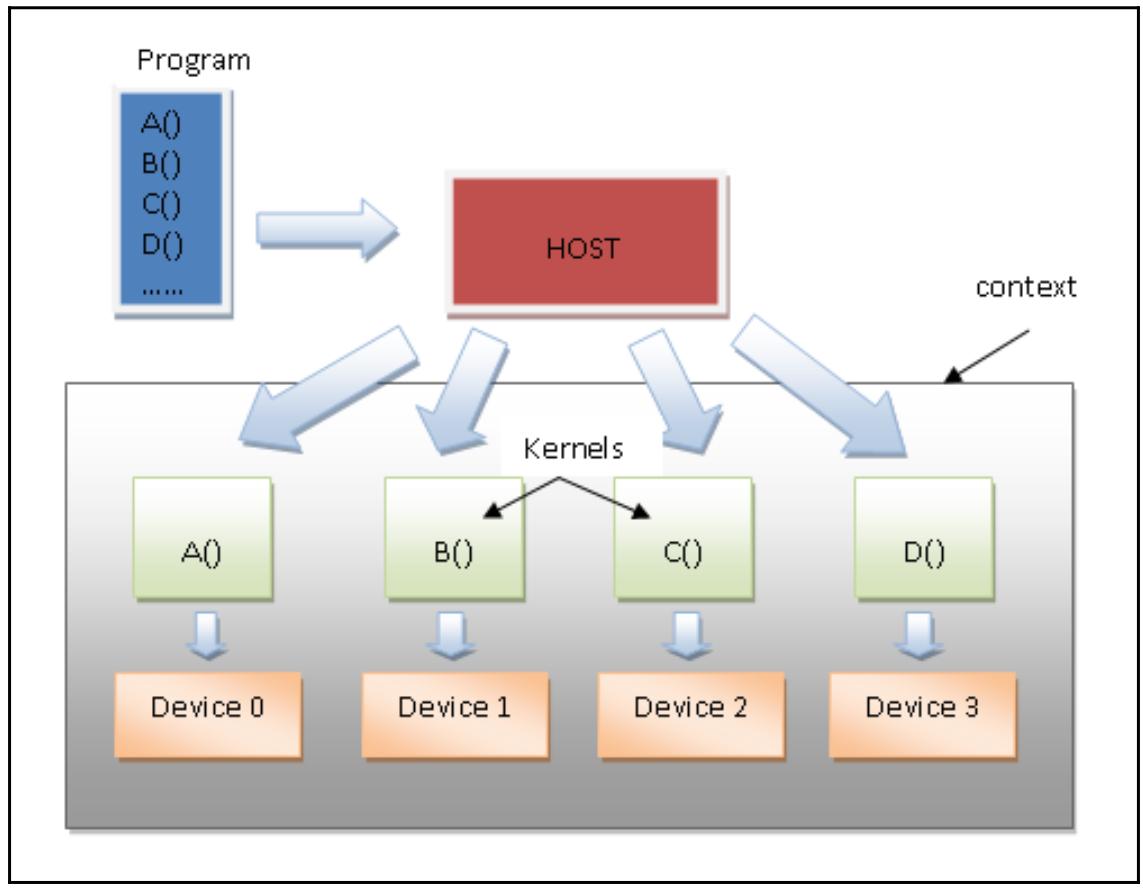


Модель программирования PyOpenCL
И снова мы наблюдаем, что наша программа способна содержать дополнительные функции для исполнения в вычислительном устройстве и что каждое ядро инкапсулирует лишь единственную функцию из имеющейся программы.

Как это сделать...

В своей следующей программе мы покажем все основные шаги построения некого приложения с помощью PyOpenCL: основная задача для выполнения состоит в суммировании двух векторов. Чтобы обладать читаемым выводом, мы рассмотрим два вектора, которые обладают 100 элементами: каждый i-й элемент получаемого вектора будет эквивалентен сумме i-го элемента vector_a с i-м элементом vector_b:

1. 
   Давайте начнём с импорта необходимых библиотек:
   
2. 
   
   
3. 
   import numpy as np
   
4. 
   import pyopencl as cl
   
5. 
   import numpy.linalg as la
   

6. 
   Мы задаём устанавливаемый размер векторов для сложения следующим образом:
   
7. 
   
   
8. 
   vector_dimension = 100
   

9. 
   Здесь определяются наши входные векторы, vector_a и vector_b:
   
10. 
    
    
11. 
    vector_a = np.random.randint(vector_dimension,size=vector_dimension)
    
12. 
    vector_b = np.random.randint(vector_dimension,size=vector_dimension)
    

13. 
    В этой последовательности мы определяем platform device, context и queue:
    
14. 
    
    
15. 
    platform = cl.get_platforms()[1]
    
16. 
    device = platform.get_devices()[0]
    
17. 
    context = cl.Context([device])
    
18. 
    queue = cl.CommandQueue(context)
    

19. 
    Теперь пришло время организации областей в памяти, которые будут содержать наши входные векторы:
    
20. 
    
    
21. 
    mf = cl.mem_flags
    
22. 
    a_g = cl.Buffer(context, mf.READ_ONLY | mf.COPY_HOST_PTR,\ hostbuf=vector_a)
    
23. 
    b_g = cl.Buffer(context, mf.READ_ONLY | mf.COPY_HOST_PTR,\ hostbuf=vector_b)
    

24. 
    Наконец, мы строим необходимое ядро приложение с применением метода Program:
    
25. 
    
    
26. 
    program = cl.Program(context, """
    
27. 
    __kernel void vectorSum(__global const int *a_g, __global const int *b_g, __global int *res_g) {
    
28. 
    int gid = get_global_id(0);
    
29. 
    res_g[gid] = a_g[gid] + b_g[gid];
    
30. 
    }
    
31. 
    """).build()
    

32. 
    Далее мы выделяем необходимую память для своей результирующей матрицы:
    
33. 
    
    
34. 
    res_g = cl.Buffer(context, mf.WRITE_ONLY, vector_a.nbytes)
    

35. 
    После этого мы вызываем необходимую функцию ядра:
    
36. 
    
    
37. 
    program.vectorSum(queue, vector_a.shape, None, a_g, b_g, res_g)
    

38. 
    Необходимое пространство памяти, применяемое для хранения получаемого результата, выделяется в области памяти основного хоста (res_np):
    
39. 
    
    
40. 
    res_np = np.empty_like(vector_a)
    

41. 
    Копируем полученный результат нашего вычисления м только что созданную область памяти:
    
42. 
    
    
43. 
    cl._enqueue_copy(queue, res_np, res_g)
    

44. 
    Наконец, выводим на печать полученные результаты:
    
45. 
    
    
46. 
    print ("PyOPENCL SUM OF TWO VECTORS")
    
47. 
    print ("Platform Selected = %s" %platform.name )
    
48. 
    print ("Device Selected = %s" %device.name)
    
49. 
    print ("VECTOR LENGTH = %s" %vector_dimension)
    
50. 
    print ("INPUT VECTOR A")
    
51. 
    print (vector_a)
    
52. 
    print ("INPUT VECTOR B")
    
53. 
    print (vector_b)
    
54. 
    print ("OUTPUT VECTOR RESULT A + B ")
    
55. 
    print (res_np)
    

56. 
    За этим мы проводим простую проверку чтобы убедиться в том, что значение операции суммирования верное:
    
57. 
    
    
58. 
    assert(la.norm(res_np - (vector_a + vector_b))) < 1e-5
    

Как это работает...

В своих приводимых ниже строках, после надлежащего импорта, мы определяем свои входные векторы:
vector_dimension = 100

vector_a = np.random.randint(vector_dimension, size= vector_dimension)

vector_b = np.random.randint(vector_dimension, size= vector_dimension)



Каждый вектор содержит 100 целых элементов, которые выбираются случайным образом посредством соответствующей функции numpy:
np.random.randint(max integer , size of the vector)



Далее мы выбираем необходимую платформу для получения своих вычислений, воспользовавшись методом get_platform():
platform = cl.get_platforms()[1]



После этого выбираем соответствующее устройство. В нашем случае, platform.get_devices()[0] соответствует графической карте Intel(R) HD Graphics 5500:
device = platform.get_devices()[0]



На своём следующем шаге определяются значения контекста и очереди; PyOpenCL предоставляет соответствующие методы контекста (выбранного устройства) и очереди (выбранного контекста):
context = cl.Context([device])

queue = cl.CommandQueue(context)



Для осуществления вычислений в выбранном устройстве, наш входной вектор копируется в память необходимого устройства:
mf = cl.mem_flags

a_g = cl.Buffer(context, mf.READ_ONLY | mf.COPY_HOST_PTR,\

hostbuf=vector_a)

b_g = cl.Buffer(context, mf.READ_ONLY | mf.COPY_HOST_PTR,\

hostbuf=vector_b)



Далее мы подготавливаем необходимый буфер для получаемого в результате вектора:
res_g = cl.Buffer(context, mf.WRITE_ONLY, vector_a.nbytes)



Вот как задаётся код необходимого ядра:
program = cl.Program(context, """

__kernel void vectorSum(__global const int *a_g, __global const int *b_g, __global int *res_g) {

int gid = get_global_id(0);

res_g[gid] = a_g[gid] + b_g[gid];}

""").build()



Названием нашего ядра является vectorSum, а имеющийся список параметров определяет все типы данных входных аргументов и тип данных на выходе (оба являются векторами целых значений). Внутри самого тела ядра задаётся сумма двух векторов следующей последовательностью шагов:

1. 
   Инициализируется значение индекса вектора: int gid = get_global_id(0).
   
2. 
   Суммируются компоненты полученных векторов: res_g[gid] = a_g[gid] + b_g[gid].
   

В OpenCL (а следовательно и в PyOpenCL), значения буферов присоединяются к контексту (подробнее...), который перемещается в устройство, когда такой буфер применяется в этом устройстве.

Наконец, мы выполняем в своём устройстве vectorSum:
program.vectorSum(queue, vector_a.shape, None, a_g, b_g, res_g)



Для проверки полученного результата мы применяем оператор assert. Он Сверяет полученный результат и выставляет некую ошибку когда результат ложен:
assert(la.norm(res_np - (vector_a + vector_b))) < 1e-5



Получаемый вывод должен выглядеть как- то так:
(base) C:\> python vectorSumPyopencl.py
PyOPENCL SUM OF TWO VECTORS

Platform Selected = Intel(R) OpenCL

Device Selected = Intel(R) HD Graphics 5500

VECTOR LENGTH = 100

INPUT VECTOR A
[45 46 0 97 96 98 83 7 51 21 72 70 59 65 79 92 98 24 56 6 70 64 59 0

96 78 15 21 4 89 14 66 53 20 34 64 48 20 8 53 82 66 19 53 11 17 39 11

89 97 51 53 7 4 92 82 90 78 31 18 72 52 44 17 98 3 36 69 25 87 86 68

85 16 58 4 57 64 97 11 81 36 37 21 51 22 17 6 66 12 80 50 77 94 6 70

21 86 80 69]
INPUT VECTOR B

[25 8 76 57 86 96 58 89 26 31 28 92 67 47 72 64 13 93 96 91 91 36 1 75

2 40 60 49 24 40 23 35 80 60 61 27 82 38 66 81 95 79 96 23 73 19 5 43

2 47 17 88 46 76 64 82 31 73 43 17 35 28 48 89 8 61 23 17 56 7 84 36

95 60 34 9 4 5 74 59 6 89 84 98 25 50 38 2 3 43 64 96 47 79 12 82

72 0 78 5]