реферат математика1. Независимость криволинейных интегралов, теорема Грина!
 Скачать 97.19 Kb. Скачать 97.19 Kb.
|
|
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ «ОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ (ОмГУПС (ОмИИТ))» Кафедра «Высшая математика» РЕФЕРАТ Тема: «Независимость криволинейных интегралов, теорема Грина!» Выполнил студент гр.18А Вигерич Л.Н. Проверил доцент каф «ВМ» Кузнецов В.Ф. Омск 2020 Введение Высшая математика — курс обучения в средних и высших учебных заведениях, включающий высшую алгебру и математический анализ. Высшая математика включает обычно аналитическую геометрию, элементы высшей и линейной алгебры, дифференциальное и интегральное исчисления, дифференциальные уравнения, теорию множеств, теорию вероятностей и элементы математической статистики. Часто используется в экономике и технике. Является обязательным предметом в российских высших учебных заведениях, за исключением специальностей, в которых различные разделы математики разнесены по разным дисциплинам. Содержание Введение………………………………………………..2 Содержание…………………………………………….3 Криволинейный интеграл……………………………4 Теорема Грина…………………………………………5 Независимость криволинейных интегралов………8 Заключение…………………………………………….11 Список Литературы…………………………………..12 Криволинейный интеграл Криволинейный интеграл — интеграл, вычисляемый вдоль какой-либо кривой на плоскости или в пространстве. Утверждения в этой статье приведены для пространства. , но могут быть обобщены на пространство произвольной размерности. Алгоритм вычисления интегральной суммы для функции нескольких переменных f(x, y) по плоской кривой АВ. Ознакомление с понятием криволинейного интеграла первого рода. Представление формулы расчета криволинейного интеграла по пространственной кривой. 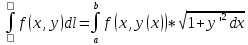 Аппарат криволинейных интегралов значительно расширяет возможности приложений математического анализа к решению задач из механики и физики. Особенно большое значение криволинейные интегралы имеют в теории поля и в теории функций комплексной переменной. Все важные математические понятия получены в связи с исследованием тех или иных практических проблем. Практические задачи также привели к различным криволинейным интегралам. Перечислим некоторые из приложений криволинейных интегралов: вычисление массы материальной линии с переменной линейной плоскостью, работы силового поля, площади плоской фигуры и цилиндрической поверхности и др. Цель работы: исследовать практическое приложение криволинейных интегралов. Теорема Грина. Устанавливает связь между криволинейным интегралом по замкнутому контуру {\displaystyle C}и двойным интегралом по односвязной области {\displaystyle D}, ограниченной этим контуром. Фактически, эта теорема является частным случаем более общей теоремы Стокса. Теорема названа в честь английского математика Джорджа Грина. Формула Грина устанавливает связь между криволинейным интегралом по замкнутому контуру Г на плоскости и двойным интегралом по области, ограниченной данным контуром. ∬R(∂Q/∂x−∂P/∂y)dxdy=∮CP/dx+Q/dy, Замкнутый контур Г мы будем считать кусочно-гладким и без самопересечений. Криволинейный интеграл по замкнутому контуру Г обозначается символом Определение 1. Обход контура Г считается положительным, если при обходе контура Г область D остаётся слева. Г+ — контур Г обходится в положительном направлении, Г — — контур обходится в отрицательном направлении. 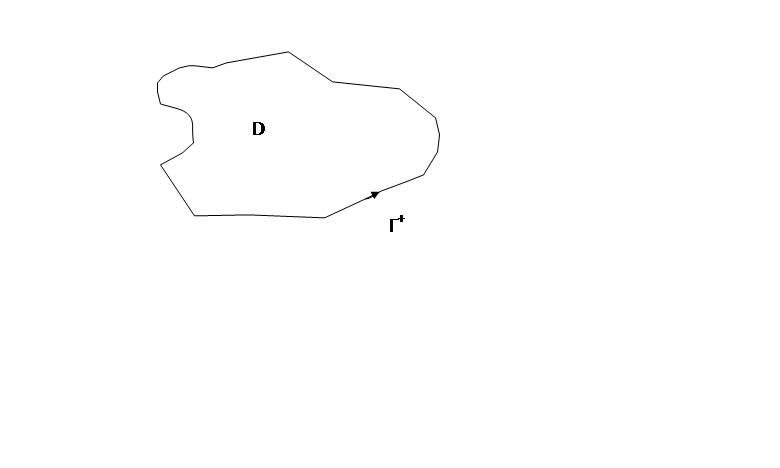 Теорема. Если P(x, y) и Q(x, y) непрерывны вместе со своими частными производными 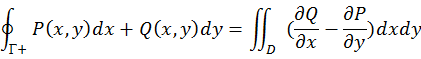 Где Г= Г+ означает, что контур Г обходится в положительном направлении. Доказательство. Доказательство проведем для односвязной области D, т. е. Г= Р 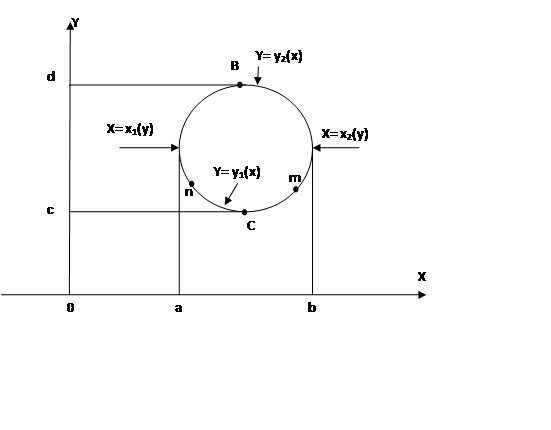 ассмотрим двойной интеграл ассмотрим двойной интеграл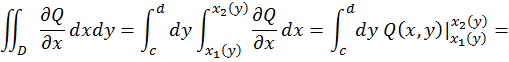 Аналогично доказывается, что: Из равенств (1) и (2) получаем: 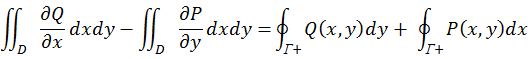 Следовательно, 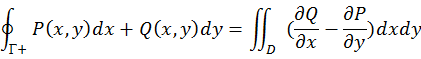 Формула Грина при сделанных предположениях доказана. Замечание 1. Формула Грина остаётся справедливой, если граница Г области D некоторыми прямыми, параллельными оси 0Х или 0Y пересекается более чем в двух точках. Кроме этого формула Грина справедлива и для n-связных областей Независимость криволинейных интегралов Условия независимости криволинейного интеграла от пути интегрирования на плоскости. В этом параграфе выясним условия, при выполнении которых криволинейный интеграл не зависит от пути интегрирования, а зависит от начальной и конечной точек интегрирования. Теорема 1. Для того, чтобы криволинейный интеграл Доказательство: Необходимость. Дано: Пусть в рассматриваемой области D взят произвольный кусочно-гладкий замкнутый контур Г. На контуре Г возьмем произвольные точки B и C. Т  ак как ак как 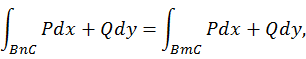 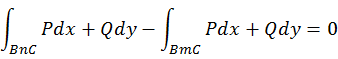 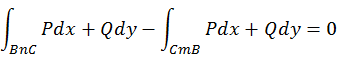 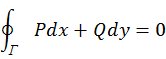 Достаточность. Дано: Криволинейный интеграл Требуется доказать, что интеграл не зависит от пути интегрирования. Рассмотрим криволинейный интеграл по двум кусочно-гладким контурам, соединяющим точки B и С. По условию: 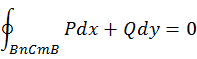 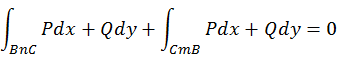 интеграл не зависит от пути интегрирования. Теорема 2. Пусть Доказательство: Достаточность. Дано: 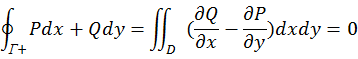 Необходимость. Дано: По теореме 1 криволинейный интеграл Доказательство: Доказательство проведем от противного. Предположим, что Заключение Криволинейный интеграл первого рода и его приложения" были изучены основные теоретические сведения, необходимые для глубокого понимания данной темы, свойства криволинейный интеграл первого рода, а также его приложения: масса кривой с переменной линейной плотностью, площадь цилиндрической поверхности, длина всей кривой, притяжение материальной точки материальной кривой. Также в ней подробно разобраны наглядные примеры на применение криволинейного интеграла первого рода. Список используемой литературы 1. Берман Г.Н. Сборник задач по курсу математического анализа - М.: Наука, 1969. - 440 стр. с илл. 2. Бохан К.А., Егорова И.А., Лащенов К.В. Курс высшей математике. Т. II. - М.: издательство "Просвещение", 1966. https://yandex.ru/search/?text=независимость%20криволинейных%20интегралов%20для%20чего%20используется&lr=66&clid=2069851-321&win=411 |
