Задачи по теме Простые ставки. простые ставки. Простые ставки
 Скачать 27.17 Kb. Скачать 27.17 Kb.
|
|
Тема: «Простые ставки» Задача №1. Доказать следующее утверждение: банковское дисконтирование нельзя осуществить во всех ситуациях, например, по достаточно большой учетной ставке и задолго до срока платежа. Решение Банковское (коммерческое) дисконтирование применяется в ситуации предварительного начисления простого процента, например, при операции по учету векселя, заключающейся в покупке банком векселя у владельца до наступления срока оплаты по цене, меньшей той суммы, которая должна быть выплачена по векселю на дату его погашения. Сумма, которую получает векселедержатель при досрочном учете векселя, называется дисконтированной величиной векселя.  Где  – вложенная сумма; – вложенная сумма; – наращенная сумма; – наращенная сумма; – количество периодов продолжительности финансовой операции; – количество периодов продолжительности финансовой операции; – простая учетная ставка. – простая учетная ставка.Очевидно, величина P должна быть не меньше нуля, поэтому:     Учет векселя по учетной ставке имеет смысл при n<1/d, при n>1/d сумма Р, которую должен получить владелец векселя при его учете, становится отрицательной. Задача №2. Доказать следующее утверждение: математическое дисконтирование выгоднее для векселедержателя, а банковское — для банка. Решение Метод математического дисконтирования применяется, когда необходимо рассчитать сумму денежных средств, которую нужно инвестировать под определенные проценты, чтобы получить требуемую сумму денежных средств, когда необходимо рассчитать проценты, начисленные по процентному финансовому инструменту, а также определить текущую стоимость процентного долгового обязательства. Банковское дисконтирование (банковский учет) применяется при операции по так называемому учету векселей банком или другим финансовым учреждением. Суть операции заключается в следующем. Владелец векселя на сумму F (сумма к погашению) предлагает банку раньше срока оплаты векселя купить его. Покупка векселя у владельца до наступления срока оплаты по цене, меньшей той суммы, которая должна быть выплачена по векселю в конце срока, называется дисконтированием векселя. Сама операция дисконтирования векселя называется учетом векселя. Сумма, которую получает векселедержатель при досрочном учете векселя, называется дисконтированной величиной векселя. Таким образом, векселедержателю досрочно выплачивается обозначенная в векселе сумма за вычетом определенных процентов, удерживаемых банком в свою пользу, называемых дисконтом. Дисконт (Д) представляет собой проценты, начисленные за время (п) со дня дисконтирования до дня погашения векселя на сумму (F), подлежащую уплате в конце срока. Задача №3. Доказать следующее утверждение: при наращении по простой учетной ставке величина начисляемых процентов с каждым годом увеличивается, при наращении капитала по простой процентной ставке капитал ежегодно увеличивается на одну и ту же величину. Решение Схема простых процентов предполагает неизменность базы, с которой происходит начисление. Если исходный инвестируемый капитал равен PV, а требуемая доходность в долях единицы составляет r, то считается, что инвестиция сделана на условиях простого процента, если инвестированный капитал ежегодно увеличивается на величину 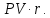 Таким образом, через n лет размер инвестированного капитала будет равен:  Из приведенной формулы видно, что проценты начисляются на одну и ту же величину капитала в течение всего срока. Это выражение называется формулой наращения простыми процентами, а множитель  – множителем наращения или коэффициентом наращения простыми процентами. – множителем наращения или коэффициентом наращения простыми процентами.Из приведенной формулы видно, что приращение капитала составляет величину 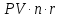 , оно пропорционально сроку ссуды и ставке процента и растет линейно вместе с ростом n. Величину , оно пропорционально сроку ссуды и ставке процента и растет линейно вместе с ростом n. Величину 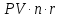 часто называют процентным платежом. часто называют процентным платежом.Необходимо обратить внимание на размерность величин, определяющих размер процентного платежа. Размерности n и r всегда должны быть согласованы. Таким образом, либо n должно измеряться в годах, либо с изменением размерности n (например, не годы, а кварталы) ставка процента должна отражать рост за новую единицу времени (за квартал). Исходя из сказанного наращение по простым процентам в случае, если продолжительность финансовой операции не равна целому числу лет (например, меньше года), определяется по формуле: 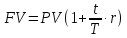 где t – продолжительность финансовой операции в днях; Т - количество дней в году. Наращение по простым процентам применяется при обслуживании депозитных вкладов с ежемесячной выплатой процентов, и вообще в тех случаях, когда проценты не присоединяются к сумме долга, а периодически выплачиваются вкладчику. Простые проценты применяют и при выдаче широко распространенных краткосрочных ссуд, т.е. ссуд, предоставляемых на срок до одного года с однократным начислением процентов. При использовании схемы простых процентов частота начисления не оказывает никакого влияния на суммарную величину процентных денег. Рассмотрим начисление процентов по учетным ставкам, запишем: 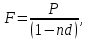 Где  – вложенная сумма; – вложенная сумма; – наращенная сумма; – наращенная сумма; – количество периодов продолжительности финансовой операции; – количество периодов продолжительности финансовой операции; – простая учетная ставка. – простая учетная ставка.Величина начисленных процентов равна:  За первый год капитал возрастет на величину 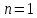  За два года капитал возрастет на величину  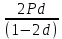 поэтому приращение капитала за год составит:  За три года капитал возрастет на величину 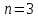  Поэтому приращение капитала за год составит:  За год с номером k капитал возрастет на величину 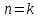  Поэтому приращение капитала с года с номером  составит: составит: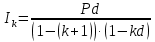 Таким образом,  Так как 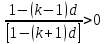 , поэтому начисленные проценты с каждым годом увеличиваются. , поэтому начисленные проценты с каждым годом увеличиваются.Задача №4. Доказать следующее утверждение: простая учетная ставка обеспечивает более быстрый рост капитала, чем такая же по величине процентная ставка. Решение Формула простой учетной ставки:  Где  – вложенная сумма; – вложенная сумма; – наращенная сумма; – наращенная сумма; – количество периодов продолжительности финансовой операции; – количество периодов продолжительности финансовой операции; – простая учетная ставка. – простая учетная ставка.Формула процентной ставки:  Где  – вложенная сумма; – вложенная сумма; – наращенная сумма; – наращенная сумма; – количество периодов продолжительности финансовой операции; – количество периодов продолжительности финансовой операции; – ставка процентов. – ставка процентов.При  получаем: получаем: Таким образом, простая учетная ставка обеспечивает рост капитала быстрее, чем такая же по величине процентная на величину  . .Задача №5. Вы поместили в банк вклад 100 тыс. руб. под простую процентную ставку 6% годовых. Какая сумма будет на счете через 3 года? Какова величина начисленных процентов? Решение при P = 100 тыс. руб., n = 3, r = 0,06 получаем:  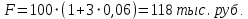 Через три года на счете накопится 118 тыс. рублей. Величина начисленных за три года процентов составит:  Задача№6. На какой срок необходимо поместить денежную сумму под простую процентную ставку 8% годовых, чтобы она увеличилась в 2 раза? Решение Для того, чтобы сумма увеличилась в 2 раза, приравняем множитель наращения к 2:   Сумма, размещенная в банке под 8% годовых, в два раза увеличится через 12,5 лет. Задача №7. Ссуда в сумме 3000 долл. предоставлена 16 января с погашением через 9 месяцев под 25% годовых (год не високосный). Рассчитайте сумму к погашению при различных способах начисления процентов: а) обыкновенный процент с точным числом дней; б) обыкновенный процент с приближенным числом дней; в) точный процент с точным числом дней. Решение а) По формуле  Где  – вложенная сумма; – вложенная сумма; – наращенная сумма; – наращенная сумма; – простая ссудная ставка. – простая ссудная ставка.Используя обыкновенный процент с точным числом дней  , получим: , получим: Сумма к погашению равна 3535,41 долл. б) По формуле  Используя обыкновенный процент с приближенным числом дней, рассчитанным по финансовым таблицам (  ), получим: ), получим:  Сумма к погашению равна 3562,5 долл. в) По формуле  Используя точный процент с точным числом дней  , получим: , получим: Сумма к погашению равна 3528,1 долл. |
