Обыкновенные дроби при реализации системнодеятельностного подхода 13

• Название: Обыкновенные дроби при реализации системнодеятельностного подхода 13
• Дата: 29.03.2023
• Размер: 63.52 Kb.
• Имя файла: Realizatsiia_sistemno_11513801.docx
• Тип: Урок; #1023704

Реализация системно-деятельностного подхода при изучении темы «Обыкновенные дроби»

Содержание

Введение 3

Раздел 1. Теоретические аспекты использования системно-деятельностного подхода при изучении темы обыкновенные дроби 6

1.1. Сущность системно-деятельностного подхода 6

1.2. Современный урок математики с позиции системно-деятельностного подхода 9

Раздел 2. Методические аспекты реализации системно-деятельностного подхода при изучении темы обыкновенные дроби 13

2.1. Комплекс задач по теме «Обыкновенные дроби» при реализации системно-деятельностного подхода 13

2.2. Методы и приемы обучения, позволяющие реализовывать системно-деятельностный подход при изучении обыкновенных дробей 16

Заключение 22

Библиографический список 23

Введение

Сегодня учитель обязан формировать знания, умения учащихся в соответствии с новыми стандартами. В качестве образовательных результатов рассматривается способность и готовность учеников школ самостоятельно осваивать знания, анализировать информацию, извлекать ее из различных источников. Полученные умения и знания формируют компетенции, которые позволяют решать учащимся различные проблемы и задачи, возникающие как в учебной деятельности, так и вне ее, а также позволят ученикам успешно действовать в новой обстановке на качественно высоком уровне. Реализации данных задач в полной мере способствует системно-деятельностный подход в обучении, который выступает методологической основой новых школьных государственных стандартов.

Основная идея данного подхода состоит в том, что овладение учениками новыми знания, умениями, действия, способностями происходит в процессе их самостоятельной учебно-познавательной деятельности. Реализация системно-деятельностного подхода существо изменяет роли и функции участников образовательного процесса. Так учитель переходит на позицию тьютора, фасилитатора, модератора, что позволяют ученику занять равноправную позицию. Они становятся маленькими учеными, делающими свое собственное открытие. Задача учителя состоит в организации деятельности детей по осознанному овладению, закреплению знаниями и умениями. Иными словами научить школьников учиться. Именно это положение служит целью системно-деятельностного подхода.

В настоящее время все более актуальным вопросом является поиск средств реализации системно-деятельностного подхода в образовательном процессе. Анализ психолого-педагогической литературы показывает, что, возникнув на стыке деятельностного и системного подходов, системно-деятельностный подход разработан с общих теоретических положений.

Концептуальные основы данного подхода освящены в трудах А.Г. Асмолова, Л.Г. Петерсон, В.П. Сухов, В.Д. Шадриков и др. Так в работах ученых определены принципы системно-деятельностного подхода, определены основные результаты его реализации в обучении, выраженные в виде универсальных учебных действий. Представлены основная типология уроков в формате системно-деятельностного подхода, намечены основные пути его реализации в тоже время недостаточно представлены конкретные методические основы его реализации в процессе обучения математике.

Поиск эффективных приемов и методов реализации системно-деятельностного подхода в процессе обучения математике, недостаточная разработанность методических аспектов реализации этого подхода в процессе обучения математике обуславливают ее актуальность, проблемой которого является поиск новых подходов к организации учебного процесса математики.

Цель исследования – изучить реализацию системно-деятельностного подхода при изучении темы «Обыкновенные дроби».

Объект исследования: процесс обучения математике учащихся.

Предмет исследования: организация системно-деятельностного подхода при изучении темы «Обыкновенные дроби».

Задачи исследования:

1. Выявить сущность системно-деятельностного подхода.

2. Рассмотреть современный урок математики с позиции системно-деятельностного подхода.

3. Описать комплекс задач по теме «Обыкновенные дроби» при реализации системно-деятельностного подхода.

4. Охарактеризовать методы и приемы обучения, позволяющие реализовывать системно-деятельностный подход при изучении обыкновенных дробей.

Методы исследования: анализ литературы по теме исследования, синтез, обобщение.

Теоретическая значимость исследования заключается в том, что были обобщены и систематизированы сведения о реализации системно-деятельностного подхода на уроках математики.

Практическая значимость исследования заключается в том, что результаты исследования могут быть использованы при организации системно-деятельностного подхода на уроках математики.

Структура работы состоит из введения, двух глав, заключения и списка использованной литературы.

Раздел 1. Теоретические аспекты использования системно-деятельностного подхода при изучении темы обыкновенные дроби

1.1. Сущность системно-деятельностного подхода

Базовым документом Концепции новых образовательных стандартов является программа развития универсальных учебных действий, призванная конкретизировать требования к результатам общего образования и дополнить традиционное содержание учебно-воспитательных программ. Необходимо оценивать готовность школьников к обучению на новой ступени образования не только и не столько на основе знаний, умений навыков, сколько на базе сформированности основных видов универсальных учебных действий. Основанием преемственности разных ступеней образовательной системы может стать ориентация на ключевой стратегический приоритет непрерывного образования — формирование умения учиться [4].

В действующих в настоящее время образовательных стандартах усилено внимание к формированию общеучебных умений и использованию приобретенных знаний и умений в практической деятельности и повседневной жизни. Однако этого не достаточно. Необходимо, сохраняя лучшие традиции российского образования, переориентировать его на новые образовательные результаты, отражающие не только освоение предметного содержания (знаний и умений, опыта творческой деятельности), но и овладение метапредметными умениями (способами деятельности, применимыми как в обучении, так и при решении проблем в реальных жизненных ситуациях), а также включающие личностные результаты (систему ценностных отношений, интересов, мотивации учащихся) [2].

В связи с тем, что приоритетным направлением новых образовательных стандартов становится реализация развивающего потенциала общего среднего образования, актуальной задачей становится обеспечение развития универсальных учебных действий как собственно психологической составляющей фундаментального ядра содержания образования. Поэтому важнейшей задачей является формирование совокупности универсальных учебных действий как метапредметных результатов образования.

В основе ФГОС лежит системно-деятельностный подход, который предполагает: ориентацию на результаты образования как системообразующий компонент Стандарта, где развитие личности обучающегося на основе усвоения универсальных учебных действий, познания и освоения мира составляет цель и основной результат образования [2].

Данный подход, концептуально базируется на обеспечении соответствия учебной деятельности обучающихся их возрасту и индивидуальным особенностям.

Понятие системно-деятельностного подхода было введено в 1985 г. как особого рода понятие. Этим старались снять оппозицию внутри отечественной психологической науки между системным подходом, который разрабатывался в исследованиях классиков отечественной науки (таких, как Б.Г.Ананьев, Б.Ф.Ломов и др.), и деятельностным, который всегда был системным (его разрабатывали Л.С.Выготский, Л.В.Занков, А.Р.Лурия, Д.Б.Эльконин, В.В.Давыдов и многие др.). Системно-деятельностный подход является попыткой объединения этих подходов [3].

Особенностью системно-деятельностного подхода является положение о том, что психологические функции и способности есть результат преобразования внешней предметной деятельности во внутреннюю психическую деятельность путем последовательных преобразований. При этом содержание образования проектирует определенный тип мышления ребенка – эмпирический или теоретический в зависимости от содержания обучения. Содержание же учебного предмета выступает как система научных понятий, конституирующих определенную предметную область. В основе усвоения системы научных понятий лежит организация системы учебных действий [5].

Системно-деятельностный подход приводит к пониманию того, чем являются в широком смысле слова стандарты образования. Такой подход не отрицает ЗУНовского подхода. На оперционально-технологическом уровне без ЗУНов ничего не получится. Вместе с тем, действует еще одна формула: компетенция — деятельность — компетентность. Компетенция как объективная характеристика реальности должна пройти через деятельность, чтобы стать компетентностью, как характеристикой личности. Эта формула помогает нам понять, что такое компетентность. Это знание в действии. И компетентностный подход не противостоит деятельностному, а снимается им.

Системно-деятельностный подход к результатам образования, означает, в частности, что изменяется представление о содержании образования. Его состав, в соответствии с принятым подходом к формированию стандарта и конкретизирующей его системой нормативных документов, определяется не только традиционной «ЗУНовской» составляющей, отражающей систему взглядов, идей, теорий, ключевых понятий и методов базовых наук, лежащих в основе школьных предметов, но и дополняется «деятельностной» составляющей, отражающей представления о структуре учебной деятельности на разных этапах обучения и при разных формах – индивидуальной или совместной – ее организации [3].

Системно-деятельностный подход позволяет на каждой ступени общего образования:

- представить цели образования в виде системы ключевых задач, отражающих направления формирования качеств личности;

- на основании построенных целей обосновать не только способы действий, которые должны быть сформированы в учебном процессе, но и содержание обучения в их взаимосвязи;

- выделить основные результаты обучения и воспитания как достижения личностного, социального, коммуникативного и познавательного развития учащихся.

Системно-деятельностный подход обеспечивает достижение планируемых результатов освоения основной образовательной программы начального общего образования и создает основу для самостоятельного успешного усвоения обучающимися новых знаний, умений, компетенций, видов и способов деятельности.

В целом системно-деятельностный подход в обучении означает, что в этом процессе ставится и решается основная задача образования — создание условий развития гармоничной, нравственно совершенной, социально активной, профессионально компетентной и саморазвивающейся личности через активизацию внутренних резервов. Для реализации системно-деятельностного подхода необходимо перейти от освоения отдельных учебных предметов к межпредметному изучению сложных ситуаций реальной жизни. Соответственно, специфические для каждого учебного предмета действия и операции должны быть дополнены универсальными (метапредметными) учебными действиями [10].

Таким образом, системно-деятельностный подход нацелен на развитие личности, на формирование гражданской идентичности, указывает и помогает отследить ценностные ориентиры, которые встраиваются в новое поколение стандартов российского образования.

1.2. Современный урок математики с позиции системно-деятельностного подхода

Системно-деятельностный подход – методологическая основа стандартов основного общего образования нового поколения. Системно-деятельностный подход нацелен на комплексное гармоничное развитие личности, на формирование индивидуальных способностей [13].

Так как основной формой организации обучения является урок, то необходимо знать принципы построения урока, примерную типологию уроков и критерии оценивания урока в рамках СДП [15].

СДП подразумевает системную организацию учебной деятельности школьников, в которой условно можно выделить три главные составляющие: мотивационно-целевой, этап (включают такие структурные компоненты учебной деятельности как учебно-познавательные мотивы и действие целеполагания), процессуальный этап (включает такие структурные компоненты учебной деятельности как планирование решения, решение задач) и рефлексивно-оценочный этап (включает рефлексивно-оценочные действия). Соответственно эти этапы должны быть отражены в структуре урока, спроектированного в формате СДП.

Мотивационно-ценностный этап характеризуется созданием ситуации в которой происходит положительное самоопределение ученика деятельности на уроке. Речь идет о создании таких условий, в которых возникает внутренняя потребность включения в деятельность. Отметим, что для ученика основной школы, в том числе и 5-6 класса главным видом деятельности является обучение в школе. Существенная особенность такой деятельности учеников 5-6 класса заключается избирательной готовности к тем или иным сторонам обучения. В этом плане высока роль мотивов. Ребенок такого возраста проявляет большую готовность к тем видам учебной деятельности, в которых он выглядит взрослым в собственных глазах. Наибольший интерес вызывают самостоятельные формы организации занятий на уроке, сложный учебный материал, возможность самому строить свою познавательную деятельность вне урока. Однако ребенок 5-6 класса не всегда осуществлять такую деятельность. Основная неудача учащихся в учебно-познавательной деятельности в таком возрасте связана несформированности у учащихся способов учебной деятельности, что не дает возможности реализовать актуальную потребность ученика данного возраста – потребность в самоутверждении. Естественно для повышения эффективности обучения учеников является целенаправленное формирование у них мотивов учения [1].

Процессуальный этап предполагает организацию деятельности учащихся по «открытию» нового знания и его применению.

Рефлексивно-оценочный этап связан с фиксированием освоенного содержания, изученного на уроке, с последующей рефлексией, самооценкой и взаимооценкой учениками деятельности на уроке. Устанавливается степень соответствия поставленной цели на первом этапе и результатов осуществленной деятельности, определяются цели последующей деятельности.

Отметим, что основу деятельности учеников 5-6 классов составляют мотивы. Это связано с психологическими особенностями данного возраста. Для этого возрастного периода важно наличие познавательного интереса, познавательной потребности. Кроме того, необходимо чтобы ученики осознавали для чего им нужны знания, освоенные на уроке, а также их содержание, оно должно быть интересным и жизненным. Только в таком случае обучение будет осознанным. Кроме того велика роль самооценки учащихся своих способностей и знаний [5].

Как видно из вышеизложенного, психические процессы характерные для учеников 5-6 классов, существенно влияют на процесс усвоения знаний и умений. Поэтому их учёт их необходим для организации успешного обучения учащихся. Соответственно данные факты нашли отражение и в организационной структуре урока в формате СДП.

Уроки деятельностной направленности по целеполаганию можно распределить на три группы:

1. уроки «открытия» нового знания;

2. уроки рефлексии;

3. уроки развивающего контроля [5].

Этапы каждого из видов урока повторяют этапы деятельности, выделенные нами в предыдущем параграфе. Поэтому структура любого урока в формате СДП содержит такие структурные этапы:

1. Мотивация (самоопределение) к учебной деятельности.

2. Актуализация и фиксирование индивидуального затруднения в пробном действии.

3. Постановка проблемы.

4. Построение проекта выхода из затруднения.

5. Реализация построенного проекта.

6. Первичное закрепление с проговариванием во внешней речи.

7. Самостоятельная работа с самопроверкой по эталону.

8. Включение в систему знаний и повторение.

9. Рефлексия учебной деятельности [6].

В нашем исследовании мы придерживаемся мнения, что для успешной реализации урока основанного на системно деятельностном подходе, необходимо провести тщательную его подготовку. В связи с этим логично обратиться к методическим вопросам проектирования таких уроков [8].

Поэтому в процессе подготовки урока в формате СДП мы предлагаем разрабатывать и использовать технологическую карту урока, которая содержит:

 название темы;

 планируемые результаты (личностные, метапредметные, предметные);

 тип урока (учебного занятия), определяющий технологию [6]

Учителю следует обратить внимание на следующие: разбиение учебного процесса на уроки разных типов в соответствии с ведущими целями не должно разрушать его непрерывность, а значит, необходимо обеспечить инвариантность технологии обучения. Поэтому при построении технологии организации уроков разных типов должен деятельностный метод обучения и обеспечиваться соответствующая ему система дидактических принципов как основа для построения структуры и условий взаимодействия между учителем и учеником.

Раздел 2. Методические аспекты реализации системно-деятельностного подхода при изучении темы обыкновенные дроби

2.1. Комплекс задач по теме «Обыкновенные дроби» при реализации системно-деятельностного подхода

1. Среди данных математических предложений выбрать те, которые сформулированы правильно.

Пример. Выберите правильную формулировку определения:

− неправильной называется дробь, у которой числитель больше знаменателя; (Л)

− правильной называется дробь, у которой числитель больше знаменателя; (Л)

− неправильной называется дробь, у которой числитель не меньше знаменателя; (И)

− правильной называется дробь, у которой числитель не больше знаменателя; (Л)

− неправильной называется дробь, у которой числитель равен знаменателю; (И)

− правильной называется дробь, у которой числитель меньше знаменателя; (И)

2. Решить задачу с недостающими (лишними, противоречивыми) данными, с необычной фабулой или постановкой вопроса.

Пример. Какие данные противоречивы?

− Дана правильная дробь, числитель которой кратен 3 а знаменатель равен 2. Найдите все такие дроби.

Пример. Измените условие задачи так, чтобы она имела единственное решение:

− В соревновании участвовало 140 спортсменов. В каждой команде было по 8 мужчин. Сколько всего было женщин, если в команде их было меньше, чем мужчин?

3. В 56-х классах, когда учащиеся еще только осваивают предложенную деятельность, учитель может быть инициатором первых (разных) версий решения проблемы.

Пример. Сравните несколько предложенных дробей.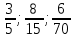



Удобно ли сравнивать эти дроби, применяя данный порядок действий? Чем он удобен? Предложите другой способ сравнения этих дробей, какие средства вам «подскажут» способ – справочник по математике, интернет-ресурсы или другие источники? Какие еще способы сравнения дробей вы обнаружили в используемом источнике? Приведите пример пары таких дробей, которые удобнее сравнивать, используя другой порядок действий.

4. Сформулировать задачу, аналогичную (обратную, частично измененную) данной типовой задаче.

Пример. Дана задача: в классе 24 ученика писали контрольную работу по математике. Сколько учеников справилось с работой на «отлично», если они составили 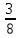от всего количества учащихся?

− прочитайте эту задачу;

− если в дайной задаче будет известно количество детей, не справившихся с контрольной работой, то можно ли ответить на вопрос задачи?

− придумайте задачу, которая решается по такому же алгоритму;

− придумайте задачу, обратную данной;

− как можно решить обратную задачу, используя приѐм решения данной?

5. Пример. Выполните деление столбиком десятичной дроби (придумайте сами) на 10, 100, 1000,. Составьте таблицу

Данн ое число	Результат деления на
	10	100	1000	10000

Проанализируйте получившиеся результаты, сформулируйте гипотезу о получившейся закономерности.

Пример. Выполните умножение десятичных дробей. Заполните таблицу, которая представлена выше. Сформулируйте правило умножения десятичных дробей.

6. Подобрать для соседа по парте задания определенного вида решения на этапе повторения и предложить ему их решить, организовать работу над ошибками. Оценка качества выполненной работы одноклассника.

Пример. Составить 10 заданий на последовательное процентное изменение величины:

• 
  двойное повышение на одно и то же число процентов;
  
• 
  двойное понижение на одно и то же число процентов;
  
• 
  двойное повышение на разное число процентов;
  
• 
  двойное понижение на разное число процентов;
  
• 
  повышение, а затем понижение на одно и то же число процентов;
  
• 
  понижение, а затем повышение на одно и то же число процентов;
  
• 
  повышение, а затем понижение на разное число процентов;
  
• 
  понижение, а затем повышение на разное число процентов.
  

7. Измените условие задачи так, чтобы она имела единственное решение:

− Числа, являющиеся числителем и знаменателем дроби, отличаются на 1 одно из этих чисел равно 7. Найдите эту дробь.

Для сравнения дробей с разными знаменателями чаще всего применяется следующий порядок действий:

− найти наименьшее общее кратное для чисел, стоящих в знаменателях дробей;

− найти дополнительные множители для знаменателей;

− умножить числитель и знаменатель каждой дроби на соответствующий дополнительный множитель; сравнить полученные числа.

2.2. Методы и приемы обучения, позволяющие реализовывать системно-деятельностный подход при изучении обыкновенных дробей

Классификация методов по характеру познавательной деятельности.

Объяснительно-иллюстративный метод, метод при котором преподаватель объясняет, а школьники воспринимают, осознают и фиксируют в памяти.

Репродуктивный метод (воспроизведение и применение информации)

Метод проблемного изложения (постановка проблемы и показ пути ее решения)

Частично – поисковый метод (студенты пытаются сами найти путь к решению проблемы)

Исследовательский метод (преподаватель направляет, студенты самостоятельно исследуют).

Наиболее продуктивным и интересным считаю создание проблемной ситуации, исследование, поиск правильного ответа.

Для развития познавательных интересов стараюсь выполнять следующие условия [9]:

1. 
   избегать в стиле преподавания будничности, монотонности, серости, бедности информации, отрыва от личного опыта студента;
   
2. 
   не допускать учебных перегрузок, переутомления и низкой плотности режима работы использовать содержание обучения как источник стимуляции познавательных интересов;
   
3. 
   стимулировать познавательные интересы многообразием приемов занимательности
   
4. 
   (иллюстрацией, игрой, кроссвордами, задачами-шутками, занимательными упражнениями т.д.);
   
5. 
   специально обучать приемам умственной деятельности и учебной работы, использовать проблемно-поисковые методы обучения.
   

Знания будут прочными, если они приобретены не одной памятью, не заучены механически, а являются продуктом собственных размышлений и проб и закрепились в результате его собственной творческой деятельности над учебным материалом.

Творческие, поисковые, проблемные задания позволяют создавать на уроках кратковременные педагогические ситуации для познавательной деятельности учащихся, обеспечивающих более полное включение их в самостоятельное выполнение.

На этапах «открытия» новых знаний важным становится организация самостоятельной деятельности учащихся, в процессе которой они выполняют проблемные и другие творческие задания (практические, лабораторные работы, проводят эксперимент). В результате этой деятельности получают «продукт» - вывод, определение понятия, формулировку математического предложения, выдвигают гипотезы, которые в дальнейшей работе проверяются, либо опровергаются. К проблемным заданиям можно отнести практическую и лабораторную работы, учебные исследования, основанные на эмпирических методах [14].

К творческим заданиям можно отнести занимательные задания и задачи, дидактические игры, творческие задания для самостоятельной работы при изучении нового материала, обобщения и систематизации. Выполняя творческие задания, ученик в большей степени становится субъектом учебной деятельности, вступает в диалог с учителем, активно участвует в познавательном процессе.

1) Занимательные задания и задачи

Под занимательностью на уроке понимают способы подачи учебного материала, специфические свойства информации и заданий, связанные с учебным материалом, с организацией обучения, если учебный материал содержит в себе элементы необычайного, удивительного, неожиданного, что вызывает интерес у школьников к учебному предмету и способствуют созданию положительной эмоциональной обстановки учения, способствует созданию нового.

Нередко занимательно сформулированная проблема вызывает потребность учащихся самостоятельно выдвигать математические идеи: необычный подход к рассмотрению проблемы, поиск ассоциаций, перенос идеи из другой области знаний.

Основу занимательности должны составлять задания, непосредственно связанные с изучаемым учебным материалом. Задания могут быть как репродуктивного, так и творческого, продуктивного характера. В методике математики выделяют три группы приемов занимательности и видов заданий (М.Ю. Шуба):

а) приемы занимательности, связанные с подачей задания;

б) приемы занимательности, связанные со структурой задания;

в) приемы занимательности, связанные с организацией и процессом решения.

С учетом воздействия занимательных заданий на мыслительную деятельность учащихся выделяют материалы, занимательные по форме; материалы, занимательные по содержанию; материалы, занимательные и по форме, и по содержанию. Видами занимательных заданий могут быть [14]:

- Занимательные вопросы, задачи, упражнения. Это такие задачи, в которой содержатся элементы занимательности либо в форме подачи задачи, либо в сюжете задачи, либо в способе решения, либо в иллюстративном материале к задаче. Эффективным в использовании занимательных заданий является включение в урок математических героев. Это может быть а) решение математическим героем какой-либо задачи и ответ его на вопрос; б) предложение математическим героем какой-нибудь задачи, которая по своему характеру занимательная; в) сообщение математическим героем по какой-либо учебной теме и включение учащихся в познавательную деятельность; г) предложение математическим героем для рассмотрения задания – ситуации, в которую он попал (делится своими знаниями, а учащиеся должны оценить правильность его действий и ответ); д) представление от лица математического героя учителем или одним из учеников задачи для анализа, поиска решения, решения задачи несколькими способами, выбора наиболее рационального способа решения задачи, самостоятельного составления других задач, в частности обратной и т.п.

- Практические работы занимательного характера. Это такой вид деятельности, в которой для выполнения задания необходимо проявить смекалку, применить хорошо усвоенные знания учебного материала и умения.

- Дидактические игры: игровая ситуация и математическая игра. Дидактическая игра выполняет на уроке те же функции, что и занимательное задание. В любой дидактической игре содержится проблема, элемент неожиданности и необычности. Дидактическая математическая игра характеризуется тем, что исход игры может быть предопределен предварительным теоретическим анализом, постановкой проблемы, выдвижением гипотезы.

Составление занимательных заданий требует от учителя совершенствования методики обучения, творческого использования занимательных заданий на уроках математики, освоение методов, средств и приемов подачи занимательных задач и занимательных форм организации обучения.

2) Творческие задания для самостоятельной работы при изучении нового материала, обобщения и систематизации

По возможности необходимо включить в урок одно или несколько особых творческих (но не репродуктивных) заданий. Такие задания должны быть направлены на совершенствование умений учащихся создавать нечто новое, используя свои знания и практические умения, жизненный опыт и интуицию. Большое значение имеет система заданий:

- задания, требующие воспроизведения данных (задания на узнавание; на воспроизведение отдельных фактов, понятий, определений, на повторение теорем, свойств, аксиом фигур, изучаемых объектов).

- задания, требующие простых мыслительных операций (на перечисление и описание фактов, алгоритмов, способов действий); на сопоставление и различение (сравнение, разделение на группы); на распределение (классификация); на выявление взаимоотношений между фактами (причина, следствие, функция, прямая и обратная теорема, признаки и свойства и др.);

- задания, требующие сложных мыслительных операций (на абстрагирование, конкретизацию, обобщение; задания на перенос, перевод, например, с одного языка на другой, с языка реальной речи на математический, или образный) задания на интерпретацию, разъяснения смысла или значения; задания на индукцию и дедукцию; задания на доказательство, аргументацию, проверку; задания на оценку (факта, явления, события);

- задания, требующие суммирования и обобщение (задания на составление проектов, докладов, рефератов, отчетов, выводов, формулировок теорем, математических предложений);

- задания, требующие творческого мышления; задания на практическое приложение знаний и применение умений; задания на решение проблемы (проблемного вопроса, проблемной задачи, выполнение проблемного задания).

Работа с математическим текстом и учебником – это вид деятельности по формированию информационных умений и способностей учащихся. В современных условиях ведущим направлением в обучении учащихся математике становится задача научить их работать с учебной математической книгой. Развитие умений работать с учебным математическим текстом (анализировать, извлекать необходимую информацию) является одним из предметных результатов освоения основной образовательной программы по математике для основной школы (из требований ФГОС основного общего образования).

В процессе обучения можно организовать самостоятельную деятельность учащихся с математическим текстом и учебником на разных этапах: особенно на этапах «открытия» новых знаний, на этапах обобщения и систематизации знаний, контроля и оценки. Для такой деятельности учащихся учителю необходимо составлять конкретные проблемные вопросы, проблемные задачи, проблемные задания. Примерами творческих заданий могут быть задания на установление истинности утверждений; на установление соответствия утверждений; задания на заполнение пропусков и дополнение в предложениях; на нахождение закономерностей; задания, в которых требуется анализировать и рассуждать. На этапах проверки усвоения изученных определений понятий эффективными становится задания на составление учащимися логических цепочек. Широко используются рисунки и чертежи, помогающие разобраться в соответствующих задачах и увидеть путь их решения [13].

Важнейшей задачей в основной школе становится обучение учащихся работать в соответствии с текстом, с указаниями в нем: последовательно выполнять те действия, которые рекомендуется выполнить в упражнении с одновременным прочтением текста учебника.

Стандартом определено формирование умений работать с информацией, представленной в форме таблиц и диаграмм, извлекать информацию из таблиц и диаграмм, составлять в ходе сбора необходимых данных таблицы и диаграммы, преобразовывать математический текст в наглядной форме в виде таблиц и диаграмм.

Заключение

Одним из возможных направлений повышения качества обучения учащихся основной школы на уроках математики, в рамках внедрения ФГОС, является системно-деятельностный подход. Организация процесса обучения через деятельность обучающихся, может служить основой для формирования у них творческого мышления.

Подтверждено, что повышению качества обучения математики способствует такое обучение, при котором на первый план выступает не сам процесс обучения, а овладение учащимися общей структурой деятельности, а именно теоретическим способом действия, состоящим из трех взаимосвязанных компонентов: анализа, планирования (внутреннего плана действия) и рефлексии.

В технологии СДП первым и основным критерием выбора методов, средств обучения, форм учебного процесса и учебной деятельности учащихся является уровень сформированности у учащихся приемов учебной деятельности. Приемы учебной деятельности должны составлять систему, адекватную системе учебного материала и системе учебных задач по его усвоению, а так же развитию и воспитанию учащихся средствами мтематики.

Современная школа должна направить свои усилия не на передачу готовых знаний, а на стимулирование поиска знаний, развитие умений применять эти знания на практике. Основная цель деятельностного подхода в обучении: научить не знаниям, а работе. Для реализации этой цели ставятся и решаются такие вопросы как: какой учебный материал отобрать и как подвергнуть его дидактической обработке; какие методы и средства обучения выбрать; как организовать собственную деятельность и деятельность учащихся.

Структура урока с позиций деятельностного подхода состоит следующем: учитель создает проблемную ситуацию; ученик принимает проблемную ситуацию; учитель управляет поисковой деятельностью; ученик осуществляет самостоятельный поиск; обсуждение результатов.

Библиографический список

1. 
   Антонов К.С. Современные проблемы методики преподавания математики. Сборник статей. Учебное пособие для студентов математических и физико-математических специальностей педагогических институтов. ‑ М.: Просвещение, 2018. – 166 с.
   
2. 
   Байденко В.И. Системно-деятельностный подход // Труды методологического семинара: проблемы, задачи, перспективы. - М.: Академия, 2018. - С. 25-30.
   
3. 
   Бермус, А.Г. Практическая педагогика. Учебное пособие. М.: Юрайт, 2020. ‑128 с.
   
4. 
   Далингер В.А. Системно-деятельностный подход к обучению математике // Наука и эпоха: монография / под ред. О.И. Кирикова. – Воронеж: Изд-во ВГПУ, 2019. – С. 230–243.
   
5. 
   Корбакова И.Н. Системно-деятельностный подход обучения. – Волгоград: Учитель, 2018. – 188 с.
   
6. 
   Кубышева, М.А. Реализация технологии системно-деятельностного метода на уроках разной целевой направленности. – М.: Просвещение, 2017. – 219 с.
   
7. 
   Лавриненко Г.А. Задания развивающего характера по математике / Г.А. Лавриненко. ‑ Саратов: Лицей, 2018. – 277 с.
   
8. 
   Петерсон Л.Г. Требование к составлению плана урока по дидактической системе деятельностного метода. – М.: Просвещение, 2016. – 117 с.
   
9. 
   Смолякова Д. В. Теория и методика обучения математике: учебно-методическое пособие. - Томск : Изд-во Томского гос. пед. ун-та, 2018. - 36 с.
   
10. 
    Сухов В.П. Системно-деятельностный подход в обучении. - СПб.: РГПУ им. А.И.Герцена, 2019. – 166 с.
    
11. 
    Темербекова, А.А. Методика преподавания математики / А.А. Темербекова. - М.: Владос, 2014. - 521 c.
    
12. 
    Тимофеева, И.Л. Вводный курс математики: Учебное пособие / И.Л. Тимофеева. - М.: Academia, 2019. - 163 c.
    
13. 
    Хуторской А.В. Системно-деятельностный подход в обучении – основа ФГОС. – М: Эйдос, 2018. – 253 с.
    
14. 
    Шаталов Г. Г. Способы повышения мотивации обучения // Математика: приложение к газете «Первое сентября». - 2019. - № 23. - С. 15-18.
    
15. 
    Юдин Э.Г. Системный подход и принцип деятельности. - М.: Наука, 2015. - 342 с.