Областное государственное автономное профессиональное образовательное учреждение Ютановский агромеханический техникум имени Е. П. Ковалевского
 Скачать 38.04 Kb. Скачать 38.04 Kb.
|
|
Областное государственное автономное профессиональное образовательное учреждение «Ютановский агромеханический техникум имени Е.П.Ковалевского» «Математические софизмы» (исследовательская работа по математике) Выполнил: обучающийся 1-го курса, специальности 10.06.2022 Контроль работы измерительных приборов Саенко Д. А Руководитель: преподаватель математики Степовая И.В. 2022 год Оглавление
ВВЕДЕНИЕ Великий ученый Исаак Ньютон говорил: «В математических вопросах нельзя пренебрегать даже самыми мелкими ошибками.» Думаю, многие из вас хоть раз в жизни слышали фразу: «Дважды два равно пяти». Подавляющее большинство людей размышляют и рассуждают, не обращаясь за помощью к науке, называемой логикой. Оказывается, некоторые заведомо ложные утверждения можно доказать. Такие утверждения называются софизмами. Софизмы - не самый важный раздел логики. Я решил поближе познакомиться с ними. В процессе работы я выяснил, что существует великое множество софизмов, и с их помощью можно доказать практически что угодно: как равенство всех чисел между собой, так и то, что прямой угол равен тупому. Обратился к теме софизмов я по нескольким причинам. Во-первых, считается, что именно софисты заставили задуматься о логическом строении геометрии и арифметики. Во-вторых, разбор софизмов сам по себе развивает навыки правильного мышления. В-третьих, это просто увлекательно. Эта тема сейчас актуальна. Каков бы ни был софизм, он обязательно содержит одну или несколько замаскированных ошибок. Разбор софизмов прежде всего развивает логическое мышление, т.е. прививает навыки правильного мышления. Обнаружить ошибку в софизме - это значит осознать ее, а осознание ошибки предупреждает от повторения ее в других математических рассуждениях. Важно добиться отчетливого понимания ошибок, иначе софизмы будут бесполезны. С помощью софизмов можно сделать уроки математики интересными и увлекательными. Цель моей работы: доказать, что софизмы являются не просто интеллектуальным мошенничеством, а важным двигателем человеческой мысли. Задачи: - изучить понятие софизмов; - выявить недостатки в истолковании софизмов; - выяснить, какие бывают софизмы в математике; -выяснить, какие основные ошибки допускаются в математических софизмах; - выявить роль софизмов в математике. Гипотеза: Каким бы ни был софизм, он всегда содержит одну или несколько замаскированных ошибок. Методы, используемые при проведении работы: изучение источников: литературы, энциклопедий, сайтов в Интернете; наблюдения, сопоставления; классификация и отбор материала; создание презентации. Понятие софизма. Исторические сведения Понятие софизма Софизм - формально кажущееся правильным, но по существу ложное умозаключение, основанное на преднамеренно неправильном подборе исходных положений. Софизм - (от греческого sophisma – уловка, ухищрение, выдумка, головоломка), умозаключение или рассуждение, обосновывающее какую-нибудь заведомую нелепость, абсурд или парадоксальное утверждение, противоречащее общепринятым представлениям. Каким бы ни был софизм, он всегда содержит одну или несколько замаскированных ошибок. Термин «софизм» впервые ввел Аристотель, охарактеризовавший софистику как мнимую, а не действительную мудрость. К софизмам им были отнесены и апории Зенона, направленные против движения и множественности вещей, и рассуждения собственно софистов, и все те софизмы, которые открывались в других философских школах. Это говорит о том, что софизмы не были изобретением одних софистов, а являлись скорее чем-то обычным для многих школ античной философии. Софизмы обычно трактуются вскользь и с очевидным осуждением. В обычном и распространенном понимании софизм - это умышленный обман, основанный на нарушении правил. Но обман тонкий и завуалированный, так, что его не сразу и не каждому удается раскрыть. Цель софизма – выдать ложь за истину. Считается, что прибегать к софизму предосудительно, как и вообще обманывать и внушать ложную мысль, зная, в чем заключается истина. Софизмы связывают с недостаточной самокритичностью ума и неспособностью сделать надлежащие выводы. Нередко софизм представляет собой просто защитную реакцию незнания или невежества, нежелающего признать свое бессилие и уступить знанию. В юриспруденции софизм традиционно считается помехой в споре. Использование софизмов уводит рассуждение в сторону: вместо выбранной темы приходится говорить о правилах и принципах логики. Вот пример древнего софизма: «Вор не желает приобрести ничего дурного; приобретение хорошего - есть дело хорошее; следовательно, вор желает хорошего». Стандартное истолкование софизма: Софизм - это мнимая проблема. Красивым примером «мнимой мудрости» является софизм «Электра»: В одной из трагедий Еврипида есть сцена, в которой Электра и Орест, брат и сестра встречаются после долгой разлуки. Знает ли Электра своего брата? Да она знает Ореста. Но вот он стоит перед ней непохожий на того, которого она видела в последний раз, и она не знает, что этот человек – Орест. Значит, она знает, то, что она не знает? Аристотель пытался разрешать подобные софизмы, ссылаясь на двусмысленность глагола «знать». Но ограничиваться только ссылкой на двусмысленность глагола не стоит. Важней другой вопрос: могут ли считаться истинными знания о предмете, если их не удается поставить в соответствие с самим предметом? Знание никогда не бывает полным, никогда не приобретает окончательных окостенелых очертаний. Введение новых, значимых элементов, нередко заставляет перестроить всю систему знания. Здесь фиксируется живое противоречие между наличием знания о предмете и опознанием этого предмета. О том, насколько важным является такое противоречие, говорит вся история теоретической науки и, в особенности, развитие современной высокоабстрактной науки. Поэтому, роль софизмов не однозначна. Первое неоспоримое достоинство софизмов – они заставили древних анализировать язык. Действительно, многие софизмы только выглядят как, лишенная смысла и цели, игра с языком. Игра, строящаяся на многозначности языковых выражений, их неполноте, зависимости значений от контекста, недоказанности и т.д. Все софические игры и шутки, увертливость в споре, склонность отстаивать самое нелепое положение, с одинаковой легкостью говорить «за» и «против» любого тезиса - все это только поверхность, за которой скрывается глубокое и серьезное содержание. Оно не осознавалось ни самими софистами, ни их противниками, включая Платона и Аристотеля, но оно очевидно сейчас. История возникновения софизмов Возникновение софизмов обычно связывается с философией софистов (Древняя Греция, V-IV вв. до новой эры), которая их обосновывала и оправдывала. Однако софизмы существовали задолго до философов-софистов, а наиболее известные и интересные были сформулированы позднее в сложившихся под влиянием Сократа философских школах. Процесс познания человеком окружающего мира можно сравнить с радостным торжеством, ибо каждая раскрытая тайна укрепляет веру в свои силы. Но на пути победоносной человеческой мысли возникают большие, казалось бы, непреодолимые, преграды, перед которыми умозаключения были бессильными. Древнегреческий философ Диодор Кронос (примерно 307 год до н.э.), не решив одну из древнейших логических задач – парадокс Эвклида, умер от разочарования, а другой философ Фигет Косский, познав такую же неудачу, покончил жизнь самоубийством. Древнегреческие ученые часто сталкивались с такими задачами в математике. Они прикладывали много усилий, чтобы выявить механизм образования подобных загадок. Было установлено, что наши рассуждения тоже подчинены определенным законам (законам логики), нарушение которых обесценивает результаты, добытые в этих рассуждениях. Неразрешенность задач, с которыми встретились Диодор Кронос и Фигет Косский, объясняется, как правило, нарушением законов логики. Поэтому уже тогда остро встал вопрос о системе «профилактических приемов» – определенных правил с целью устранения логических ошибок. Первая в истории проба проведения "логической профилактики" в математике принадлежит гениальному древнегреческому математику, автору «Начал» – Евклиду (IV в до н.э.). Он создал удивительный сборник «Псевдарий», где поместил разнообразные ошибочные рассуждения, к которым часто приходят те, кто начинает играть в математику. Таким образом, Евклид был автором первого из известных сборников математических софизмов и парадоксов. Остается сожалеть, что этот труд не дошел до нас. За то требовательность Евклида и строгость к культуре рассуждений нашла многочисленных последователей. Сами же софизмы также появились в Древней Греции. Они тесно связаны с философской деятельностью софистов — платных учителей мудрости, учивших всех желающих философии, логике и, особенно, риторике (науке и искусству красноречия). Однако софизмы существовали задолго до философов-софистов, а наиболее известные и интересные были сформулированы позднее в сложившихся под влиянием Сократа философских школах. Одна из основных задач софистов заключалась в том, чтобы научить человека доказывать (подтверждать или опровергать) все, что угодно, выходить победителем из любого интеллектуального состязания. Для этого они разрабатывали разнообразные логические, риторические и психологические приемы. К логическим приемам нечестного, но удачного ведения дискуссии и относятся софизмы. Однако, одних только софизмов для победы в любом споре недостаточно, ведь если объективная истина окажется не на стороне спорящего, то он, в любом случае, проиграет полемику, несмотря на все свое софистическое искусство. Это хорошо понимали и сами софисты. Поэтому помимо различных логических, риторических и психологических уловок в их арсенале была важная философская идея (особенно дорогая для них), состоявшая в том, что никакой объективной истины не существует: сколько людей, столько и истин. Софисты утверждали, что все в мире субъективно и относительно. Если признать эту идею справедливой, то тогда софистического искусства будет вполне достаточно для победы в любой дискуссии: побеждает не тот, кто находится на стороне истины, а тот, кто лучше владеет приемами полемики. Софистам идейно противостоял знаменитый греческий философ Сократ, который утверждал, что объективная истина есть, только неизвестно точно, какая она, что собой представляет; в силу чего задача каждого думающего человека заключается в том, чтобы искать эту единую для всех истину. Дискуссия между софистами и Сократом о существовании объективной истины зародилась приблизительно в V в. до н.э. С тех пор она продолжается до настоящего времени. Среди наших современников можно встретить немало людей, которые поддерживают софистов. "Сколько людей, столько и мнений", – говорят они. Однако и в нынешнюю эпоху есть те, которые вслед за Сократом считают, что, хотя мир и человек сложны и многогранны, тем не менее, нечто объективное и общезначимое существует, точно так же, как существует солнце в небе – одно для всех. В наше время ученые продолжают обращаться к софизмам совсем не для того, чтобы удивить кого-то. Человеку свойственно ошибаться, поэтому очень важно, чтобы он умел выявлять свои и чужие ошибки, учился избегать их. Действительно, чем хитрее софизм, чем искуснее замаскирована ошибка, тем больше удовлетворения приносит он тому, кто разгадал его, так как это – маленькое открытие и прекрасная школа культуры математических вычислений. 1.3 Софисты Изначально софистом называли каждого, кто отличался выдающимися познаниями или редкими умениями (например, Пифагора, семь мудрецов и натурфилософов). С середины V в. до н. э. так стали называть себя странствующие учителя мудрости. Однако насмешки староаттической комедии, а прежде всего диалоги Платона (Протагор, Горгий, Гиппий, Эвтидем) придали этому первоначально высокому определению уничижительное значение. Платон упрекал софистов в том, что они ищут не истины, а собственной славы и богатства (запрашивая высокие гонорары за индивидуальные или групповые занятия). Кроме этого, он критиковал их самовосхваление, болтливость и стремление победить противника любой ценой (не всегда при помощи корректных аргументов). Большая часть сочинений софистов утрачена. Сохранились только некоторые произведения Горгия, отрывки из Протагора, Двойные речи неизвестного автора и пара других фрагментов. Софисты были соединительным звеном между досократической натурфилософией и сократистами, занимавшимися этическими проблемами, но не составляли единой группы и часто расходились во взглядах. Сами они полагали, что занимают среднее положение между философами и политиками (Продик) или философами и риторами (Алкимад). Значение софистов не ограничивается их собственными достижениями, а основано на том, что они впервые поставили определенные вопросы, ответы на которые ищут по сей день. Влияние софистов было огромным. Во времена Римской Империи, особенно начиная со II в. н. э., понятие софистики приобрело новое значение (хотя софисты этой эпохи имели достаточно оснований полагать, что придерживаются традиций Горгия). Софистами часто называли риторов и учителей риторики, которая служила в основном для составления образцовых речей все более литературного характера. Этот период в истории греческой литературы называют второй софистикой. Этот термин появился впервые в Жизнеописаниях софистов Филострата (II), который и сам был софистом, представителем второй софистики. Другие ее представители - это прежде всего Дион Прусский, Герод Аттик, Элий Аристид, Максим Тирский, Лукиан. Поскольку риторика господствовала в школе, особенно в высшей, софистика играла чрезвычайно важную роль в культурной жизни. К наиболее выдающимся представителям поздней софистики принадлежат Либаний и Фемистий. Классификация математических софизмов Разбор и решение любого рода математических задач, а в особенности нестандартных, помогает развивать смекалку и логику. Математические софизмы относятся именно к таким задачам и подразделяются на алгебраические, геометрические, арифметические и логические. 2.1 Алгебраические софизмы Алгебраические софизмы – намеренно скрытые ошибки в уравнениях и числовых выражениях. Приведем некоторые примеры: Пять равно шести Попытаемся доказать, что 5=6. С этой целью возьмём числовое равенство: 35+10-45=42+12-54. Вынесем общие множители левой и правой частей за скобки. Получим: 5(7+2-9)=6(7+2-9). Разделим обе части этого равенства на общий множитель (заключенный в скобки). Получаем 5=6. В чём ошибка? 7+2-9=0. На ноль делить нельзя. Дважды два – пять Имеем числовое равенство (верное): 4:4=5:5. Вынесем за скобки в каждой части его общий множитель. Получим: 4(1:1)=5(1:1). Числа в скобках равны, поэтому 4=5, или х 2=5. Где ошибка? Ошибка сделана при вынесении общих множителей 4 из левой части и 5 из правой. Действительно, 4:4=1:1, но 4:4≠4(1:1). Отрицательное число больше положительного Возьмем два положительных числа а и с. Сравним два отношения: а и – а –с и с Они равны, так как каждое из них равно –(а/с). Можно составить пропорцию: а = –а – с = с Но если в пропорции предыдущий член первого отношения больше последующего, то предыдущий член второго отношения также больше своего последующего. В нашем случае а>– с, следовательно, должно быть –а>с, т.е. отрицательное число больше положительного. (Ошибка: данное свойство пропорции может оказаться неверным, если некоторые члены пропорции отрицательны). Сочетательное и переместительное свойства алгебраической суммы не имеют места Рассмотрим сумму бесконечного числа слагаемых, поочередно равных плюс единице и минус единице, т.е. S=1-1+1-1+1-1+1-1+1-1+…….. ,(1) И попробуем найти значение этой суммы. Сначала поступим следующим образом. Будем объединять слагаемые в пары, начиная со второго слагаемого, ставя перед каждой парой «минус», т.е. S=1-(1-1)-(1-1)-….=1-0-0-…=1. Теперь переставим каждое положительное слагаемое той же суммы (1) на место отрицательного и обратно, тогда S=-1+1-1+1-1+1-…=-1+(1-1)+(1-1)+…=-1+0+0+…=-1. Итак, по-разному переставляя слагаемые суммы(1), мы пришли к различным значениям этой суммы: 1 и –1, в итоге сумма слагаемых изменяется от перегруппировки слагаемых ,а сочетательное и переместительное свойства алгебраической суммы не имеют места. Где ошибка??? Данное свойство пропорции может оказаться неверным, если некоторые члены пропорции отрицательны. 2.2 Геометрические софизмы Геометрические софизмы – это умозаключения или рассуждения, обосновывающие какую-нибудь заведомую нелепость, абсурд или парадоксальное утверждение, связанное с геометрическими фигурами и действиями над ними. Через точку на прямую можно опустить два перпендикуляра Возьмем треугольник АВС. На сторонах АВ и ВС этого треугольника, как на диаметрах, построим полуокружности (Приложение 1). Пусть эти полуокружности пересекаются со стороной АС в точках Е и Д. Соединим точки Е и Д прямыми с точкой В. Угол АЕВ прямой, как вписанный, опирающийся на диаметр; угол ВДС также прямой. Следовательно, ВЕ перпендикулярна АС и ВД перпендикулярна АС. Через точку В проходят два перпендикуляра к прямой АС. Где ошибка??? Рассуждения, о том, что из точки на прямой можно опустить два перпендикуляра, опирались на ошибочный чертеж. В действительности полуокружности пересекаются со стороной АС в одной точке, т.е. ВЕ совпадает с ВD. Значит, из одной точки на прямой нельзя опустить два перпендикуляра. Катет равен гипотенузе 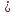 С = 90˚, ВД - биссектриса С = 90˚, ВД - биссектриса 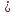 СВА, СК = КА, ОК СВА, СК = КА, ОК 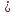 СА, СА,О - точка пересечения прямых ОК и ВД, ОМ 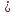 АВ, ОL АВ, ОL 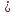 ВС. ВС.Имеем: 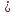 LВО = LВО = 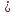 МВО, ВL = ВМ, ОМ = ОL = СК = КА, МВО, ВL = ВМ, ОМ = ОL = СК = КА,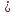 КОА = КОА =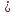 ОМА (ОА - общая сторона, КА = ОМ, ОМА (ОА - общая сторона, КА = ОМ, 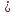 ОКА и ОКА и 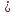 ОМА - прямые), ОМА - прямые),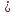 ОАК = ОАК = 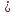 МОА, ОК = МА = СL, ВА = ВМ + МА, ВС = ВL + LС, но ВМ = ВL, МА = СL, и потому ВА = ВС МОА, ОК = МА = СL, ВА = ВМ + МА, ВС = ВL + LС, но ВМ = ВL, МА = СL, и потому ВА = ВС Где ошибка? Рассуждения, о том, что катет равен гипотенузе, опирались на ошибочный чертеж. Точка пересечения прямой, определяемой биссектрисой ВD и серединного перпендикуляра к катету АС, находится вне треугольника АВС. Софизм об исчезающем квадрате. Большой квадрат составлен из четырёх одинаковых четырёхугольников и маленького квадрата. Если четырёхугольники развернуть, то они заполнят площадь, занимаемую маленьким квадратом, хотя площадь большого квадрата визуально не изменится. Где ошибка? Посмотрим внимательно на ход действий. Одинаковая ли площадь у обоих квадратов? Нет, так как сторона и площадь нового квадрата меньше стороны и площади того, который был вначале. При решении данного софизма я воспользовался разрезанием этого квадрата, сложив части, и сравнив с исходным квадратом, получил, что он действительно становится меньше. 2.3. Арифметические софизмы Арифметические софизмы – это числовые выражения, имеющие неточность или ошибку, не заметную с первого взгляда. « Если А больше В, то А всегда больше, чем 2В». Возьмем два произвольных положительных числа А и В, такие, что А>В. Умножив это неравенство на В, получим новое неравенство А∙В>В·В, а вычитая из обеих его частей А·А, получим неравенство А∙В-А·А>В∙В-А·А, которое равносильно следующему: А(В-А)>(В+А)(В-А). (1) После деления обеих частей неравенства (1) на В-А получим, что А>В+А (2), А прибавив к этому неравенству по членно исходное неравенство А>В, имеем 2А>2В+А, откуда А>2В. Итак, если А>В, то А>2В. Это означает, к примеру, что из неравенства 6>5 следует, что 6>10. (Ошибка: здесь совершен неравносильный переход от неравенства (1) к неравенству (2)). Действительно, согласно условию А>В, поэтому В-А<0.Это означает, что обе части неравенства (1) делятся на отрицательное число. Но согласно правилу преобразования неравенств при делении или умножении неравенства на одно и то же отрицательное число знак неравенства необходимо изменить на противоположный. С учетом сказанного из неравенства (1) вместо неравенства (2) получим неравенство А<В+А, прибавив к которому почленно исходное неравенство В<А, получим просто исходное неравенство А+В<В+2А). «Число, равное другому числу, одновременно и больше, и меньше его». Возьмем два произвольных положительных равных числа А и В и напишем и напишем для них следующие очевидные неравенства: А> – В и В> – В. (1) Перемножив оба этих неравенства почленно, получим неравенство А·В>В·В, а после его деления на В, что вполне законно, ведь В>0, придем к выводу, что А>В. (2) Записав же два других столь же бесспорных неравенства В> – А и А> – А, (3) Аналогично предыдущему получим, что В·А>А·А, а разделив на А>0, придем к неравенству А>В. (4) Итак, число А, равное числу В, одновременно и больше, и меньше его. (Ошибка: здесь совершен неравносильный переход от одного неравенства к другому при недопустимом перемножении неравенств.) Проделаем правильные преобразования неравенств. Запишем неравенство (1) в виде А+В>0, В+В>0. Левые части этих неравенств положительны, следовательно, умножая по-членно оба эти неравенства (А+В)(В+В)>0, или А>– В, что представляет собой просто верное неравенство. Аналогично предыдущему, записывая неравенства (3) в виде (В+А)>0, А+А>0, получим просто верное неравенство В> – А. 2.4. Логические софизмы Логические софизмы - софизмы, ошибки которых заключаются в неправильных рассуждениях. Полупустое и полуполное «Полупустое есть то же, что и полуполное. Если равны половины, значит равны и целые. Следовательно, пустое есть то же, что и полное». Равен ли полный стакан пустому? Пусть имеется стакан, наполненный водой до половины. Тогда можно сказать, что стакан, наполовину полный равен стакану, наполовину пустому. Увеличивая обе части равенства вдвое, получим, что стакан полный равен стакану пустому. Не знаешь то, что знаешь «Знаешь ли ты то, о чём я хочу тебя спросить?» - «Нет». – «Знаешь ли ты, что добродетель есть добро?» - «Знаю». – «Об этом я и хотел тебя спросить. А ты, выходит, не знаешь то, что знаешь». Лекарства «Лекарство, принимаемое больным, есть добро. Чем больше делать добра, тем лучше. Значит, лекарств нужно принимать как можно больше». Вор «Вор не желает приобрести ничего дурного. Приобретение хорошего есть дело хорошее. Следовательно, вор желает хорошего». Рогатый «Что ты не терял, то имеешь. Рога ты не терял. Значит, у тебя рога». «Чем больше я пью водки, тем больше у меня трясутся руки. Чем больше у меня трясутся руки, тем больше спиртного я проливаю. Чем больше я проливаю, тем меньше я выпиваю. Значит, чтобы пить меньше, надо пить больше». Апельсин- планета Земля, Марс и т. д. - круглые. Значит, все планеты круглые. Апельсин тоже круглый, значит апельсин - планета? Сидящий стоит «Сидящий встал; кто встал, тот стоит; следовательно, сидящий стоит». Логический софизм Вход в парк некоего могущественного князя был запрещен. Если нарушитель попадался, его ожидала смерть, но ему предоставлялось право выбирать между виселицей и обезглавливанием. Он должен был что-то заявить, и если его утверждение было верно, его обезглавливали, а если ложно, то его вешали. Что нужно было заявить нарушителю, чтобы избежать установленного правила и остаться живым? «Меня повесят, естественно». Ты не человек Я человек, ты не я, значит ты не человек. ЗАКЛЮЧЕНИЕ Существует огромное множество разных видов софизмов. И те софизмы, что мы рассмотрели – всего лишь небольшая их часть. Из года в год появляются новые софизмы, некоторые из них могут остаться в истории, о многих быстро забудут. Ведь софизмы - это смесь математики и философии, поэтому они помогают не только развивать логику, но и лучше понимать математику в целом. В современном мире есть много людей, так или иначе употребляющих софизмы в обычной жизни, даже не зная, что это такое. Решение софизмов – интересное и познавательное занятие. Им можно заниматься как целенаправленно, так и в свободное время для собственного удовольствия. Благодаря софизмам можно научиться искать ошибки в рассуждениях других, научится грамотно строить свои рассуждения и логические объяснения. Когда ребенок раз притронется к горячему предмету, то впоследствии он постарается этого не делать. Он будет много осторожнее. Так и изучающий математику впоследствии проявит больше осторожности, чтобы не повторить осознанную ошибку. Значит, математические софизмы заставляют внимательно и настороженно продвигаться вперед, тщательно следить за точностью формулировок, правильностью записей и чертежей, за допустимостью обобщений, за законностью выполняемых операций. Все это нужно и полезно. Таким образом, я могу однозначно ответить на главный вопрос моей работы «Математические софизмы: заблуждение или путь к открытию?». Безусловно – путь к открытию. СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ Ахманов, А.С., Логическое учение Аристотеля, М., 1960г. Брадис, В.М., Минковский В.Л., Еленев Л.К., Ошибка в математических рассуждениях, 3 изд., М., 1967г. Глейзер, Г.И. История математики в школе. М.:Просвещение, 1982г. Кордемский, Б.А. Великие жизни в математике. М.:Просвещение, 1995г. |
