ИССЛЕДОВАНИЕ ДИНАМИКИ КОЛЕБАТЕЛЬНОГО И ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ. Обработка результатов. Обработка результатов
 Скачать 450.35 Kb. Скачать 450.35 Kb.
|
|
Обработка результатов 1. Определение по данным таблицы значения времен 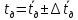 , ,  , ,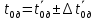 , , 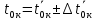 c P = 95% c P = 95%
Рассчитываем среднее значение по формуле:    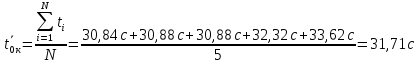 Рассчитываем СКО среднего по формуле: 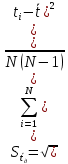  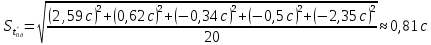  Рассчитываем случайную погрешность при N=5, tP,N=2,776, P=95%: 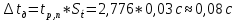 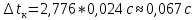  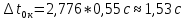 Рассчитываем приборную погрешность: 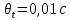 Рассчитываем полную погрешность: 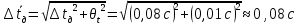 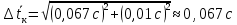 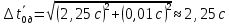 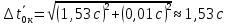 Окончательный результат: 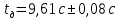 , P=95%, N=5 , P=95%, N=5 , P=95%, N=5 , P=95%, N=5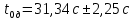 , P=95%, N=5 , P=95%, N=5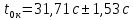 , P=95%, N=5 , P=95%, N=52. Расчёт периодов колебаний диска без кольца и с кольцом 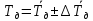 , ,  с P=95% : с P=95% : 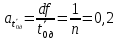 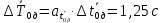 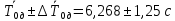 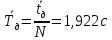  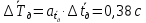 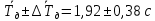 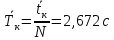 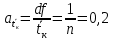 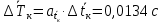 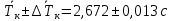 3. Рассчитаем время затухания маятника колебаний диска без кольца и с кольцом: 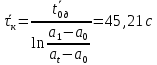 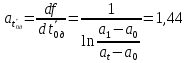  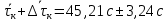  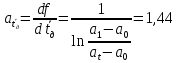 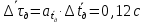 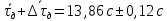 4. Рассчитаем собственные частоты колебаний маятника без кольца и с кольцом: 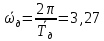 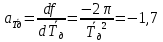 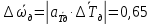 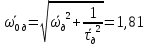 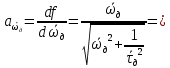 0,1 0,1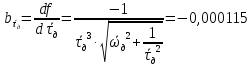   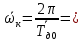 1 1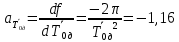 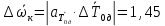 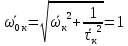 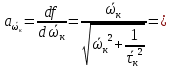 0,1 0,1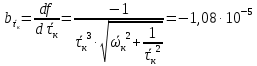 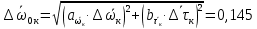 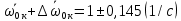 5. Рассчитаем момент инерции кольца:  6. Рассчитаем момент инерции диска: 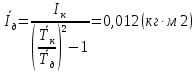 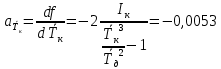  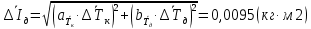 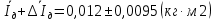 7. Рассчитаем значение момента инерции диска маятника исходя из его размеров и плотности материала: 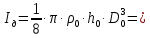 0,16(кг∙м2) 0,16(кг∙м2)8. Рассчитаем коэффициент кручения: 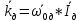  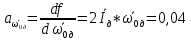 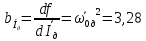  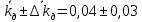 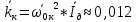 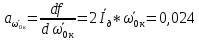 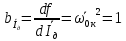   Рассчитаем среднее значение модуля сдвига G: 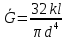  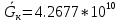 Рассчитаем модуль Юнга:  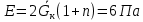 9. Определим полную энергию: 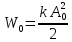 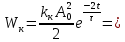  Определим мощность потерь: 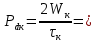 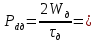 Определим добротность маятника: 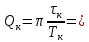 53 53 23 2310. В соответствии с уравнением затухающих колебаний постройте для маятника без кольца графики зависимости угла поворота маятника (t) и амплитуды A A(t) его колебаний от времени t.   Вывод Выполнив данную лабораторную работу, мы провели исследование динамики колебательного движения крутильного маятника. Во время этого исследования экспериментальным путем был получен ряд данных, на основании которых мы рассчитали период колебаний маятника без кольца и с кольцом, время затухания маятника, собственную частоту его колебаний, коэффициент кручения, модуль сдвига материала подвеса, а также определили полную энергию, мощность потерь и добротность маятника. В процессе выполнения данной работы выяснилось, что колебательная система характеризуется достаточно малой потерей энергии, что свидетельствует о хорошей её способности сохранять энергию. МИНОБРНАУКИ РОССИИ САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ЭЛЕКТРОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ «ЛЭТИ» ИМ. В.И. УЛЬЯНОВА (ЛЕНИНА) ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ №2 ПО ДИСЦИПЛИНЕ «ФИЗИКА» «ИССЛЕДОВАНИЕ ДИНАМИКИ СВОБОДНЫХ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ В ПОЛЕ СИЛЫ ТЯЖЕСТИ» Выполнил: Костюхина Э. В. Группа №: 0324 Преподаватель:
Санкт-Петербург 2021 Цель работы: изучение закономерностей колебательного движения тела в однородном поле силы тяжести; исследование процессов превращения энергии в консервативных системах; определение момента инерции физического маятника. Приборы и принадлежности: физический маятник; секундомер; масштабная линейка, чертежный треугольник. Конструкция оборотного маятника представлена на  рис. 2.1. На стержне 1 закреплены два диска –D1 и D2. Маятник может быть подвешен на кронштейне легкой призме, трение в которой пренебрежимо мало. рис. 2.1. На стержне 1 закреплены два диска –D1 и D2. Маятник может быть подвешен на кронштейне легкой призме, трение в которой пренебрежимо мало.Расчетные формулы: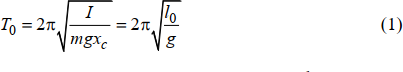 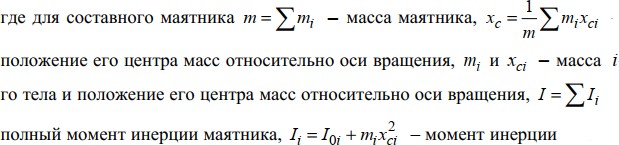  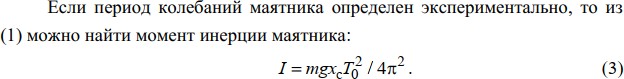   Гармонические колебания — колебания, при которых физическая величина изменяется с течением времени по гармоническому (синусоидальному, косинусоидальному) закону. при малых амплитудах можно приближенно заменить синус угла отклонения на сам угол, как это делается при выводе уравнения колебаний. Благодаря этой замене возвращающая сила оказывается пропорциональной углу отклонения, а это, в свою очередь, означает, что колебания являются гармоническими (то есть происходящими по синусоидальному закону) . Если не предполагать малости амплитуды, то возвращающая сила оказывается пропорциональной не самому углу, а его синусу. Такие колебания гармоническими не являются, и их математическое описание оказывается гораздо более сложным Физическим маятником называется твердое тело, закрепленное на неподвижной горизонтальной ocи (оси подвеса), не проходящей через центр тяжести, и совершающее колебания относительно этой оси под действием силы тяжести. В отличие от математического маятника массу такого тела нельзя считать точечной. Математическим маятником называется материальная точка массой m, подвешенная на невесомой нерастяжимой нити длиной L в поле силы тяжести (или других сил). Первая (скорость) и вторая (ускорение) производные по времени от гармонически колеблющейся величины s также совершают гармонические колебания с той же циклической частотой: 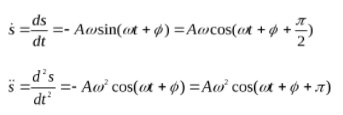  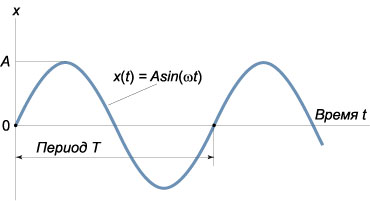 рис. 2.2 В этих формулах : A означает амплитуду колебаний, ωt + φ0 − фазу колебаний, φ0− начальную фазу в момент t=0. Величина ω называется круговой или циклической частотой колебаний. Она связана с периодом колебаний T соотношением ω=2*π/T. Из последнего уравнения видно, что s удовлетворяет уравнению  Это уравнение называется дифференциальным уравнением гармонических колебаний. Его решение: |
