задание 15 для подготовки к ЕГЭ. 17 ЕГЭeconom-s. Обучение методам решения задач с экономическим содержанием
 Скачать 142.19 Kb. Скачать 142.19 Kb.
|
|
Обучение методам решения задач с экономическим содержанием Задачи ЕГЭ №17 на кредиты обычно относятся к одному из двух характерных типов, которые легко различить между собой. 1 тип. Выплаты кредита производятся равными платежами. Эта схема еще называется «аннуитет» 2 тип. Выплаты кредита подбираются так, что сумма долга уменьшается равномерно. Это так называемая «схема с дифференцированными платежами» К первому типу относятся также задачи, в которых есть информация о платежах. Ко второму типу – задачи, в которых есть информация об изменении суммы долга. В задачах первого типа часто применяется формула суммы n членов геометрической прогрессии. В задачах второго типа – формула суммы n членов арифметической прогрессии. Рассмотрим основные подходы к решению нового типа задач ЕГЭ по математике – задач с «экономическим содержанием». Решение задач по формуле. Мы знаем, что если число А увеличить на р %, станет А(1+ 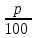 ).Если число А уменьшить на р %, станет А(1- ).Если число А уменьшить на р %, станет А(1-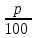 .) .)Цена товара А руб. была повышена на 25%. На сколько процентов надо теперь ее снизить, чтобы получить первоначальную цену товара. Решение:Цена товара после повышения стала А(1+ 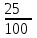 ). Допустим надо снизить на р %, тогда цена товара после снижения станет А(1+ ). Допустим надо снизить на р %, тогда цена товара после снижения станет А(1+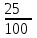 )(1- )(1-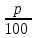 ) и получим первоначальную цену товара: А(1+ ) и получим первоначальную цену товара: А(1+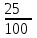 )(1- )(1-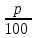 ) = А. Откуда получим ответ: 20% ) = А. Откуда получим ответ: 20%2.Банк под определенный процент принял некоторую сумму. Через год четверть накопленной суммы была снята со счета. Но банк увеличил процент годовых на 40%. К концу следующего года накопленая сумма в 1,44 раза превысила первоначальный вклад. Каков процент новых годовых? Решение:Положим в банк А рублей под р% годовых. Через год сумма на счету станет равной А(1+ 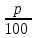 )рублей. Сняв четверть данной суммы, получим )рублей. Сняв четверть данной суммы, получим 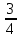 А(1+ А(1+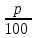 ). Теперь на эту сумму начисляют новый процент ). Теперь на эту сумму начисляют новый процент 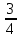 А(1+ А(1+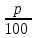 )(1+ )(1+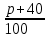 ), который стал 1,44А. Решив данное уравнение, получим ответ р=20%, тогда новый процент равен 60%. ), который стал 1,44А. Решив данное уравнение, получим ответ р=20%, тогда новый процент равен 60%.3.Фермер получил кредит в банке под определённый процент годовых. Через год фермер в счёт погашения кредита вернул в банк 3/4 от всей суммы, которую он был должен банку к этому времени, а ещё через год счёт полного погашения кредита он внёс в банк сумму, на 21% превышающую величину полученного кредита. Каков процент годовых по кредиту в данном банке? Решение: Допустим фермер получил А рублей под р% годовых. Через год долг будет А(1+ 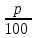 )руб. Т.к. фермер вернул )руб. Т.к. фермер вернул 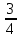 долга, то осталось долга, то осталось 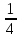 А(1+ А(1+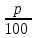 ). После 2-го года долг вырос на р% и стал ). После 2-го года долг вырос на р% и стал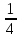 А(1+ А(1+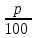 )А(1+ )А(1+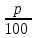 )= )=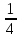 А(1+ А(1+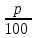 )2 .Теперь, чтобы погасить долг, фермер внес сумму на 21% большую, т.е. А(1+ )2 .Теперь, чтобы погасить долг, фермер внес сумму на 21% большую, т.е. А(1+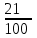 ) и погасил кредит, т.е ) и погасил кредит, т.е 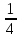 А(1+ А(1+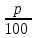 )2 - А(1+ )2 - А(1+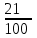 )=0. Решив данное уравнение, получим р=120%. )=0. Решив данное уравнение, получим р=120%.II. Некоторые задачи лучше решать в общем виде, не подставляя первоначальные данные, так как можно запутаться в вычислениях. 4. В банк помещена сумма 3900 тысяч рублей под 50% годовых. В конце каждого из первых четырех лет хранения после вычисления процентов вкладчик дополнительно вносил на счет одну и ту же фиксированную сумму. К концу пятого года после начисления процентов оказалось, что размер вклада увеличился по сравнению с первоначальным на 725%. Какую сумму вкладчик ежегодно добавлял к вкладу? Решение: пусть первоначальный вклад составил А рублей и вкладчик ежегодно добавлял х рублей. К началу 2-года величина вклада составила А (1+ 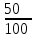 )= 1,5А рублей; )= 1,5А рублей;К началу 3-года величина вклада составила (1,5А +х)1,5+х рублей; К началу 4-года величина вклада составила ((1,5А +х)1,5+х)1,5+х рублей; К началу 5-года величина вклада составила (((1,5А +х)1,5+х)1,5+х)1,5+х рублей; К концу 5-года величина вклада составила((((1,5А +х)1,5+х)1,5+х)1,5+х)1,5 рублей. По условию задачи размер вклада увеличился по сравнению с первоначальным на 725% , т.е стал А(1+ 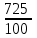 ). ).Раскрыв скобки, получим следующее выражение: ( 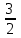 )5А+( )5А+(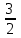 )4х+( )4х+(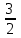 )3х+( )3х+(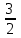 )2х+( )2х+(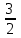 )х= )х=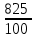 А= А=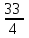 А А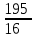 х= х=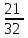 А АОтсюда, подставив вместо А=3900 тысяч, получим х=210000. III.Применение свойства степеней 5.За время хранения вклада в банке проценты по нему начислялись ежемесячно сначала в размере находился целое число месяцев, а по истечении срока хранения первоначальная сумма вклада увеличилась на Решение: Пусть первоначальная сумма вклада будет А рублей то через месяц эта сумма станет А(1+ 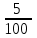 )руб. Если ставку не менять, то сумма увеличится опять на 5% и станет А(1+ )руб. Если ставку не менять, то сумма увеличится опять на 5% и станет А(1+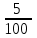 )2 и т.д. Пусть первая ставка продержалась k, вторая - m, третья - n, последняя - t месяцев. )2 и т.д. Пусть первая ставка продержалась k, вторая - m, третья - n, последняя - t месяцев. Тогда сумма увеличилась в А(1+ 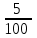 )к(1+ )к(1+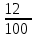 )m(1+ )m(1+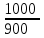 )n(1+ )n(1+ 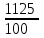 )t раз. И по истечении срока хранения первоначальная сумма стала А (1+ )t раз. И по истечении срока хранения первоначальная сумма стала А (1+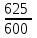 ) )А(1+ 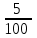 )к(1+ )к(1+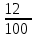 )m(1+ )m(1+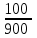 )n(1+ )n(1+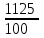 )t= )t=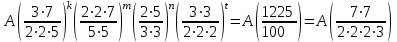 Применяя свойства степеней, получим Применяя свойства степеней, получим 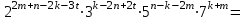 2 -3.3-1.50.72 2 -3.3-1.50.72приравнять показатели при одинаковых основаниях и решить систему: 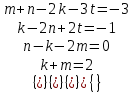 Откуда k=m=1. n=3, t=2. Тогда срок хранения вклада 1+1+3+2=7 месяцев. IV. Решение задач с помощью математического анализа 6.В январе 2000 года ставка по депозитам в банке «Возрождение» составляла х % годовых, тогда как в январе 2001 года — y % годовых, причем известно, что x+y=30%. В январе 2000 года вкладчик открыл счет в банке «Возрождение», положив на него некоторую сумму. В январе 2001 года, по прошествии года с того момента, вкладчик снял со счета пятую часть этой суммы. Укажите значение x при котором сумма на счету вкладчика в январе 2002 года станет максимально возможной. Решение:Пусть в январе 2000 года вкладчик открыл счет в банке на сумму А руб. Тогда через год при х % годовых на счету окажется сумма А (1 + 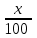 ) руб. ) руб.Далее вкладчик снимает со счета пятую часть первоначальной суммы. То есть на счету оказывается сумма 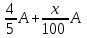 . В банке меняется процентная ставка и составляет теперь у %, т.е (30-х)%. Тогда еще через год у вкладчика на счету окажется . В банке меняется процентная ставка и составляет теперь у %, т.е (30-х)%. Тогда еще через год у вкладчика на счету окажется 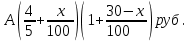 Нас интересует значение х, при котором значение f(x) = Нас интересует значение х, при котором значение f(x) =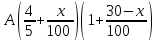 будет максимальным. Исследуем данную функцию методами математического анализа. будет максимальным. Исследуем данную функцию методами математического анализа. 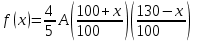 f/(x)=0 при 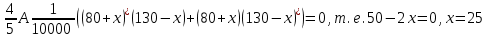 или Максимальное значение функция f(x) примет в точке х0 (вершина параболы), то есть в точке 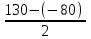 =25. =25.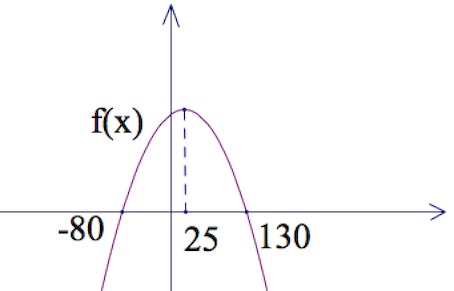 Ответ: 25%. V. Задачи на сравнение. 7.В конце августа 2001 года администрация Приморского края располагала некой суммой денег, которую предполагалось направить на пополнение нефтяных запасов края. Надеясь на изменение конъюнктуры рынка, руководство края, отсрочив закупку нефти, положила эту сумму 1 сентября 2001 года в банк. Далее известно, что сумма вклада в банке увеличивалась первого числа каждого месяца на 26% по отношению к сумме на первое число предыдущего месяца, а цена баррели сырой нефти убывала на 10% ежемесячно. На сколько процентов больше (от первоначального объема закупок) руководство края смогло пополнить нефтяные запасы края, сняв 1 ноября 2001 года всю сумму, полученную из банка вместе с процентами, и направив ее на закупку нефти? Решение:
Тогда сумма увеличится в 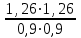 =1,96 , т.е. на 96% =1,96 , т.е. на 96%Ответ: на 96%.
| |||||||||||||||

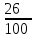 ) руб
) руб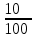 )руб
)руб