|
|
Алгебра_11 класс_Оценка числовых характеристик случайной величин. Оценка числовых характеристик случайной величины по выборочным данным
План урока
Раздел долгосрочного плана:
Раздел 11.1В: Элементы математической статистики
|
Школа:
|
Дата:
|
Имя учителя:
|
Класс: 11
|
Количество присутствующих:
|
Количество отсутствующих:
|
Тема урока: Оценка числовых характеристик случайной величины по выборочным данным
|
Тип урока
|
Урок изучения новой темы
|
Цели обучения (ЦО)
|
11.3.3.4 - оценивать числовые характеристики случайных величин по выборочным данным
|
Цели урока
|
Учащиеся оценивают числовые характеристики случайных величин по выборочным данным.
|
Критерии оценивания (КО)
|
Учащийся
понимает термин «несмещенная оценка»;
находит несмещенные оценки генеральной совокупности по выборочным данным.
|
Языковые цели
|
Учащиеся используют предметную лексику и терминологию раздела при оценке параметров генеральной совокупности.
Предметная лексика
генеральная совокупность и выборка; математическое ожидание, дисперсия, стандартное отклонение случайной величины; дисперсия, стандартное отклонение вариационного ряда; смещенная и несмещенная оценка.
Серия полезных фраз для диалога/письма
− на основе данных выборки вычисляют параметр выборки…
−… 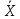 является несмещенной оценкой является несмещенной оценкой
−… выборочная дисперсия, является смещенной оценкой
- … оценивающая степень разброса случайной величины около математического ожидания.
|
Привитие ценностей
|
Привитие ценностей осуществляется посредством/через…
- ответственность;
- академическая честность;
- уважение;
- коммуникативные навыки
|
Межпредметные связи
|
Обработка данных при выполнении лабораторных работ по физике, химии, биологии
|
Навыки использования ИКТ
|
|
Предварительные знания
|
Знание элементов статистики: относительная частота, среднее арифметическое, дисперсия и стандартное отклонение вариационного ряда. Знание элементов теории вероятностей: классическое определение вероятности, определение математического ожидания, дисперсии и стандартного отклонения случайной величины. Числовые характеристики вариационных рядов, выборочное среднее, выборочная дисперсия и выборочное срднее квадратическое отклонение.
|
Ход урока
Запланированные этапы урока
|
Запланированная деятельность на уроке
|
Ресурсы
|
1 мин
|
Учитель знакомит учащихся с темой и целью урока, формулируя проблемный вопрос.
Учитель: «В теории вероятностей рассматриваются случайные величины с заданным распределением, свойства которых целиком известны, так как их можно вычислить.
В статистике часто эксперимент представляет собой черный ящик, выдающий лишь некие результаты, по которым требуется сделать вывод о свойствах самого эксперимента. Наблюдатель имеет набор числовых результатов, полученных повторением одного и того же случайного эксперимента в одинаковых условиях. При этом возникают, например, следующие вопросы: если мы наблюдаем одну случайную величину, то как по набору ее значений в нескольких опытах сделать как можно более точный вывод о ее распределении?»
|
Слайд
|
5 мин
|
Актуализация знаний. (Индивидуальная работа)
Ученикам следует выполнить соответствие между основными понятиями и определениями математической статистики (Приложение 1)
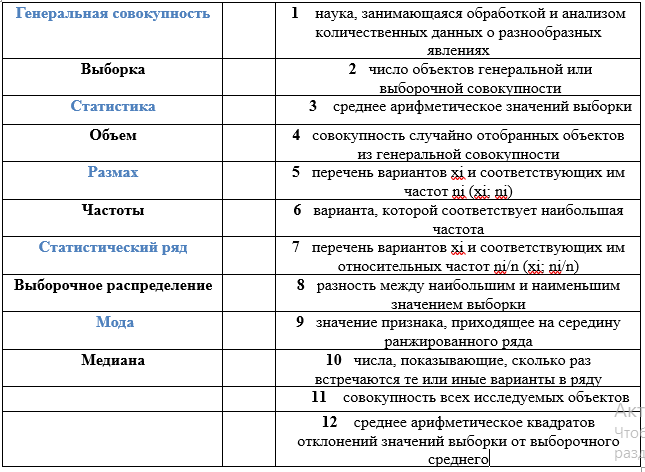
Ответ(Слайд презентации):
Затем ребята осуществляют самопроверку выполненного задания по правильному ответу учителя на интерактивной доске.
|
Приложение 1
|
10 мин
|
Изучение нового материала.
Учитель: «Вспомним основную задачу математической статистики. Она состоит в том, что для изучения генеральной совокупности объёма Nиз неё производится выборка, состоящая из n элементов, которая хорошо характеризует всю совокупность (свойство представительности). И на основании исследования этой выборочной совокупности мы с высокой достоверностью можем оценить генеральные характеристики. При работе с определениями у вас остались карточки, которые вы не использовали. Это выборочная средняя (выборочное математическое ожидание) и выборочная дисперсия. Найдите это определение запишите в тетрадь.».
Чаще всего требуется выявить закон распределения генеральной совокупности и оценить его важнейшие числовые параметры, такие как генеральная средняя 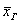 , генеральная дисперсия , генеральная дисперсия 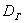 и среднее квадратическое отклонение и среднее квадратическое отклонение 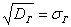 . .
Точечная оценка определяется одним числом.
Пусть значение оцениваемого параметра Ө, определенное по выборке, равно Ө*.
Точечная оценка называется:
несмещенной, если математическое ожидание Ө* равно Ө, т. е. М(Ө *) = Ө, это означает, что оценка не должна содержать систематической ошибки.
смещенной – в противном случае: М(Ө*) ≠ Ө.
Несмещенная оценка, имеющая минимальную дисперсию, называется эффективной.
Несмещенная оценка, дисперсия которой стремится к нулю при n  ∞ (n – объем выборки), называется состоятельной. ∞ (n – объем выборки), называется состоятельной.
Очевидно, что для оценки этих параметров нужно вычислить соответствующие выборочные значения. Выборочная средняя 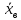 является несмещенной, состоятельной и эффективной для математического ожидания генеральной совокупности. является несмещенной, состоятельной и эффективной для математического ожидания генеральной совокупности.
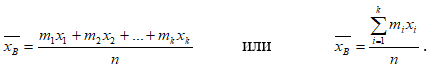
Аналогично, несмещённойи состоятельной точечной оценкой генеральной дисперсии 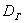 является исправленная выборочная дисперсия является исправленная выборочная дисперсия 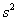 , , 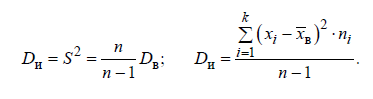
и соответственно, стандартного отклонения 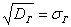 – исправленное стандартное отклонение s(эмперический стандарт). – исправленное стандартное отклонение s(эмперический стандарт).
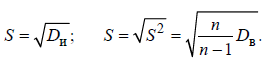
|
Слайд
|
7 мин
|
Первичное закрепление. (Весь класс)
Пример. Из генеральной совокупности взята выборка объема n=50:

Найти оценки параметров генеральной совокупности
(выборочное среднее 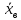 и исправленную дисперсию s2(x)). и исправленную дисперсию s2(x)).
Решение. Несмещенной оценкой генеральной средней есть выборочное среднее
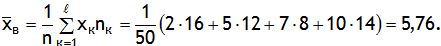
Для оценки генеральной дисперсии найдем величину исправленной дисперсии по формуле:
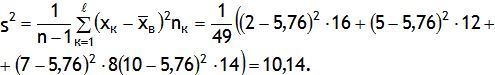
Оценку генеральной дисперсии можно находить по формуле:
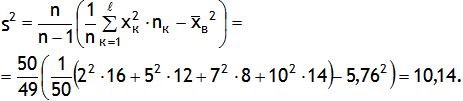
|
|
Слайд
|
15 мин
|
Решение задач. Парная работа
1. Из генеральной совокупности извлечена выборка
объема n = 50:
xi
|
2
|
5
|
7
|
10
|
ni
|
16
|
12
|
8
|
14
|
Найти несмещенную оценку генеральной средней.
Решение: Несмещенной оценкой генеральной средней является
выборочная средняя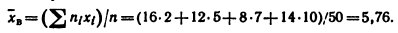
2.Выборочная совокупность задана таблицей распределения:
xi
|
0
|
1
|
2
|
3
|
4
|
ni
|
5
|
2
|
1
|
1
|
1
|
Найти выборочную среднюю, выборочную и исправленную дисперсию, среднее квадратическое отклонение.
Решение:n=10
Найдем выборочную среднюю:

 . .
Найдем выборочную дисперсию:


Найдем исправленную дисперсию:

 . .
Найдем среднее квадратическое отклонение:
 =1,37. =1,37.
Дескрипторы
знает понятие несмещенной оценки
находит выборочное среднее
находит выборочную и исправленную дисперсию
находит среднее квадратическое отклонение
Самооценивание по готовым ответам с использованием дескрипторов.
Учитель: «Были ли сложности с выполнением заданий? Что было легко, что было сложно?»
|
Приложение 2
|
5 мин
|
Формативное оценивание
Из генеральной совокупности извлечена выборка
объема n =60:
Найти несмещенную оценку генеральной средней.
Ответ: 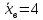 . .
2. Выборочная совокупность задана таблицей распределения:
xi
|
1
|
2
|
3
|
4
|
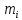
|
20
|
15
|
10
|
5
|
Найти выборочную дисперсию.
Ответ: 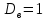 . .
Дескрипторы
знает понятие несмещенной оценки
находит выборочное среднее
находит выборочную дисперсию
Самооценивание по готовым ответам с использованием дескрипторов.
|
Приложение 3
|
2 мин
|
Рефлексия. Подведение итогов урока.
Учащимся предлагается ответить на вопросы, которые помогут учителю понять, насколько хорошо учащиеся усвоили изученный материал, над чем предстоит поработать на последующих уроках.
1) Что вам понравилось при изучении данной темы?
2) Что вы запомнили очень хорошо?
3) Что вызывало у вас сложность при изучении данной темы?
Домашнее задание: знать формулы нахождения несмещенных оценок
|
Слайд
|
Дифференциация
– каким образом Вы планируете оказать больше поддержки?
- какие задачи Вы планируете поставить перед более способными учащимися?
|
Оценивание
– как Вы планируете проверить уровень усвоения материала учащимися?
|
Здоровье и соблюдение техники безопасности
|
При постановке вопросов низкого и высокого порядка.
В ходе урока ребятам, в зависимости от испытываемых трудностей, оказывается дифференцированная поддержка.
|
Через достоверность ответов учащихся и качество выполнения письменных заданий.
|
Проветривание кабинета до начала урока.
Наблюдение за осанкой учащихся.
| |
|
|
 Скачать 150.08 Kb.
Скачать 150.08 Kb.