отчет. Оценка качества информации в сетях мобильной связи
 Скачать 0.53 Mb. Скачать 0.53 Mb.
|
|
Глава 3. РАСЧЁТНАЯ ЧАСТЬ 3.1 Показатели качества цифровых каналов связи Основным назначением каналов связи является передача информации. Исследуемые в данной работе широкополосные каналы связи предназначены для передачи данных, в частности мобильных, аудио- и видеосигналов. На качество передаваемого сигнала влияет множество факторов. К основным, наиболее широко изучаемым причинам снижения качества сигнала, относятся: искажение сигнала и снижение значения отношения сигнал/шум (SNR - Signal Noise Ratio). В теории связи к понятию сигнал относят видеоимпульс, информационный сигнал, или модулированную несущую. На снижение достоверности передачи аналоговых сигналов влияют так называемые интермодуляционные искажения (например, канальные искажения). Применительно к цифровым системам связи в основном используют понятие межсимвольной интерференции. В данной работе произведён расчёт вероятности появления битовой ошибки (BER - Bit Error Rate) в зависимости от заданного значения SNR [11]. По отношению к аналоговым сигналам критерием качества является показатель S/N (Signalto Noise), который определяет отношение средней мощности сигнала (S) к средней мощности шума (N). Для цифрового сигнала данный критерий обозначается как Eb/No (формула (1)). Здесь Eb - энергия бита, определяемая как произведение мощности сигнала S и времени передачи одного бита Tb; No - спектральная плотность мощности шума, которую можно выразить как отношение мощности шума N к ширине полосы пропускания W. Время передачи одного бита можно представить как 1/R, гдеR-битовая скорость, т.к. время и скорость передачи бита взаимно обратны: Для более наглядного выделения отношения сигнал/шум представим формулу (2) в следующем виде (формула (3)): 3.2 Расчёт показателей качества для многопозиционной модуляции Введём понятие метрики качества системы цифровой связи, которая представляет собой график зависимости вероятности появления ошибочного бита BEP (Bit Error Probability) от отношения Eb/No. В цифровых системах связи передача символов осуществляется в течение времени передачи одного символа - Ts. По отношению к одному информационному символу мощность находится в прямой зависимости от скорости передачи. Наиболее удобным параметром для описания цифрового сигнала является энергия, которую можно представить как мощность, проинтегрированную по времени. Поэтому для цифровых систем связи таким параметром является нормированный параметр Eb/No. На рисунке 19 представлен «водопадоподобный» вид большей части таких кривых при условии, что Eb/No≥Х0, РВ≤Р0, где Х0 - некоторый критерий отношения сигнал/шум для обеспечения удовлетворительной связи. Т.е. с увеличением значения требуемого отношения Eb/No повышается эффективность процесса детектирования при данной вероятности ошибки. 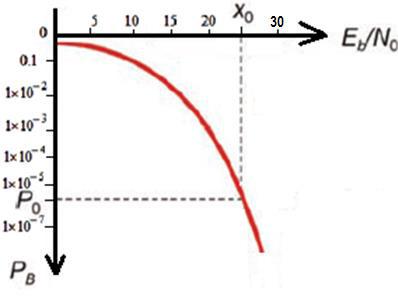 Рисунок 19 - Общий вид кривых зависимости вероятности ошибочно переданного бита к уровню Eb/No [12] Сравнение одной цифровой системы с другой должно производиться с помощью критерия качества на битовом уровне. Поэтому в цифровых системах наиболее удобно использовать параметр Eb/No, а не S/N, который незаменим для аналоговых систем связи. Поскольку понятие спектральной плотности мощности шума No описывает нормированный параметр Eb/No, подробнее опишем понятие мощности шума. В теории связи для описания модели случайного (хаотического) процесса чаще всего используется шум, который описывается гауссовским (нормальным) распределением. Шум возникает как результат одновременного воздействия нескольких независимых друг от друга случайных источников. Одним из примеров равномерного шума является тепловой шум, который обусловлен броуновским движением электронов в проводнике. Такой шум называется белым. Поскольку на входе приёмного устройства канала цифровой системы связи стоят фильтры, примем, что реальный белый шум соответствует идеальному. Шум ограничен по спектру, а значит, его мощность также конечна. Рассчитывая мощность N реального белого шума в полосе частот W (Гц), используется абсолютная температура источника шума Т, измеряемая в Кельвинах (К0 = С0 + 273) и спектральная плотность мощности шума, измеряемая в Вт/Гц:
Наибольшая мощность шума от теплового источника:
Зная, что энергия сигнала E = STo, а мощность шума N = NоW, где То - время передачи сигнала, получаю формулу (8): Величина WTo представляет коэффициент пересчёта отношения энергий сигнала и шума в отношение их средних мощностей. Число уровней амплитуд L при передаче цифрового сигнала с форматом модуляции M-КAM (QAM), где M представляет разрядность модуляции, определяется из формулы (9): Энергия символа сигнала определяется по формуле (10): В случае передачи в основной полосе частот многоуровневых импульсов, которые совпадают с полосой Найквиста, где WN = 1/2Tb, мощность символа и мощность шума определяются по формулам (11) и (12) соответственно: Таким образом, отношение сигнал/шум принимает вид: Формулу (13) можно преобразовать в вид: где m = 2(log2L) =log2M - коэффициент мапинга (число бит на символ информации). Таким образом, для сигналов с типом модуляции 16QAM разница между отношениями S/N и Eb/N0 составляет 6 дБ. Ещё одним показателем, характеризующим отношение мощностей, является отношение несущая/шум (C/N). Он определят, во сколько раз мощность С принимаемой модулированной ВЧ несущей на выходе приёмного фильтра больше мощности шума N. Ниже в формуле (15) указана зависимость: где При определении защитного отношения учитываются следующие параметры: шум, полоса частот, метод кодирования, а также значение коэффициента скругления, обозначенный на рисунке 20 (безразмерная величина, принимающая значения от 0,15 до 1) [12].  Рисунок 20 - Зависимость формы сигнала от коэффициента скругления Кроме того, для более точного расчёта отношения сигнал/шум в реальных условиях выведена корректирующая формула: где а – коэффициент скругления спектра. Формула пересчёта (16) выведена из расчёта, что реальная полоса шума для идеальной цифровой системы занимает полосу частот: а мощность несущей определяется как: Свёрточный код также оказывает влияние на канал связи. Коэффициент, корректирующий ошибки FEC (Forward Error Correction) принимает значения от 1/2 до 7/8. Чем он ниже, тем ниже скорость передачи данных. При значении FEC = 1/2, Eb/N0 снизится в 2 раза, т.е. на 3 дБ. Физический смысл данного примера заключается в том, что половина мощности сигнала уходит на FEC. Следовательно, значение Eb/No увеличивают на величину, равную 10lg(1/FEC) по отношению к C/N. Например, при скорости кодирования RC = 1/2 уровень FEC составит 3 дБ, при RC = 7/8 - 0,58 дБ. Однако, при RC = 1, FEC равен нулю. Для определения качества канала связи вводится два схожих понятия: вероятность появления битовой ошибки (BEP) и скорость появления битовой ошибки (BER). На практике удобнее использовать понятие BER, т.к. есть возможность физического измерения данной величины. 4.3 Расчёт вероятности битовой ошибки в канале связи технологии LTE При распространении в радиоэфире сигнал претерпевает различного рода изменения: искажения, снижение отношения сигнал/шум (SNR - Signal Noise Ratio). В цифровых системах радиосвязи используется обозначение Eb/N0 - отношение энергии одного бита к спектральной плотности шума, согласно формуле (14.14). Используя формулу пересчёта (17), можно легко вычислить показатель BER при заранее известном уровне SNR: где CR - скорость кодирования. Вероятность битовой ошибки в Гауссовском канале распространения имеет вид: 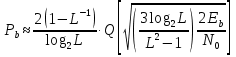 , (20) , (20)где Q(x) является табличной величиной, которая напрямую не рассчитывается. Однако, для х<3 значение параметра Q(x) можно рассчитать по формуле (14.12): Для минимизации расчётов на практике пользуются кривыми зависимости BER от SNR (Eb/N0), представленными в логарифмическом масштабе (рисунок 21). 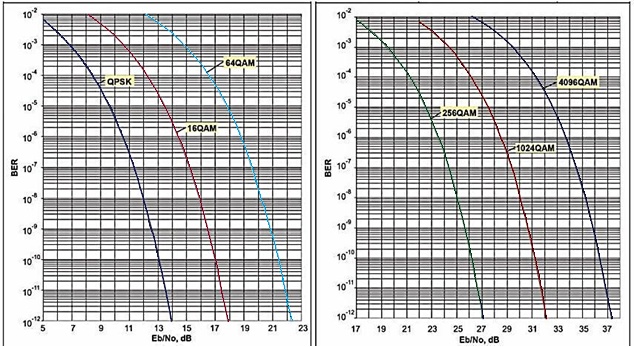 Рисунок 21 - Зависимости BER от Eb/N0 в логарифмическом масштабе Для подтверждения проведённого эксперимента рассчитываю вероятность появления битовых ошибок при заданном уровне отношения сигнал/шум. Необходимо подтвердить, что при использовании типа модуляции 64QAM при заданном значении SNR=18,9 дБ уровень BER не превышает 10-6. Для расчётов использую формулы (20) и (21):   (22) (22)Отсюда х=2/7 Перевожу значение отношения сигнал/шум в единицы: 18, 9дБ 101.89 78 Подставляю значение Q(x) и SNR для расчёта уровня BER:  (23) (23) (24) (24)Таким образом, из расчётов видно, что при данном значении SNR=18,9 дБ уровень BER соответствует требованиям качества к каналу связи технологии LTE. Аналогичный расчёт произведём для типа модуляции 16QAM при заданном SNR=13,5 дБ 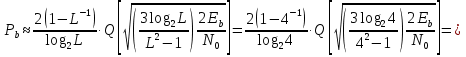 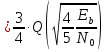 (25) (25)Отсюда х=4/5 Перевожу значение отношения сигнал/шум в единицы: 13, 5дБ 101.35 22, 4 Подставляю значение Q(x) и SNR для расчёта уровня BER: 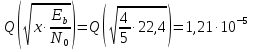 (26) (26) (27) (27)Таким образом, из расчётов видно, что при заданном значении SNR=13,5 дБ уровень BER также соответствует требованиям качества к каналу связи технологии LTE. Произведу сравнение результатов расчётов и результатов экспериментального моделирования, приведённых в таблице 5 (рисунки 22а, 22б). Таблица 5 - Зависимость BER от SNR по результат эксперимента и расчётов
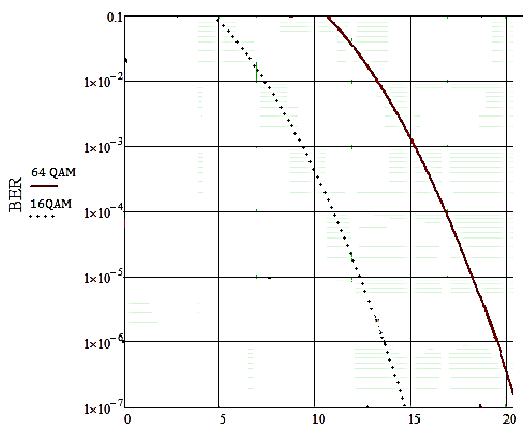 Рисунок 22а - Кривые зависимости BER от SNR, полученные в результате эксперимента  Рисунок 22б - Кривые зависимости BER от SNR, полученные в результате расчётов Погрешность результатов экспериментальных и расчётных данных составляет: Расхождение значений в 3-5% является допустимым. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
