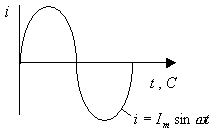5 лек ГД-22вв Омаров М.Б.. Одним из представителей переменного тока является синусоидальный ток
 Скачать 57.55 Kb.
|
|
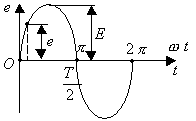
Одним из представителей переменного тока является синусоидальный ток. Переменными называются токи и напряжения, изменяющиеся во времени по величине и направлению. Его значение в любой момент времени носит название мгновенного значения. В качестве примера рассмотрим (рис.5.1): а) прямоугольный переменный ток 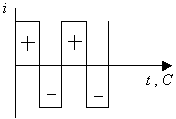 б) пилообразный ток 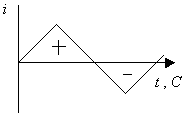 в) двухполупериодный переменный ток 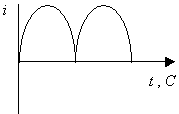 г) синусоидальный ток (периодический)
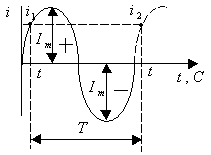
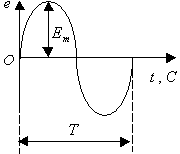
Наименьшее время, по истечении которого мгновенные значения периодически повторяются, называются периодом Т, тогда ток будет меняться  .Максимальное значение мгновенного тока называется амплитудой тока -  . Величина, обратная периоду, т.е. число периодов в единицу времени, называется частотой (линейной)  .Если все сказанное выше подытожить, то приходим к выводу: переменные электромагнитные процессы в электрических цепях происходят от синусоидального источника питания. Если источник напряжения синусоидальный, то и все токи на участках линейной цепи тоже будут синусоидальными (рис.4.2).
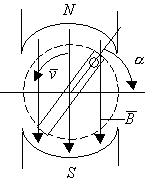
Аналитически они могут быть описаны  ,где  -скорость изменения аргумента (угла) называется угловой частотой, она равна  ПОЛУЧЕНИЕ СИНУСОИДАЛЬНОГО ТОКА И ЭДС Пусть в однородном магнитном поле NS (рис.4.4) равномерно вращается рамка, активные стороны которой a и b, расположенные перпендикулярно к плоскости чертежа и пересекающие линии магнитной индукции, движутся с некоторой линейной скоростью  . При этом в них будут наводится ЭДС по закону Фарадея и по правилу правой руки. где  ,  -среднее значение индукции.
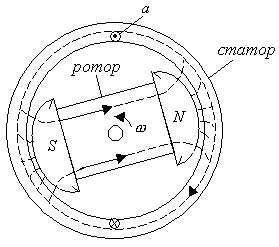
Для данной рамки  и при   - амплитуда ЭДС.Так как  ;  -фаза колебания,Т-период, -частота. (От частоты зависят потери в сердечниках и проводах).Наиболее оптимальная частота 50-60 Гц.  можно получить, используя закон Ома  .Синусоидальную ЭДС можно получить и другим способом. На современных электростанциях электрическая энергия получается от генераторов переменного тока, приводимых в движение механическими двигателями (преимущественно паровыми и гидравлическими турбинами ). Работа электромагнитных генераторов основана на законах электромагнитной индукции и электромагнитных сил. Генератор переменного тока (рис.4.5) состоит из двух основных частей – вращающегося ротора и неподвижного статора. На роторе расположены полюсы, т.е. электромагниты, обмотка которых питается от источника постоянного тока относительно небольшой мощности. Полюса создают магнитный поток машины. На цилиндрическом статоре расположена в пазах основная обмотка генератора, в которой индуцируется переменная ЭДС. На рис.4.5 показана схема устройства двухполюсного генератора синусоидального тока
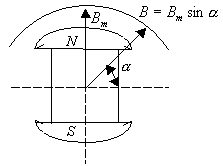
Сердечники статора и ротора изготовляют из стали. Магнитный поток Ф машины проходит через ферромагнитный материал на всем своем пути, за исключением двух небольших воздушных промежутков (зазоры), отделяющих ротор от статора. При вращении ротора с постоянной угловой скоростью в каждом проводнике статорной обмотки наводится по закону Фарадея ЭДС  ,где активная длина проводника  и линейная скорость перемещения магнитного поля остаются в процессе работы генератора неизменными. Характер изменения ЭДС  определяется законом распределения магнитной индукции  в воздушном зазоре машины.Для получения синусоидальной ЭДС полюсному наконечнику, обращенному к статору, придают такое очертание, при котором воздушный зазор увеличивается от середины полюса к его краям. Благодаря неравенству магнитных сопротивлений в различных частях воздушного зазора магнитная индукция имеет максимальные значения у середины полюса, где воздушный зазор минимален. По мере приближения к краям каждого полюса магнитная индукция постепенно убывает по закону синуса (рис.4.6). Момент, когда вращающийся ротор займет горизонтальное положение, примем за начало отсчета времени t=0 (рис.4.7, а). В месте расположения проводников а и b магнитная индукция В=0, поэтому индуцируемая в этих проводниках ЭДС  .В произвольный момент времени t, когда ротор повернется на угол 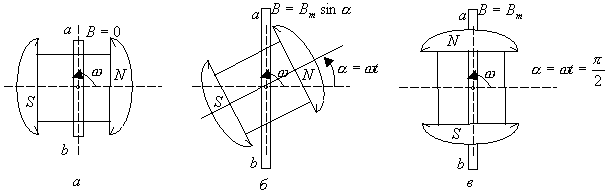 (рис.4.7,б), магнитная индукция в месте расположения проводников а и b будет равна  . В этих проводниках индуцируются одинаковые по величине ЭДС  . Рис. 5.7
 (1) Наибольшее значение ЭДС будет в витке при  (рис. 5.7,в) (2) Исходя из формул (1) и (2) и учитывая, что получаем (3)
ЭДС, наводимая в одном витке, относительно невелика. Для получения значительных ЭДС статорную обмотку выполняют из большого числа последовательно соединенных витков. ДЕЙСТВУЮЩИЕ ЗНАЧЕНИЯ ТОКА, НАПРЯЖЕНИЯ И ЭДС При расчете цепей переменного тока и их экспериментальном исследовании чаще всего пользуются понятием действующих значений тока, напряжения и ЭДС. Действующее значение переменной величины равно значению такого эквивалентного постоянного тока который, проходя по цепи с тем же сопротивлением, что и переменный ток, выделяет за период то же количество тепла. При сопротивлении цепи 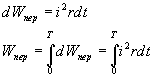 количество тепла, выделенное переменным током за бесконечно малый промежуток времени  :  Приравняв 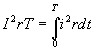 количеству тепла, выделенному при том же сопротивлении постоянным током  за то же время Т ,откуда действующее значение переменного тока 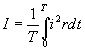 На рис.4.9 показаны переменный ток и квадрат переменного тока и эквивалентный ему постоянный ток 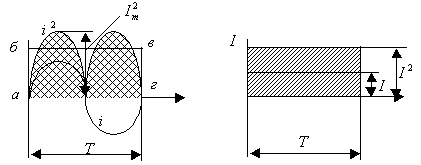 Рис. 5.10 Аналогично действующие значения напряжения и ЭДС имеют вид 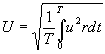 ;  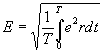Если ток изменяется по закону 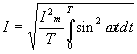, то действующее значение тока Так как 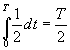 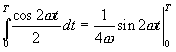и  ,  = 0получим:   ;  |
- функция синусоидальная
) и уравнение тока будет
, 
,определяющая стадию изменения синусоидального тока называется фазовым углом или фазой.
