ВВЕДЕНИЕ. Однократные измерения

• Название: Однократные измерения
• Дата: 12.03.2023
• Размер: 158.38 Kb.
• Имя файла: ВВЕДЕНИЕ.docx
• Тип: Документы; #983133

ВВЕДЕНИЕ

В наиболее широком смысле к "измерениям" относят обнаружение наличия или отсутствия каких-либо свойств, качественную оценку любого свойства, сопоставление величин с нормами, оценку свойства по косвенным показателям и ряд других действий. В отличие от геометрии, социометрии, антропометрии, и квалиметрии, имеющей наиболее широкий набор объектов оценки, метрология занимается измерениями физических величин. Потому мы не будем рассматривать получение экспертных оценок, а сосредоточимся только на измерениях тех параметров, которые подлежат объективной оценке с использованием средств измерений. Такие параметры в большинстве представляют собой физические величины, а их экспериментальные оценки называют аппаратурными или инструментальными в отличие от экспертных (органолептических) оценок, при получении которых инструментарием являются чувства человека.

Однократные измерения

Большинство технических измерений являются однократными. В производственных условиях их точность может быть вполне приемлемой, а простота и высокая производительность ставят однократные измерения вне конкуренции. При однократных измерениях процедура измерений регламентируется заранее, с тем чтобы при известной точности СИ и условиях измерения погрешность не превзошла определенное значение, т.е. значения А и Р заданы априори. Так как такие измерения выполняют без повторений, то нельзя отделить случайные погрешности от систематических. Для оценки погрешности дают лишь ее границы с учетом возможных влияющих величин.

Однократные измерения возможны при следующих условиях [8,19]:

• 
  — объем априорной информации об объекте измерений такой, что однократные измерения не вызывают сомнений;
  
• 
  — изучен метод измерения, его погрешности либо заранее устранены, либо оценены;
  
• 
  — метрологические характеристики СИ соответствуют установленным нормам.
  

При однократных измерениях возможно образование инструментальной, методической и субъективной погрешностей. Если последние две погрешности не превышают 15% погрешности СИ, погрешность измерения принимают равной погрешности используемого СИ [19J. Такая ситуация весьма часто имеет место на практике.

Как и при многократных измерениях, однократный отсчет показаний может содержать промах. Во избежание промаха при выполнении однократных измерений рекомендуется повторять измерения 2—3 раза, приняв за результат среднее арифметическое. Статистической обработке эти измерения не подвергаются. В простейшем случае если влияющие величины соответствуют нормальной области значений, погрешность результата прямого однократного измерения равна основной погрешности СИ Д_си, определяемой по нормативно-технической документации. Тогда результат измерения записывают в виде



где х_си — результат (среднее арифметическое значение из двух — трех

единичных измерений), зафиксированный СИ;

Р — доверительная вероятность (как правило, составляет 0,95).

При проведении измерений в условиях, отличных от нормальных, необходимо определять и учитывать пределы дополнительных погрешностей, вызванных этими отличиями (см. подп. 4.6.2).

Многократные прямые измерения

Обработка результатов многократных измерений согласно ГОСТ 8.207—76 «ГСИ. Прямые измерения с многократными наблюдениями. Методы обработки результатов наблюдений. Основные положения» заключается в нахождении результата измерения ФВ и доверительного интервала, в котором находится ее истинное значение.

Исходной информацией для обработки является ряд из п(п > 4) результатов единичных измерений х_ь х₂, х₃,х_п, из которых исключены известные систематические погрешности. Число измерений зависит от требований к точности получаемого результата и от реальной возможности выполнения повторных измерений.

Последовательность обработки результатов многократных измерений включает следующие этапы:

• 
  1) исключение из результатов измерений известных систематических погрешностей;
  
• 
  2) вычисление среднего арифметического значения х измеряемой величины из п единичных результатов;
  
• 
  3) вычисление средней квадратической погрешности единичных измерений в ряду измерений S_x;
  
• 
  4) исключение промахов (грубых погрешностей измерений);
  
• 
  5) вычисление средней квадратической погрешности результата измерений среднего арифметического S_x;
  
• 
  6) проверку гипотезы о принадлежности результатов измерений нормальному закону;
  
• 
  7) вычисление доверительных границ случайной погрешности результата измерений ±е;
  
• 
  8) вычисление доверительных границ неисключенной систематической погрешности результата измерений ±0;
  
• 
  9) вычисление доверительных границ погрешности результата измерений ±Д;
  
• 
  10) представление результата измерения в виде А = х±А, Р (Р — доверительная вероятность).
  

Известные систематические погрешности исключают введением в результат измерений соответствующих поправок, численно равных систематическим погрешностям, но противоположным им по знаку (см. подп. 4.4.3). Поправку вводят в результаты единичных измерений, а если известно, что результаты всех единичных измерений имеют одинаковые систематические погрешности, ее исключают из среднего арифметического значения измеряемой величины.

Среднее арифметическое значение измеряемой величины из п единичных результатов х определяют по формуле (4.22).

Для определения средней квадратической погрешности единичных измерений в ряду измерений S_x используют формулу (4.24).

Промахи (грубые погрешности измерений) могут сильно исказить результат измерений, поэтому их исключение из ряда измерений обязательно. Методика исключения промахов приведена в подп. 4.4.5.

Среднюю квадратическую погрешность результата измерений среднего арифметического значения S_x определяют по формуле (4.25).

Гипотезу о принадлежности результатов измерений нормальному закону проверяют с помощью критериев со² или %², если число измерений п > 50; если 15 < п < 50, используют составной критерий [8]. При п < 15 гипотезу о нормальном законе распределения результатов измерений не проверяют, предполагая, что вид закона распределения (нормальный) известен заранее [18, 19].

При заданном значении доверительной вероятности Р и числе единичных измерений п по таблицам (например, по табл. 4.9) определяют коэффициент Стьюдента t_p.

Таблица 4.9

Значения коэффициента Стьюдента t_p (ГОСТ 8.207—76)

	п
р	2	3	4	5	6	7	8	9	10	15
0,95	12,706	4,303	3,182	2,776	2,571	2,447	2,365	2,306	2,262	2,145
0,99	63,657	9,925	5,841	4,604	4,032	3,707	3,499	3,355	3,250	2,977

Доверительные границы случайной погрешности результата измерений определяют по формуле



Доверительные границы неисключенной систематической погрешности измерения, если можно выделить ее составляющие 0_У, определяют по формуле



где к — коэффициент (табл. 4.10), определяемый принятой доверительной вероятностью Р и числом т составляющих неисключенной систематической погрешности;

Qj — границыу-ой составляющей этой погрешности.

Таблица 4.10

Значения коэффициента к (ГОСТ 8.207—76)

	т
р	5 и более	4	3	2
0,95	U
0,99	1,45	1,40	1,30	1,20

Доверительную вероятность для вычисления границ неисключенной систематической погрешности принимают той же, что и при вычислении доверительных границ случайной погрешности результата измерения.

В соответствии с ГОСТ 8.207—76, суммирование неисключенной систематической и случайной погрешностей измерения осуществляют по следующим правилам.

1. Если отношение 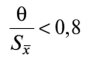 то неучтенной систематической погрешностью по сравнению со случайной погрешностью пренебрегают^[1] и принимают, что доверительные границы погрешности результата измерения Д = е.

2. Если отношение 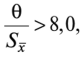 то случайной погрешностью по сравнению с неучтенной систематической пренебрегают^[1] и принимают, что доверительные границы погрешности результата измерения Д = 0.

3. Если 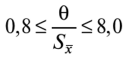 то доверительные границы погрешности результата измерений вычисляют по формуле



где К — коэффициент, зависящий от соотношения случайной и не-

исключенной систематической погрешности;

— суммарная средняя квадратическая погрешность результата измерений: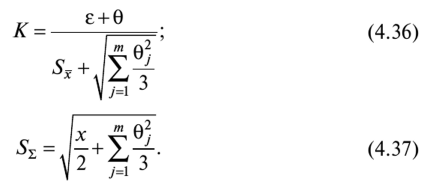



Если составляющие неисключенной систематической погрешности не установлены, а величина е соизмерима с абсолютным значением погрешности СИ Д_си, то величину Д_си считают неисключенной систематической погрешностью и в качестве доверительных границ погрешности результата измерений принимают величину [8J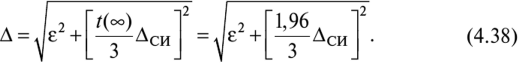



Окончательный результат записывают в виде А = х ± Д, Р, выполняя округление результатов расчета по правилам, изложенным в подп. 4.4.6.

При отсутствии данных о законах распределения погрешностей измерения результат измерения представляют в виде А = х; S_x, п 0, Р.

При обработке многократных прямых неравноточных измерений (измерений одной и той же величины, выполненных с различной точностью, различными приборами, различными операторами и т.д.) нельзя просто вычислять среднее арифметическое, поскольку это привело бы к увеличению погрешности за счет измерений, выполненных недостаточно тщательно или с недостаточной точностью.

При вычислении среднего арифметического неравноточных измерений предпочтение следует отдавать измерениям, выполненным с наибольшей точностью. Для этого каждому результату приписывают определенный «вес», т.е. число, характеризующее степень доверия к тому или иному отдельному результату измерений, входящему в ряд неравноточных измерений.

Тогда при неравноточных измерениях с «весами» результатов равноточных измерений g, в качестве результата принимают среднее взвешенное значение величины, определяемое по формуле



где Xj — среднее арифметическое ряда равноточных измерений: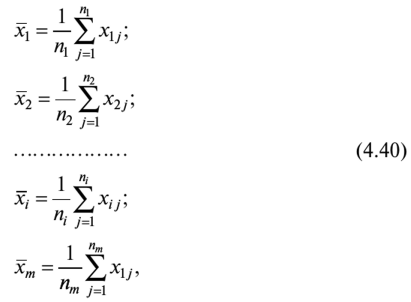



где Xj — единичное измерение в ряду равноточных измерений (/' = 1,

2,...,//);

п_ь п₂,..., п_т — число измерений в /-м ряду равноточных измерений (/ = 1,

2,

т — число рядов равноточных измерений (/ = 1, 2,т).

Вес результата /-го ряда равноточных измерений определяют по формуле



где пi и Sx, — объем и дисперсия /'-го ряда равноточных измерений;

С — любое, отличное от нуля число.

Обычно С выбирают таким образом, чтобы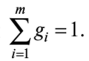 

Среднюю квадратичную погрешность результата измерений среднего взвешенного значения определяют по формуле 

Далее обработку ведут как для равноточных измерений, подставляя в формулы вместо х и S_x значения х_в и S_Xb .

Погрешности измерений

Любое измерение производится с некоторой погрешностью (ошибкой), которая искажает результат измерения и позволяет определить лишь приближенное значение измеряемой величины. Введение понятия «погрешность» требует определения и четкого разграничения понятий истинного и действительного значений измеряемой ФВ и результата измерения.

Истинное значение физической величины идеальным образом характеризует в качественном и количественном отношении соответствующую ФВ. Оно не зависит от средств нашего познания и является той абсолютной истиной, к которой мы стремимся, пытаясь выразить ее в виде числового значения. Поскольку «истинное значение» получить невозможно, то на практике его заменяют «действительным значением».

Действительное значение физической величины — это значение ФВ, полученное экспериментальным путем и настолько близкое к истинному значению, что в поставленной измерительной задаче может быть использовано вместо него.

Результат измерения ФВ — значение ФВ, полученное путем ее измерения.

Погрешность результата измерения (погрешность измерения) — отклонение результата измерения от истинного (действительного) значения измеряемой величины.

На практике при определении погрешности измерения Дх_изм используют действительное значение, в результате чего погрешность измерения определяется по формуле



где х — результат измерения;

х_д — действительное значение измеряемой величины.

Классификация погрешностей измерения по основным признакам приведена на рис. 4.8. Различные погрешности измерений в зависимости от условий измерительного процесса проявляются в различных классификационных группах. Поэтому любая классификация погрешностей измерения, в том числе и приведенная в данном пособии, является достаточно условной.

В метрологии используют понятия «погрешность измерения» и «погрешность СИ», причем погрешность СИ является одной из составляющих (часто наибольшей) погрешности измерения. Погрешности измерения и погрешности СИ по характеру проявления и способу выражения классифицируются одинаково (см. рис. 4.8).

По способу выражения погрешности делят на абсолютные, относительные и приведенные.

Абсолютную погрешность определяют как разность А = х — х_д, т.е. это погрешность измерения, выраженная в единицах измеряемой величины.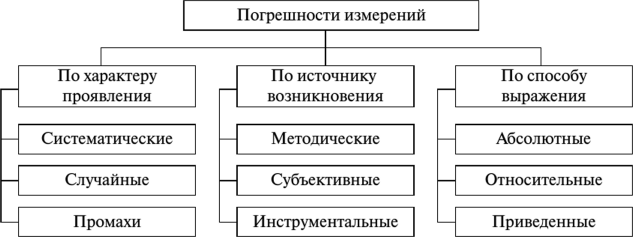



Рис. 4.8. Классификация погрешностей измерения

Абсолютная погрешность независима от измеряемой величины, поэтому она не может в полной мере служить показателем точности измерений ФВ, например, различных размеров. Например, погрешность измерения А = 0,01 мм при измерении длины Z, = 100 мм соответствует достаточно высокой точности измерений, а при L = 1 мм — низкой.

Относительную погрешность выражают отношением абсолютной погрешности измерения к действительному или истинному значению измеряемой величины.

Относительную погрешность в долях или в процентах находят соответственно из следующих отношений:



Тогда из предыдущего примера при измерении длины Z, = 100 мм, 5* = (0,01/100) • 100 = 0,01%, а, при L = 1 мм -5* = (0,01/1) • 100 = 1%.

Относительная погрешность является более информативной, так как дает возможность объективно сопоставлять результаты и оценивать качество измерений, выполненных в разное время, различными средствами или операторами, а также ранжировать погрешности измеряемой величины с различными размерностями и числовыми значениями.

Однако относительная погрешность измерения не может быть использована для нормирования погрешности некоторых СИ (например, электроизмерительных приборов), поскольку при приближении измеряемой величины к нулю незначительные ее изменения приводят к громадным изменениям 8_Х.

Исключение указанного недостатка возможно при нормировании приведенной погрешности измерения.

Приведенной называется относительная погрешность у (%), выраженная в процентах от некоторого нормирующего значения xrf.



Часто за нормирующее значение принимают верхний предел измерений СИ, т.е. x_N — x_max.

По характеру проявления погрешности измерения делятся на систематические Д_с и случайные А.

Систематическая погрешность измерения — составляющая погрешности результата измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же ФВ.

Отличительной особенностью систематических погрешностей является предсказуемость их поведения. Они могут быть почти полностью устранены путем введения соответствующих поправок. К систематическим постоянным погрешностям (остающимся постоянными при повторных измерениях) можно отнести погрешности от несоответствия действительного значения меры, с помощью которой выполняют измерения, ее номинальному значению, а также погрешности, вызванные температурной деформацией измеряемой детали или СИ при отклонении температуры от нормальной области значений. Примером систематической переменной погрешности, закономерно изменяющейся при повторных измерениях одной и той же ФВ (рис. 4.9), является, например, погрешность, вызванная износом измерительного наконечника СИ при контактных измерениях.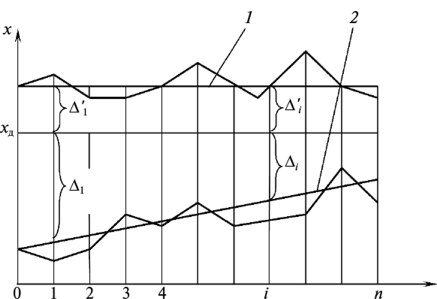



Рис. 4.9. Систематические погрешности Д_с:

1 — постоянная (Д] = Д₂ = ... = Д,- = const), 2 — переменная (Д{ * Д₂ * ... *

ф А; ф const); п — номер повторяемого измерения; Д, и Д,' — систематические погрешности /-го измерения

Случайная погрешность измерения — составляющая погрешности результата измерения, изменяющаяся случайным образом при повторных измерениях, проведенных с одинаковой тщательностью, одной и той же ФВ.

В проявлении этих погрешностей не наблюдается какой-либо закономерности, они обнаруживаются при повторных измерениях одной и той же величины в виде некоторого разброса получаемых результатов. Случайные погрешности неизбежны, неустранимы и всегда присутствуют в результате измерения. В отличие от систематических случайные погрешности нельзя исключить из результата измерения путем введения поправок, однако их можно существенно уменьшить путем увеличения числа единичных измерений. Причин, вызывающих случайные погрешности, большое количество. К ним относятся перекосы элементов прибора, нерегулярные изменения моментов трения в опорах, колебания температуры окружающей среды, округления показаний прибора, изменение внимания оператора и др.

К случайной погрешности результата измерения относится также промах, или грубая погрешность.

Промах (грубая погрешность) является результатом отдельного измерения, входящего в ряд измерений и в данных условиях резко отличающегося от остальных результатов этого ряда.

Промахи, как правило, возникают из-за ошибок или неправильных действий оператора, кратковременных резких изменений условий проведения измерений и др. Если промахи обнаруживаются в процессе измерений, то результаты, их содержащие, отбрасывают как недостоверные. Как правило, выявление промахов производится на основании анализа результатов измерений с помощью различных вероятностных критериев.

Обязательными компонентами любого измерения являются СИ, метод измерения и оператор, проводящий измерения. В связи с этим по источнику возникновения различают инструментальные, методические и субъективные погрешности.

Инструментальная погрешность измерения — это составляющая погрешности измерений, обусловленная погрешностью применяемого СИ.

Методическая погрешность измерения (погрешность метода измерения) — это составляющая систематической погрешности измерений, обусловленная несовершенством принятого метода измерений.

Она обусловлена рядом факторов: ограниченной точностью расчетных формул, положенных в основу измерений; влиянием приема использования СИ; экстраполяцией значения свойства, измеренного на ограниченной части объекта, на весь объект и др.

В большинстве случаев методические погрешности носят систематический характер, однако возможно и случайное их проявление, например, если уравнения метода измерений включают коэффициенты, зависящие от условий измерений, которые меняются случайным образом.

Субъективная погрешность измерения — часть погрешности измерения, зависящая от оператора. Она обусловлена погрешностью отсчи- тывания оператором показаний, влиянием теплоизлучения оператора на СИ и погрешностями, связанными с квалификацией оператора.

При изготовлении изделий машиностроения значительная часть проводимых измерений приходится на долю измерений геометрических параметров деталей: линейных и угловых размеров, отклонений формы и расположения поверхностей, шероховатости, параметров точности резьб, зубчатых колес и др. Поэтому рассмотрим более подробно формирование погрешностей измерения геометрических параметров деталей.

Погрешность А измерения геометрических параметров деталей с учетом условий и метода измерений можно рассчитать по зависимости [17]: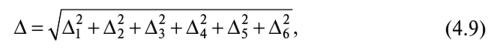



где А] — погрешность СИ;

Д₂ — погрешность метода измерений;

А₃ — погрешность от температурных деформаций;

Д₄ — погрешность от измерительного усилия;

Д₅ — субъективные погрешности оператора;

Д₆ — прочие составляющие погрешности измерений, не охваченные составляющими Aj—Д₅.

Под погрешностями Ai—Д₄ понимают предельную погрешность, включающую неисключенную систематическую и случайную составляющие. Погрешность СИ Aj: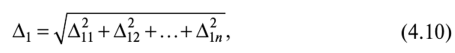



где  — основные погрешности СИ (инструментальная погрешность, погрешность установочных мер и др.), используемых в рассматриваемой измерительной установке.

Методическую погрешность измерения Д₂ можно определить по зависимости: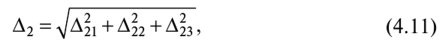 

где Д₂₁ — погрешность базирования объекта измерения;

Д₂₂ — погрешность, зависящая от процедуры измерений;

Д₂₃ — прочие составляющие погрешности метода измерений, например, погрешности, зависящие от свойств и состояния объекта измерения.

Например, при измерении диаметра детали микрометром вследствие несовершенства процедуры измерений может появиться погрешность из-за отклонений от перпендикулярности обшей оси микрометрического винта и измерительной пятки относительно оси детали. К методическим погрешностям, зависящим от процедуры измерений, относится погрешность от неполноты ощупывания измеряемой поверхности, т.е. от того, что измеряемая деталь измерена не во всех точках или сечениях.

Часто методическая погрешность определяется состоянием и свойствами объекта измерения. Например, к методическим погрешностям относятся погрешности, вызванные отклонениями формы и шероховатостью измеряемых деталей.

Погрешность Д₃, вызванная температурными деформациями,



где Д,,, Д,₂ — соответственно систематическая и случайная погрешность от температурных деформаций: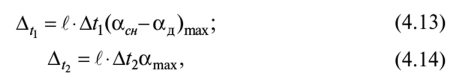



где 1 — измеряемый размер;

Д,, — допускаемое при измерении отклонение температуры среды от нормальной области значений (20 °С);

Д_?2 — допускаемое при измерении колебание температуры среды;  — максимально возможная разность коэффициентов линейного расширения элементов СИ и объекта измерения;

«шах — максимальный по величине коэффициент линейного расширения (материала элемента СИ или объекта измерения).

Погрешность от чрезмерного измерительного усилия Д₄ вызвана упругими деформациями установочных узлов СИ и деформациями в зоне контакта измерительного наконечника и измеряемой детали. Эту погрешность учитывают при высокоточных измерениях, когда допускаемые погрешности измерения соизмеримы с величиной контактных деформаций. СИ с малым измерительным усилием отличаются обычно большей случайной погрешностью измерения из-за чувствительности их к воздействию влияющих факторов, например, вибраций, так как малое измерительное усилие не обеспечивает надежного силового замыкания измерительной цепи «прибор — деталь».

Погрешности, зависящие от оператора (субъективные погрешности) Д5, подразделяют на четыре вида: погрешности отсчитывания, присутствия, действия и профессиональные погрешности. Из субъективных погрешностей поддается учету, как правило, лишь погрешность отсчитывания. Субъективная погрешность присутствия проявляется в виде влияния теплоизлучения оператора на температуру окружающей среды. К субъективным погрешностям действия относят погрешности, вносимые оператором при настройке СИ, подготовке объекта измерения и др. Профессиональные погрешности связаны с квалификацией оператора, отношением его к процессу измерения.