Монография. Оглавление ввдение. Глава I. Обзор исследований по тепло и массопереносу в пористых средах
 Скачать 284.83 Kb. Скачать 284.83 Kb.
|
|
§-3.3. Численный алгоритм ресчета неизотермической многофазной фильтрации. При правильной поставленной, хорошо смодилированной рацио-нально алгоритмизированной задаче объем информации, которые полу-чается из расчетов, значительно полнееи существенно дешевле соот-ветствующих экспрементальных исследование. Однако широкое вне-дрение численных алгоритмов для практических целей требует от них достаточной простаты в надежности. Заметим при всего, что для подовляюшего большинства задач неизотермической фильтрации на доказаны теоремы существовании и единственности решения. Само математические постановка задачи,как правило, в точном смысле не сформулировано, а дается только физическая постановка, что далеко не одно тоже. Математические трудности изучения такого типа задач связаны с нелинейностью систем уравнений, а также с большим числом независымых переменных. Математические модели разработанные в §-3.1 и §-3.2 являются даволно сложными нелинейними, что непозволяет исследовать их ана-литическими методами. Если учесть условие теплообмена с внешними покрывающими и подстилающими пласт породами, то математическая модель еше усложняется. Таким образом становится очевидным, что исследование надо проводит численными методами. Численные решение является нетолько способом получения количественных характеристик, но и методом устоновления закономерностей изучаемого процесса. Наиболе эффективным методом решения оказалась прямые прямое численное моделирование физического процесса с последующим провидением вычислительного эксперимента. В последные годы в бывщем ВЦ АН СССР проводились ряд численных экспериментов по исследованию сложных гозодинами-ческих течений с использованием нестационерного метода “крупных частиц” [34]. Впервые с помощью “крупных частиц” численное моделирование процесса неизотермической фильтрации, проведено в работах [12-14, 77-87]. Сущность метода “крупных частиц” заключается в следующем: моделирования среда заменяется сисчтемой частиц (жидких-“крупных” - частиц), которые распределе-ны в начальной момент времени по ячейком эйлеровой сетки в координатном прастранстве в соответствие с начальными данными; эволюция такой системы во времени осущес-твляется путем следующего расщепления – в начале изучается измене-ние внутренного состояния подсистем, находящихся в ячейках, в предположений их заторможенности или неподвижности, а затем рассмотривается смещение всех частиц, пропорционально их скорости и времени, без изменения внутренного состояния подсистем с послудующим пересчетом расчетной сетки в исходное состояние. Согласно методу “крупных частиц” систему уравнений (3.17)-(3.18) расщепляем по физическим процессом и в области Ω = {(x,y,z) ; 0 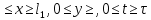 } }вводим пространственно-временную эйлеровые сетки 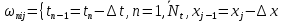 , ,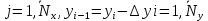 } (3.47). } (3.47).Среду моделируем системой из жидких частиц, совпадающих в данный момент времени с ячейкой эйлеровой сетки. Расчеты каждого временного шага разбиваем на три этапе: I - этап – пренебрегаем эффектами связанными с перемещениемэлементарной ячейки, аппраксимируем уравнения (3.17)-(3.18) в момент времени 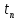 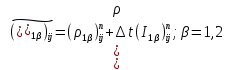 (3.48) (3.48)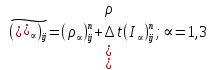 (3.49) (3.49)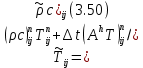 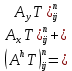 , ,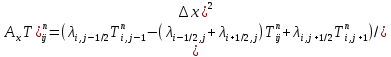 , ,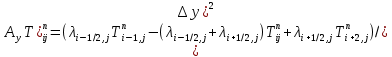 . .Численное решение эллептического уравнения (3.31) прводим с использованием методом установления и переменных направлений то есть аппракцимируем не эллептическое уравнение (3.31), а параболоическое, решение которого при независящих от времени граничных условиях при достаточно больших значениях 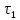 должно стремится к решению уравнения (3.31). Таким образом разностная аппраксимация уравнения (3.31) имеет вид: должно стремится к решению уравнения (3.31). Таким образом разностная аппраксимация уравнения (3.31) имеет вид: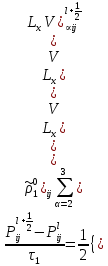 , ,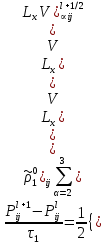 где 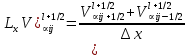 , , 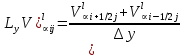 , ,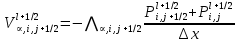 , , 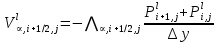 , ,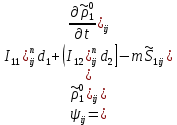 , ,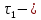 итерационный шаг, l-номер итерации, итерационный шаг, l-номер итерации,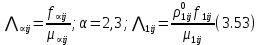 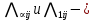 определяется по полученным на данном этапе значениям fи определяется по полученным на данном этапе значениям fи 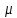 из соотношений (3.24)-(3.25). Уравнения системы (3.51-3.52) реша-ются по переменно однородной прогонкой. При неизвестных из соотношений (3.24)-(3.25). Уравнения системы (3.51-3.52) реша-ются по переменно однородной прогонкой. При неизвестных 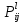 из уравнения (3.51) находятся а затем, используя значения эти значения определяются из уравнения (3.51) находятся а затем, используя значения эти значения определяются 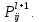 При l=0, При l=0, 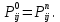 Процесса итерирования закончивается, когда невязко Процесса итерирования закончивается, когда невязко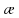 достаточно малая величина достаточно малая величина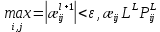 , , 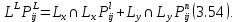 Скорость фаз вычисляются на следующим формулам: 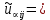 - - 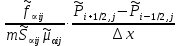 , , 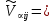 - - 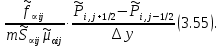 II – этап. Вычисляем перенос массы и энергия каждой фазы и компоненты через границы ячеек. Потоки величингазовой фазы вычисляется по следующим формулам: 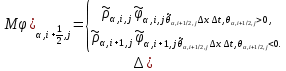 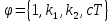 (3.56) (3.56)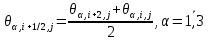 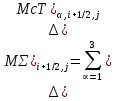 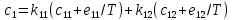 (3.57). (3.57).Потоки величин жидких фаз определяются как по приведением выше схемам, так и по схемам: 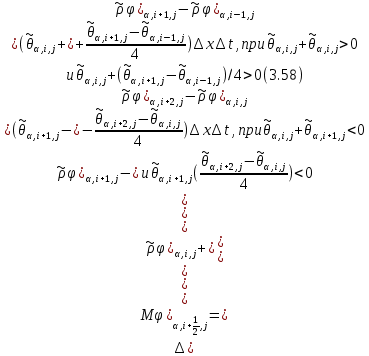 в остальных случаях 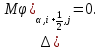 III этап. На основе законов сохранения находятся значения параметров фаз и их компонент на новом временам слое 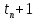 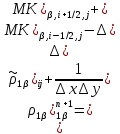 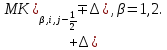 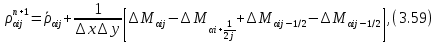 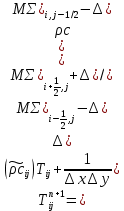 Значение 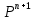 находится из (3.58) по расчетной схеме указанной на этапе 1. Значения находится из (3.58) по расчетной схеме указанной на этапе 1. Значения 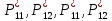 вычисляется по формулам (3.27)-(3.30) с исползованием значений параметров полученных на этом этапе. вычисляется по формулам (3.27)-(3.30) с исползованием значений параметров полученных на этом этапе.По неизвестным значениям Т, Р вычисляются скорости фазовых переходов по формулам (3.26). В алгоритме сначало призводится расчет параметров фаз, затем компонент фаз. Распределения температуры в окружающих породопределяем по схеме 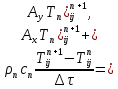 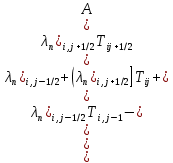 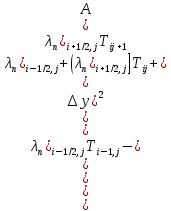 Из самого характера построения расчетной схемы следует, что здесь решается полная система нестационарных уравнений неизотер-мической фильтрации, проичем каждый вычислительный цикл предос-тавляет собой законченный процесс расчета данного временного интервала. При этом удовлетворяется все исходные нестоционарных уравнения, граничные условия задачи и определяется действительное течения жидкости в пористой среде в соответствующий момент времени. В этом численным методом расмотривается дивергентные формы исходных и разностных уравнений. Из самого характера построения расчетной схемы следует, что здесь решается полная система нестационарных уравнений неизотер-мической фильтрации, проичем каждый вычислительный цикл предос-тавляет собой законченный процесс расчета данного временного интервала. При этом удовлетворяется все исходные нестоционарных уравнения, граничные условия задачи и определяется действительное течения жидкости в пористой среде в соответствующий момент времени. В этом численным методом расмотривается дивергентные формы исходных и разностных уравнений.Из I и II этапах используется различного вида аппраксимации, что способствует устронению флюктуации и позволяет получать удовлетворителное результаты при сравнительно небольшом числе ячеек сетки. Все эти приводит к концервативным схемам, т.е. законы сохранения для всей сеточной области является здесь алгебраическим следствие разностных уравнений. |
