Монография. Оглавление ввдение. Глава I. Обзор исследований по тепло и массопереносу в пористых средах
 Скачать 284.83 Kb. Скачать 284.83 Kb.
|
|
Глава III. Численное моделирование нестоционарной неизотермической многофазной фильтрации §-3.1. Математическая модель нестоционарной неизотермической многофазной фильтрации При воздействии на нефтяные пласти голрячей водой, нагретими газами, водяным паром создаются услдовия для фазовых изменений, а также для изменение их некоторых физических и физико-химических свойств. В нефтянном пласте при этом формируется многофазный многокомпонентный поток жидкостей и газов с различной температурой. Общей теории всех процессов, призходящих в пористой среде при термическом воздействии еще нет. Отсутствие такой теории объясня-ется многими причинами, среде которых немалое значение имеют недостаточная изученность механизма фильтрации, отсутствие математической модели и эффективных численных методов. Вместе с тем в последние годы появились работы Ю.П. Желтова, А.К. Курбанова, А.В. Лыкова, В.Н. Никалаевского, М.Д. Розенберга, Р.И. Нигматулина и др., в которых развивается теория фильтрации многокомпонентных систем, в том числе и неизотермической [40,88,104-108, 119,137, 138, 149-150, 158-160]. Результаты этих работ позволяют сформули-ровать основной диффренциальные уравненгия неизотермической фильтрации при ермическом воздействии на нефтя-ные пласти. В часности, ниже такого рода уравнения будут получены из диффренциальных уравнений переноса вещества и энергии М – компонентной системы. Пологаем фильтрационные потоки N фазными, причем каждая фаза в своей очередь может состоять из М различных компонент. Обозначим приведенную плотность 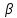 –го компонента в –го компонента в 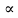 - фаза через - фаза через 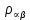 , а приведенную плотность , а приведенную плотность 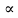 - фазы через - фазы через 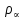 . Тогда можно записать . Тогда можно записать 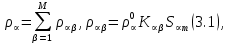 где 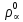 – истинная плотность фазы – истинная плотность фазы 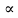 , , 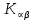 - массавоя доля - массавоя доля 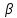 - го компонента в фазе - го компонента в фазе 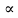 . . 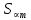 - насищенность порового пространства фазой - насищенность порового пространства фазой 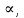 m- пористость пласта. Законы сохранение массы m- пористость пласта. Законы сохранение массы 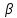 –го компонента смеси и фазы –го компонента смеси и фазы 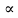 запишем в следующем виде: запишем в следующем виде: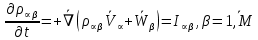 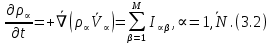 где 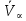 - истинная фазовая скорость, - истинная фазовая скорость, 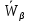 - плотность диффизионного потока, - плотность диффизионного потока, 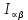 - интенсивность перехода массы из фазы - интенсивность перехода массы из фазы 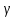 в фазу в фазу 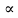 . .Фазовые скорости определим следжующим образом:  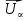 = =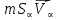 (3.3). (3.3).Фильтрационую фазовую скорость 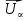 можно определить обобўеннқм законом Дарси. можно определить обобўеннқм законом Дарси.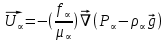 (3.4), (3.4),где 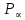 - давление в фазе - давление в фазе 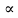 , g ускарение свободного падения, , g ускарение свободного падения, 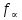 - относительная фазовая проницаемость, - относительная фазовая проницаемость, 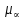 - динамическая вязкость фазы. - динамическая вязкость фазы.Закон сохранения энергия определяется на следующего диффренциального уравнения: 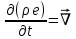 (Je) (3.5), (Je) (3.5),где Je – поток энергия в системе, e – уделная энергия системы, 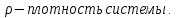 В связи тем, что в пласт вводится больше количества тепло, то некоторыми преврашениями в тепловую энергию, которые приисходить например, в результате трения фильтрирующехся жидкостей и газов, в следствии изменения объёмов газа и т.п. можно пренебречь. Эти упрашения дают возможность перейти от уравнения сохранения энергии (3.5) к уравнению сохранения энтальпии, т.е. 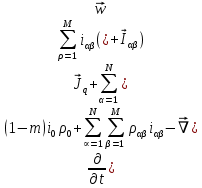 (3.6), (3.6),где 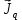 – плотность потока тепло, передаваемого путем теплопровод-ности, – плотность потока тепло, передаваемого путем теплопровод-ности, 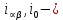 удельная энтальпия удельная энтальпия 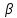 го компонента и склета порисиой среды, го компонента и склета порисиой среды, 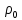 – плотность склета пористой среды. – плотность склета пористой среды.Плотность потока тепло за счет теплопроводности определяется следующим равенством: 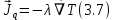 λ – эффективный коэффициент теплопроводности, характеризующий малекуль-ярный перенос тепло через склет пористого тело и содержа-щееся в нем жидкости и газа. λ 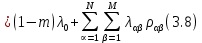 . .Если предположить, что перенос тепло за счет диффузионного движения жидкостей и газа пренебрежимо мал в сравнении с конвек-тивным переносом тепла, то уравнение (3.6) имеет вид 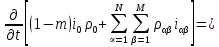 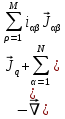 Полагая 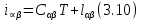 где 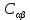 – удельная теплоеькость, – удельная теплоеькость, 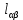 – теплота фазовых переходов, получим – теплота фазовых переходов, получим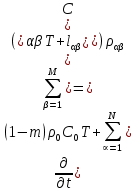 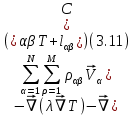 Введем обозначения 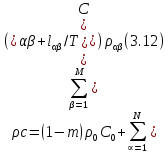 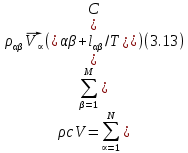 и окончательно получим 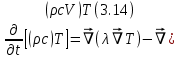 Уравнение (3.14) спреведливо и для окружающих пласт пород если учесть отсутствие в них конвективных потоков: 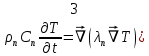 .15). .15).Система уравнений (3.2) - (3.4), (3.14), (3.15) позволяет дать коли-чественную оценку параметров тепломассапереноса в пласте и окружающих его породах при тепловом воздействии на нефтянные пласти. Однако выше уже отмечалисьтрудности реализации этой возможности. Поэтому исследователи обычно идут на значительное упрошение проблемы, делая различные допущения относительно характера теплопередачи в пласт и теплообмена с окружаюшей средой, влияния гравитационный сил и др. §-3.2. Математическая модель вытеснение нефти водяном паром. При нагнетания водяных паров по мере их продвижения в пласте пар конденсируется, а освобождающееся при конденсации тепло расхо-дуется на испарение нефти и воды в зоне пара. При этом тепло в зоне пара не расходуется на нагревание склета, так как склет в зоне пара уже нагрет до температуры нагнетаемого пара. Испаривщаясия нефт переходить в условную зону горячей воды, где она конденсируется. Вода, перехода к холодную зону, охлаждается до начальной темпера-туры пласта, а освобождающиееся при этом тепло расходуется на нагрев склета до температуры нагнетаемого пара и на теплопатерии в окружающие пласт породы. В работе [3] была попитка математического описания механизма вытиснения нефти паром. В этой работе введено в рассмотрение неиз-вестная подвижная граница, на которой температура пласта совпадает с его начальной температурой и которая подлежить определению из специально выписиваемого условия энергетического баланса. Матема-тическая модель рассмотренная в работе [3] было уточнена в работе [78], где условия теплообмена между пластом и окружающими пласт пародами учитивался по схеме «сосредоточонной емкости». Результаты расчетов показали, что учеть тепловых потерь через кравлю и подошву пласта приводит к занижению расчетной температуры, причем с ростом тепловых потерь зоны тепловые потеры увеличивается и скорост тепловых потер возрастает. Кроме того, крывые температуры стано-вится боле монотонными. При учете тепловых потерь температура паровой зоны заметно изменяется во времены. Однако здесь неучиты-валось гидродинамика пласта. Ниже будем описивать процесса более точным математическим моделем. Тепломассапереноса в пласте представит трехфазным патоком, содержащим газ, воду и нефть. Газовая фаза, в свою очеред, состоит из двух компонент: водяного пара и паров нефти. Здесь и далее 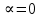 – твердая фаза, – твердая фаза, 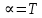 – газовая фаза, – газовая фаза, 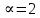 – фаза воды, – фаза воды, 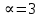 – фаза нефти и – фаза нефти и 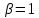 – водной пар, – водной пар, 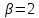 – газообразная нефть. – газообразная нефть.Тогда система уравнений (3.1)-(3.15) примет вид [13,14]: 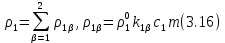 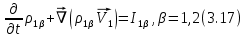 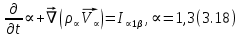 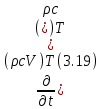 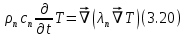 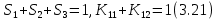 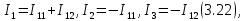 где 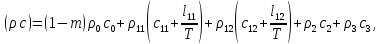 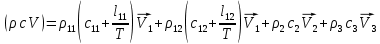 . .Сформулируем теперь замикающие соотношения для рассмо-триваемых процессов. Будем считать, что жидкости несжимаемы, а уравнение состояния газовой фазы имеет следующий вид: 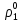 = =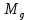 P/RTZ (3.23), P/RTZ (3.23),где 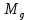 = =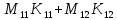 -малекулярная масса газа, -малекулярная масса газа,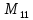 - малекулярная масса водяного пара, - малекулярная масса водяного пара,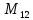 - малекулярная масса газаобразные нефти, - малекулярная масса газаобразные нефти, R – универсальная газовая постоянная, Z- коэффициент сжимаемости. Относительно газовой проницаенмости будем определять на соот-ношений: 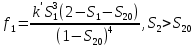 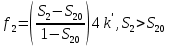 (3.24) 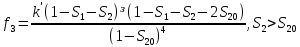 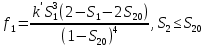 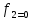 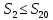 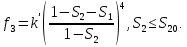 Зависимости вязкости фазот температуры представим в виде(взяты из справоч-ников по теплофизическом свойствам жидкости и газов): 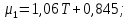 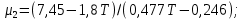 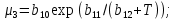 (3.25) (3.25)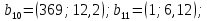 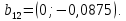 Интенсивность массовых переходов, обусловленных только испа-рением и конденсоцией воды и нефти, будем определить на следующих соотнощений 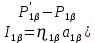 ), ), 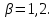 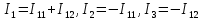 (3.26) (3.26)где 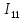 - массавоя скорость испарения воды, - массавоя скорость испарения воды,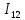 - массавоя скорость испарения нефты, - массавоя скорость испарения нефты,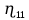 – коэффициент испарения воды, – коэффициент испарения воды,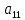 - плошадь поверхности раздела газ-вода на единицу объема, - плошадь поверхности раздела газ-вода на единицу объема,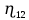 – коэффициент испарения нефты, – коэффициент испарения нефты,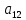 - плошадь поверхности раздела газ-нефт на единицу объема, - плошадь поверхности раздела газ-нефт на единицу объема,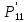 - давление насыщенных паров воды, - давление насыщенных паров воды,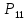 – парицальное давление паров воды в газовой фазе, – парицальное давление паров воды в газовой фазе,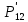 - давление насыщенных паров нефты, - давление насыщенных паров нефты,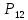 – парицальное давление паров нефты в газовой фазе. – парицальное давление паров нефты в газовой фазе.Давление насыщенных паров воды и нефти определяем но соотношений: Р – для паров воды 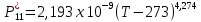 ; (3.27) ; (3.27)Р – для паров нефты(уравнение Ашворта) lg( 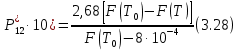 где Т- температура смеси, 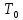 - температура кпения смеси при атмосферном давлений. - температура кпения смеси при атмосферном давлений.F(T)=( 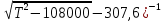 (3.29). (3.29).Считая газ смесью поров воды и нефти, а соответствие с законом Дальтона, для парисальных давлений паров воды и нефти, можно запи-сать равенство. 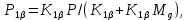 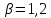 (3.30). (3.30).При предположения постоянства истенных плотностей фильтри-рующихся жидкостей и несжимаемости пористой среды, разложив производную по времени в уравнений (3.18) и просуммировов получен-ные уравнения (3.21)-(3.22) получим: 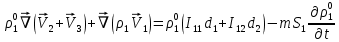 (3.31), (3.31),где 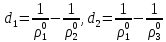 (3.32). (3.32).Из уравнение (3.31) с учетам (3.32) можно определить давление Р. На границах области фильтрации возможно задание различных усло-вии: отсутствие объемный расходов через границу, объемный расходов через границу, постоянные давление и температура на границе. Часть границы, где отсутствует объемный расход жидкостей и газов, обозна-чим через 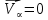 (3.33) (3.33)Это эквивалентно условию 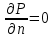 на на 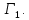 Част грвницы, где задан объемный расход 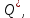 обозначим через обозначим через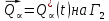 (3.34). (3.34).На границе, где известно давление, пусть это бедет 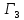 , условия имеет вид: , условия имеет вид:Р = Р( 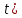 (3.35). (3.35).Кроме того должны быть поставлены граничные условия для гиперболоических уравнений переноса массы. На граница пористой среды, через которую происходит нагнетание в пласт вытисняющий жидкости или газа, задаются их количество и состав. Для парогазового воздействия на пластовую систему такое граничные условие выгладить следующим образом: 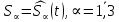 (3.36), (3.36),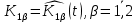 (3.37), (3.37),где 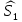 , , 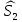 , ,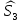 – насыщенности фаз в смеси, закачиваемой в нефтянной пласт, – насыщенности фаз в смеси, закачиваемой в нефтянной пласт, 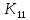 , , 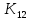 – консентрации паров воды и нефти в закачиваемой смеси. – консентрации паров воды и нефти в закачиваемой смеси.Для уравнения энергии обычно задаются следующие граничные условия. На границе 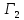 , где задан объемный расход нагнетаемых жидкостей (газов) , где задан объемный расход нагнетаемых жидкостей (газов) Т = Т 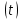 (3.38). (3.38).На границе 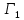 , где соответствует объемный расход жидкостей (газов) задаются законы теплообмена. В частности, если это границы пластовой системы, то задаются постоянные температура , где соответствует объемный расход жидкостей (газов) задаются законы теплообмена. В частности, если это границы пластовой системы, то задаются постоянные температураТ = Т 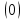 (3.39), (3.39), если это граница между продуктивном пластом и кровлей и подошвой пласта, то задаются тепловые потоки 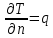 (3.40) (3.40)либо итсутствие их 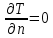 (3.41). (3.41).На границе типа 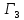 задается отсутствие теплового потока через границу задается отсутствие теплового потока через границу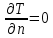 (3.42). (3.42).За начальные условия примем параметры покающиейся системы: 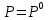 , Т = , Т =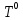 , , 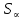 = = 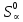 , , 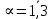 ; ; 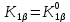 , , 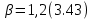 где 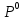 – начальное пластовое давление, – начальное пластовое давление, 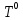 – начальное температура пласта, – начальное температура пласта, 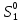 , , 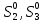 – начальные насыщенности фаз, – начальные насыщенности фаз, 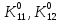 – начальные распределение концентраций паров вады и нефти в газовой фазе. – начальные распределение концентраций паров вады и нефти в газовой фазе.Прежде чем перейти к численному исследований, приведем систему уравнений (3.7)-(3.18) начальные (3.43) и граничные (3.33)-(3.42) условия к безразмерному виду. С этой цельювоспользуемся следующими записами: 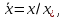 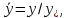 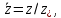 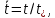 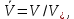 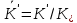 , , 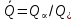 , ,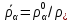 , , 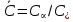 , (3.44). , (3.44).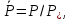 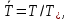 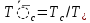 , , 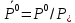 , , 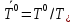 , , 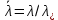 , , 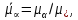 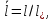 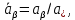 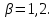 Здесь параметры со «звездочкой» обозначает некоторые посто-янные характерные величины. В качестве таковых выбираем: линейный характерный размер (расстояние между нагнетательной и эксплуа-тационной скваженами), 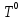 – начальная пластовая температура, – начальная пластовая температура, 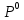 – давление на эксплуатационной скважине, – давление на эксплуатационной скважине, 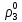 – плотность нефти в нормальных условиях, К – абсолютная проницаемость пласта, – плотность нефти в нормальных условиях, К – абсолютная проницаемость пласта, 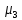 - вязкость нефти в нормальных условиях, - вязкость нефти в нормальных условиях, 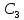 – теплоемкость нефти, после введения новых безразмерных величин (3.44) система уравнений (3.17)-(3.18), начальные и граничные условия (3.33) – (3.43) будут содержать безразмерные величины и некоторые безразмерные ком-плексы из характерных величин. Подберем еще неоределенные характерные величины – теплоемкость нефти, после введения новых безразмерных величин (3.44) система уравнений (3.17)-(3.18), начальные и граничные условия (3.33) – (3.43) будут содержать безразмерные величины и некоторые безразмерные ком-плексы из характерных величин. Подберем еще неоределенные характерные величины 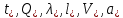 таким образом, чтобы эти комплексы равнялись единице. Тогда моделирующие уравнения как в размерном, так и в безразмерном виде будут выглядить одинакого. Отсюда таким образом, чтобы эти комплексы равнялись единице. Тогда моделирующие уравнения как в размерном, так и в безразмерном виде будут выглядить одинакого. Отсюда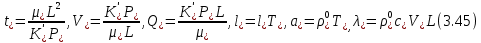 . .В неизотермических задачах вытеснения нефти, основным поко-зателям эффективности процесса является нефтоотдача. Обозначим: V – объёмные количества нефте в пласте, 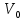 - объём нефти в пласте в началный момент времени, - объём нефти в пласте в началный момент времени, 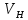 – объём нефте, остающиейся неподвижной при вытиснении. Тогда текушую нефтоотдачи пласта ɳ можно определить следуюшим образом: – объём нефте, остающиейся неподвижной при вытиснении. Тогда текушую нефтоотдачи пласта ɳ можно определить следуюшим образом:ɳ= 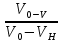 . (3.46) . (3.46) |
