|
Окружность и круг. Окружность и круг. Длина дуги. Площади круга, сектора и сегмента Цели обучения, которые достигаются на данном уроке (ссылка на учебную программу)
Раздел долгосрочного плана: 9.4 Окружность. Многоугольники
|
Школа-гимназия№1
|
Дата:05.04.2022
|
ФИО учителя: Султашева Г Д
|
Класс: 9 Г
|
Количество присутствующих:
|
отсутствующих:
|
Класс: 9 D
|
Количество присутствующих:
|
отсутствующих:
|
Тема урока
|
Окружность и круг. Длина дуги. Площади круга, сектора и сегмента
|
Цели обучения, которые достигаются на данном уроке (ссылка на учебную программу)
|
9.1.1.3 знать определение вписанного угла и его свойства
|
Цели урока
|
Учащиеся формулируют и прменяют определение свойства вписанного угла при решении задач
|
Критерии оценивания
|
Знает определение и свойства вписанного угла;
Применяет определение и свойства вписанного угла при решении задач;
Устраняет ошибки, допущенные при решении задач, если таковые имеются;
Оказывает помощь и объясняет способ решения задач;
Составляет задачи на применение свойств вписанного угла.
|
Языковые цели
|
Учащиеся будут:
- самостоятельно овладевать теоретическим материалом и применять его на практике при решении задач;
- выполнять построение чертежей;
- использовать обозначения и понятия;
- обсуждать и комментировать алгоритм решения задач и вывод формулы;
Предметная лексика и терминология:
Вписанный и ценральный углы, дуга, длина дуги (окружности), диаметр (радиус) окружности.
Серия полезных фраз для диалога/письма:
Определим вид является ли данный угол вписанный;
Угол является центральным так как …;
|
Привитие ценностей
|
Открытость и сотрудничество при парной и групповой формах работы.
При обсуждении решения проблемы, каждый учащийся может высказать своё мнение, которое будет принято остальными участниками коллектива и принято на обсуждения для определения правильности суждения, учитель акцинтирует на этом внимание.
2. Каждый учащийся, заметив ошибку или недочет может исправить её обосновав это. В этот момент другие учащиеся воспринимают критику взвешено.
3. Учитель очень внимательно слушает всех учеников, показывает им, что слышит мнение каждого из них, желательно давать обратную связь каждому ученику по его ответу.
Сотрудничество нарабатывается при использовании парной и групповой работы, во время оценивания навыков каждого ученика всем классом, при оказании помощи одноклассниками друг другу, если это разрешено учителем.
|
Ключевые навыки
|
Развитию социального навыка способствуют:
практические упражнения на взаимодействия в парах и группах;
беседы и обсуждения способов решения;
проблемная ситуация;
|
Межпредметные связи
|
Информатика – работа с мультимедийным оборудованием; работа в сети интернет по поиску информации необходимой для работы.
Физика – формула угловой скорости.
|
Навыки использования ИКТ
|
умение использовать интерактивную доску и сеть интернет для поиска необходимой информации
|
Предварительные знания
|
Окружность, элементы круга: радиус, диаметр, хорда, дуга, сектор и сегмент.
|
Ход урока
|
этапы урока
|
Запланированная деятельность на уроке
|
Ресурсы
|
Начало урока
0-3 мин
|
Организационный момент.
Учитель осматривает кабинет на готовность к уроку, проверяет наличие учащихся их готовность к получению знаний и повторяет правила поведения во время учебного занятия.
Этап создания коллаборативной среды
Положительный настрой на работу через похвалу и пожелания удачи. Мини-опрос учащихся на какие разделы и темы стоит обратить внимание на этапах повторения.
|
|
4-12 мин
|
Этап повторения ранее изученного материала.
Учащимся для самостоятельного решения предлагаются задания по ранее изученному разделу «Решение треугольников». В случае затруднения подняв руку вверх или сигнальную карточку учащийся может обозначить возникшую проблему, а учитель в свою очередь будет оказывать помощь. Работа осуществляется в тетрадях формативных работ, которые сдаются на проверку учителю для обработки результатов и дальнейшей коррекции знаний учащихся при подборе материала следующего урока или на индивидуальных консультациях.
Повторение: «Решение треугольников».
9.1.3.7 знать и применять теорему синусов;
Упражнение 1. Групповая работа с последующей взаимопроверкой.
Класс делится на несколько групп (пар) в зависимости от количества учащихся, их уровня знаний и предпочтений работы в команде. Работа организуется таким образом, что дается несколько минут на обсуждение решения внутри группы и выбора спикера, который будет представлять решение другим группам для обозрения. Ход решения может быть прописан на листе или же на ламинированной бумаге, на которой достаточно легко устранить недочеты и использовать её повторно. После обозрения хода решения каждой группой устраняются недочеты в решении, вносятся коррективы по оформлению и оценивается работа по совместно обсуждаемым дескрипторам.
|
Карточка (повторение)
|
13 мин
|
Этап постановки проблемной ситуации
Перед учащимися учитель ставит проблему, заключающуюся в том, как определить какой из углов является вписанным. На доске начерчены различные виды улов: вписанные, центральные
|
Карточка
|
14-16 мин
|
Этап оглашения темы урока, формулирования цели учебного занятия и критериев оценивания учебной деятельности учащихся.
На основании намеченных путей решения проблемы и её обсуждения совместно в процессе диалога формулируется тема учебного занятия, цель и критерии оценивания учебной деятельности на уроке как основного ориентира для достижения цели.
|
Карточка
|
Середина урока
17-37 мин
|
Этап изучения нового и материала
Учащийся А
|
Учащийся В
|
Учащийся С
|
Самостоятельно в процессе обсуждения и наводящих вопросов учителя формулируют определение и выводят свойства
|
Используя сеть интернет изучают определения и свойства
|
Используя раздаточный материал самостоятельно изучают вывод формулы
|
Деятельность учителя – Наблюдение и коррекция знаний учащихся
|
Карточка/интернет ресурс
|
Этап отработки навыка решения задач
На основании карточки и формулы предоставленной в ней учащиеся практикуются в применении формулы. Учащиеся класса делятся по уровням (А, В, С от высшего к низшему). Для каждого уровня подобраны задания, форма работы, предполагающая полное, частичное сопровождение учителя.
А и В - групповая работа(парная) – частичное сопровождение учителя; С- индивидуальная работа с частичным и полным сопровождением учителя.
Обсуждение решения заданий у доски с подробным анализом.
Пример 1. (парная работа с последующей взаимопроверкой, по образцу, представленному одним из учащихся на доске). Коррекция ошибок и определение дескрипторов оценивания работы.
Пример 2. (самостоятельная работа с последующей самопроверкой по дескрипторам, разработанным ранее).
Пример 3-4. (Совместное решение задачи у доски с полным объяснением и записью хода решения; учащиеся усвоившие материал на достаточно высоком уровне выполняют решение задачи самостоятельно и сверяются с решением, оформленным на доске и следят за отсутствием ошибок). Коррекция ошибок и определение дескрипторов оценивания работы.
Задачи для самостоятельного решения.
Деятельность учителя – Наблюдение и коррекция знаний учащихся
|
36-37 мин
|
Домашнее задание.
Рекомендации по выполнению домашней работы.
Выполнить задания по карточке и выучить необходимый теоретический материал.
|
карточка
|
38-40 мин
|
Этап подведения итогов занятия
Анализируя критерии успеха, сформулированные вначале урока учащиеся, самостоятельно подводят итог собственной работы. Учитель, акцентируя внимание на определённых моментах работы учащихся, даёт свою оценку продуктивности их деятельности, рекомендации по улучшению работоспособности.
Рефлексия. Учащиеся высказывают мнение об уровне сложности изученного материала, основных моментах, требующих закрепления. А так же оценивают свои собственные знания на конец учебного занятия.
|
|
Формы работы используемые на уроке
|
Парная работа.
Цель: развивать коммуникативный навык и учебно-организационные умения учащихся (умение объяснять, оказывать помощь, принимать помощь), через применение диалогового обучения; развивать навык взаимооценивания в соответствии с критериями оценивания; ответственность за свой результат и результат твоей команды; сплочение коллектива.
Групповая работа.
Цель: развивать коммуникативный навык и учебно-организационные умения учащихся (умение объяснять, оказывать помощь, принимать помощь), через применение диалогового обучения; развивать навык взаимооценивания в соответствии с критериями оценивания; ответственность за свой результат и результат твоей команды; сплочение коллектива.
Индивидуальная работа.
Цель: развивать навык самостоятельной работы, ответственности за свой результат, оценивания свей работы в соответствии с критериями оценивания.
ФО. Работы учащихся проводится на каждом этапе урока как учителем, так и самими учащимися в процессе самостоятельного оценивания, взаимного оценивания и обсуждения критериев и дескрипторов оценивания каждого задания.
При подведении итогов урока учитель дает обратную связь индивидуальной и обще классной работы учащихся.
Студенты в карточке отвечают на вопросы по осознанию и владению учебным материалом и настроя на роботу.
|
|
Дифференциация – каким образом Вы планируете оказать больше поддержки? Какие задачи Вы планируете поставить перед более способными учащимися?
|
Оценивание – как Вы планируете проверить уровень усвоения материала учащимися?
|
Здоровье и соблюдение техники безопасности
|
Индивидуальная, парная и групповая формы работы, направленные на развитие способностей и потребности учащихся с элементами поискового метода. Учащиеся достигшие более высокого результата усвоения учебного материала оказывают помощь другим учащимся, тем самым развивают коммуникативный навык и учебно-организационные умения учащихся (умение объяснять, оказывать помощь, принимать помощь), через применение диалогового обучения как в себе, так и других учащихся.
|
Самооценивание, взаимооценивание по результатам выполнения предлагаемых заданий; оценивание учителем индивидуального решения в тетради и у доски (пометки в тетради).
|
Здоровьесберегающие технологии, разминка в процессе взаимопроверки учащиеся пересаживаются на другие места и мини-разминка. Соблюдение правил использования интерактивной доски.
|
Рефлексия по уроку
Были ли цели урока/цели обучения реалистичными?
Все ли учащиеся достигли ЦО?
Если нет, то почему?
Правильно ли проведена дифференциация на уроке?
Выдержаны ли были временные этапы урока?
Какие отступления были от плана урока и почему?
|
Используйте данный раздел для размышлений об уроке. Ответьте на самые важные вопросы о Вашем уроке из левой колонки.
|
|
Общая оценка
Какие два аспекта урока прошли хорошо (подумайте, как о преподавании, так и об обучении)?
1:
Что могло бы способствовать улучшению урока (подумайте, как о преподавании, так и об обучении)?
1:
Что я выявил(а) за время урока о классе или достижениях/трудностях отдельных учеников, на что необходимо обратить внимание на последующих уроках?
|
Руководитель МО: __________________
|
Приложение.
Повторение: «Решение треугольников».
9.1.3.7 знать и применять теорему синусов;
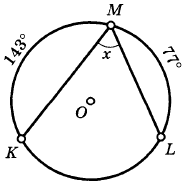
Упражнение. Найдите величины углов и сторон подобных треугольников изображенных на рисунке.
|
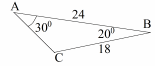 
|
9.4 Окружность. Многоугольники.
Окружность и круг. Длина дуги. Площади круга, сектора и сегмента
9.1.1.3 знать определение вписанного угла и его свойства;
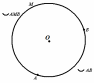
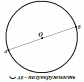
Дуга окружности
Дуга окружности – часть окружности между двумя точками окружности.
Обозначение: АВ
Дуга между концами диаметра – полуокружность.
|
|
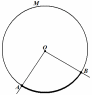
Центральный угол:
АОВ – центральный угол (вершина в центре окружности);
Градусная мера длины окружности:
АВ = АОВ (дуга меньше полуокружности),
АМВ = 360 - АОВ (дуга больше полуокружности).
Вся окружность составляет 360.
Величина полуокружности составляет 180.
|
|
Вписанный угол:
АМВ – вписанный угол (вершина лежит на окружности);
АМВ опирается на АВ.
Градусная мера вписанного угла – вписанный угол равен половине градусной меры дуги, на которую он опирается:
АМВ = 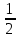 АВ = АВ = 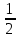 АОВ. АОВ.
|

|
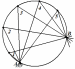
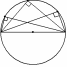
Следствие 1
Вписанные углы, опирающиеся на одну и ту же дугу, равны.
1 = 2 = 3 = 4 = 5 = …. = 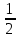 АВ. АВ.
|
|
Следствие 2
Вписанные углы, опирающиеся на полуокружность – прямые.
|
|
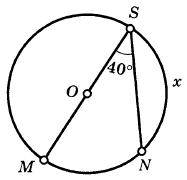
Пример 1. По данным рисунка найдите х.
|
Дано: Окр. (О; r);
MSN = 40.
|
|
Найти: SN - ?
|
Решение:
1) MSN – вписанный MN = 2MSN = 80 (по теореме о вписанном угле);
2) SM = 180 (полуокружность);
3) SM + SN + MN = 360 (эти дуги составляют окружность);
SN = 360 - SM - MN = 360 - 180 - 80 = 100.
Ответ: SN = 100.
|
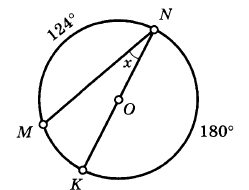
Пример 2. По данным рисунка найдите х.
|
Дано: Окр. (О; r);
MN = 124;
КN = 180.
|
|
Найти: MNK - ?
|
Решение:
1) NK + MK + MN = 360 (эти дуги составляют окружность)
MK = 360 - NK - MN = 360 - 180 - 124 = 56;
2) MNK = 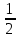 MK = 56 : 2 = 28 (по теореме о вписанном угле). MK = 56 : 2 = 28 (по теореме о вписанном угле).
Ответ: MNK = 28.
|
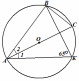
Пример 3. По данным рисунка найти ВСК.
|
Дано: Окр. (О; r);
АКВ = 65;
1 = 2.
|
|
Найти: ВСК - ?
|
Решение:
1) АКВ = АСВ = 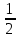 АВ = 65 (Следствие 1 из теоремы о вписанном угле); АВ = 65 (Следствие 1 из теоремы о вписанном угле);
2) АС – диаметр АКС – полуокружность АВС = 90 (Следствие 2 из теоремы о вписанном угле) АВС – прямоугольный 2 + С = 90(свойство острых углов прямоугольного треугольника), 2 = 90 - 65 = 25.
3) 2 = 1 = 25 ВАК = 50.
4) ВАК – вписанный ВАК = 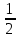 ВСК (по теореме о вписанном угле) ВСК = 100. ВСК (по теореме о вписанном угле) ВСК = 100.
Ответ: ВСК = 100.
|
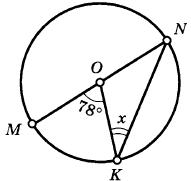
Пример 4. По данным рисунка найдите BAD и BDA, если BD = 110.
|
Дано: Окр. (О; r);
АВ – касат-я;
AD – секущая;
О AD;
BD = 110.
|
    
|
Найти: BAD, BDA - ?
|
Решение:
1) Проведём хорды ВК и BD, радиус ОВ;
2) ВКD – вписанный ВКD = 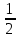 ВD = 55; ВD = 55;
3) DK – диаметр DBK = 90 (Следствие 2 из теоремы о вписанном угле) BDK + BKD = 90 (DBK – прямоугольный) BDK = 90 - 55 = 35. BDK = BDA = 35;
4) BDK – вписанный BDK = 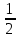 ВК ВК = 2BDK = 70 ВОК = ВК = 70 (центральный угол, опирается на ВК); ВК ВК = 2BDK = 70 ВОК = ВК = 70 (центральный угол, опирается на ВК);
5) АВ – касательная к Окр. (О; ОВ) ОВ АВ (по свойству касательной)
ОВА – прямоугольный ВОА + ВАО = 90 (свойство острых углов прямоугольного треугольника) ВАО = 90 - 70 = 20;
ВАО = BAD = 20.
Ответ: BDA = 35; BAD = 20.
|
Задачи для самостоятельного решения:
Тема: «Центральный и вписанные углы. Пропорциональность хорд и отрезков окружности»
|
|
1 вариант
|
2 вариант
|
|
1
|
Градусная мера дуги, вписанного угла, равного 520 , равна…
|
Градусная мера дуги, вписанного угла, равного 670 , равна…
|
104/134
|
2
|
Центральным углом, называется угол, образованный…
|
Вписанным углом, называется угол, образованный…
|
|
3
|
Если градусная мера дуги равна 150, центральный угол, опирающийся на неё равен…
|
Если градусная мера дуги равна 270, центральный угол, опирающийся на неё равен…
|
15/27
|
4
|
Если центральный угол равен 1680, то вписанный угол, опирающийся на ну же дугу, равен…
|
Если центральный угол равен 1360, то вписанный угол, опирающийся на ну же дугу, равен…
|
84/68
|
5
|
Один из острых углов треугольника, построенного на диаметре окружности равен 330, тогда чему равны остальные углы данного треугольника?
|
Один из острых углов треугольника, построенного на диаметре окружности равен 390, тогда чему равны остальные углы данного треугольника?
|
57,90/ 51,90
|
6
|
Окружность разбита на три части так, что градусные меры двух дуг равны, а величина третьей равна 340. Найдите величины этих дуг.
|
Окружность разбита на три части так, что градусные меры двух дуг равны, а величина третьей равна 560. Найдите величины этих дуг.
|
163,163/
152,152
|
7
|
Окружность разбита на три части так, что каждая из частей, больше другой на 7. Найдите градусные меры этих дуг.
|
Окружность разбита на три части так, что каждая из частей, больше другой на 13. Найдите градусные меры этих дуг.
|
113; 120;127
107; 120; 133
|
8
|
Окружность разбита на три части так, что два центральных угла равны 1370 и 150. Найдите величину вписанного угла, опирающегося на третью дугу окружности.
|
Окружность разбита на три части так, что два центральных угла равны 1410 и 370. Найдите величину вписанного угла, опирающегося на третью дугу окружности.
|
104/ 91
|
|

|

|
|
Домашняя работа.
 |
|
|
 Скачать 426.35 Kb.
Скачать 426.35 Kb.





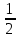 АВ =
АВ = 












