окружность. Окружность. Окружность, которая касается стороны треугольника и продолжений двух других его сторон, называется вневписанной
 Скачать 1.66 Mb. Скачать 1.66 Mb.
|
|
Пример: Найти площадь описанной равнобедренной трапеции с основаниями а и Ь. 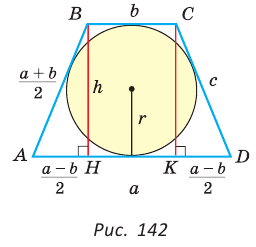 Решение: Площадь трапеции можно найти по формуле 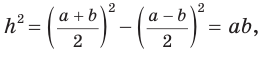 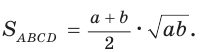 Ответ: Ответ: 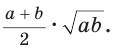 Замечание. Площадь описанной равнобедренной трапеции равна произведению среднего арифметического и среднего геометрического ее оснований. Полезно запомнить! Для описанной равнобедренной трапеции с основаниями 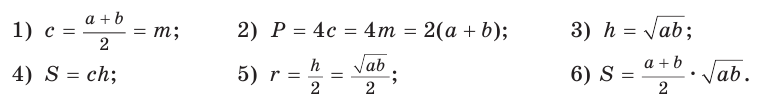 Дополнительные свойства и признаки вписанного четырехугольника Теорема. Около четырехугольника можно описать окружность тогда и только тогда, когда угол между его стороной и диагональю равен углу между противоположной стороной и другой диагональю. Рис. 143 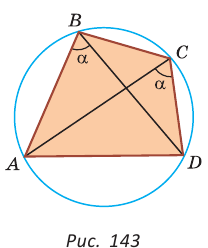 Доказательство: 1. Если четырехугольник ABCD вписан в окружность (рис. 143), то 2. Докажем, что если в некотором четырехугольнике ABCD Опишем около треугольника ABD окружность. В 8-м классе (В. В. Казаков. «Геометрия, 8», с. 186) было доказано свойство: «Геометрическим местом точек плоскости, из которых данный отрезок AD виден под углом а, является объединение двух дуг окружностей: дуги ABD и ей симметричной относительно прямой AD, исключая точки Обобщенная теорема Пифагора В прямоугольном треугольнике 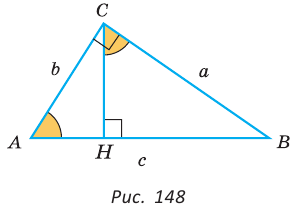 Действительно, из подобия указанных треугольников Пример: Пусть Ответ: Формула Эйлера для окружностей Для вписанной и описанной окружностей треугольника с радиусами 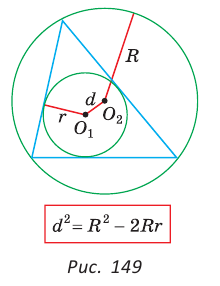 Проверим справедливость этой формулы на примере равнобедренного треугольника АВС, у которого АВ = ВС = 10, АС = 12 (рис. 150). 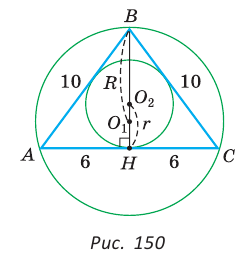 Вначале найдем расстояние между центрами указанных окружностей традиционным способом. Проведем высоту ВН, длина которой будет равна 8 (пифагорова тройка 6, 8, 10). Центры описанной и вписанной окружностей — соответственно точки 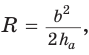 где b — боковая сторона, где b — боковая сторона, 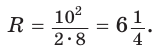 Радиус вписанной окружности Радиус вписанной окружности 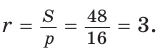 Так как Так как 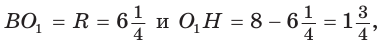 то то 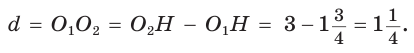 А теперь найдем d по формуле Эйлера: 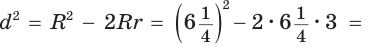 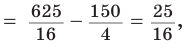 откуда откуда 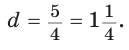 Как видим, формула Эйлера достаточно эффективна. Как видим, формула Эйлера достаточно эффективна.Запомнить: Центр описанной окружности треугольника (многоугольника) лежит в точке пересечения серединных перпендикуляров к его сторонам. Центр вписанной окружности треугольника (многоугольника) лежит в точке пересечения биссектрис его углов. Центр описанной окружности прямоугольного треугольника лежит на середине гипотенузы, а ее радиус равен половине гипотенузы: Радиус вписанной окружности прямоугольного треугольника находится по формуле 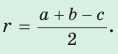 Если четырехугольник вписан в окружность, то суммы его противоположных углов равны 180°. И обратно. Если четырехугольник описан около окружности, то суммы его противоположных сторон равны между собой. И обратно. Площадь треугольника и описанного многоугольника можно найти по формуле Справочная информация по описанной и вписанной окружности треугольника Определение. Окружность называют описанной около треугольника, если она проходит через все вершины этого треугольника. 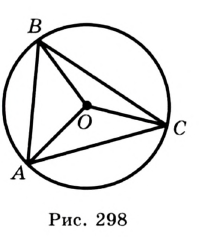 На рисунке 298 изображена окружность, описанная около треугольника. В этом случае также говорят, что треугольник вписан в окружность. Очевидно, что центр описанной окружности треугольника равноудален от всех его вершин. На рисунке 298 точка Теорема 21.1. Вокруг любого треугольника можно описать окружность. Доказательство: Для доказательства достаточно показать, что для любого треугольника 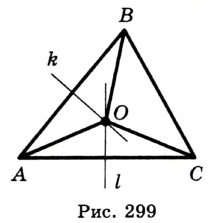 На рисунке 299 изображен произвольный треугольник Заметим, что вокруг треугольника можно описать только одну окружность. Это следует из того, что серединные перпендикуляры Следствие 1. Три серединных перпендикуляра сторон треугольника пересекаются в одной точке. Следствие 2. Центр описанной окружности треугольника — это точка пересечения серединных перпендикуляров его сторон. Определение. Окружность называют вписанной в треугольник, если она касается всех его сторон. 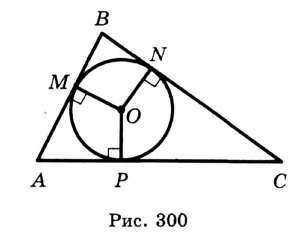 На рисунке 300 изображена окружность, вписанная в треугольник. В этом случае также говорят, что треугольник описан около окружности. Точка Теорема 21.2. В любой треугольник можно вписать окружность. Доказательство: Для доказательства достаточно показать, что для любого треугольника 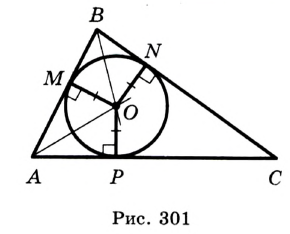 На рисунке 301 изображен произвольный треугольник Заметим, что в треугольник можно вписать только одну окружность. Это следует из того, что биссектрисы углов Следствие 1. Биссектрисы углов треугольника пересекаются в одной точке. Следствие 2. Центр вписанной окружности треугольника — это точка пересечения его биссектрис. Пример: Докажите, что радиус окружности, вписанной в прямоугольный треугольник, определяется по формуле 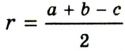 , где — радиус вписанной окружности, , где — радиус вписанной окружности, 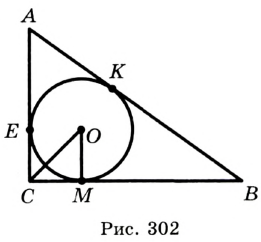 Решение: В треугольнике Отрезок Так как точка 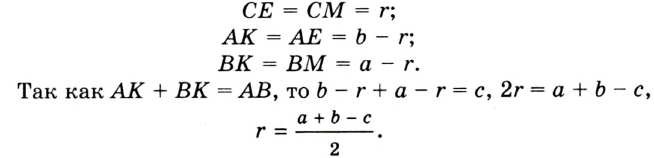 |
