окружность. Окружность. Окружность, которая касается стороны треугольника и продолжений двух других его сторон, называется вневписанной
 Скачать 1.66 Mb. Скачать 1.66 Mb.
|
|
Теорема (свойство вписанного четырехугольника). Сумма противоположных углов четырехугольника, вписанного в окружность, равна 180°. 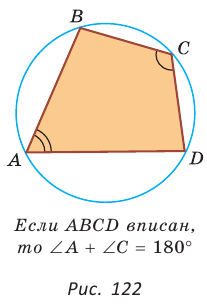 Доказательство: Пусть ABCD — четырехугольник, вписанный в окружность (рис. 122). Его углы А, В, С и D являются вписанными в окружность. Так как вписанный угол равен половине дуги, на которую он опирается, то Теорема (признак вписанного четырехугольника). Если сумма противоположных углов четырехугольника равна 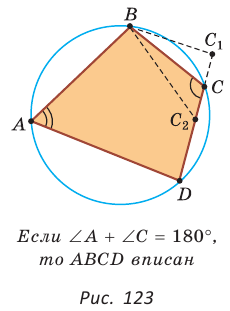 Доказательство: Рассмотрим четырехугольник ABCD, у которого Тогда сумма Замечание. Так как сумма углов четырехугольника равна 360°, то для того чтобы около четырехугольника можно было описать окружность, достаточно, чтобы сумма любой пары его противоположных углов была равна 180°. Следствия. 1. Около параллелограмма можно описать окружность, только если этот параллелограмм — прямоугольник (рис. 124, а). Центр этой окружности лежит в точке пересечения диагоналей прямоугольника. 2. Около ромба можно описать окружность, только если этот ромб — квадрат (рис. 124, б). 3. Около трапеции можно описать окружность, только если она равнобедренная (рис. 124, в). 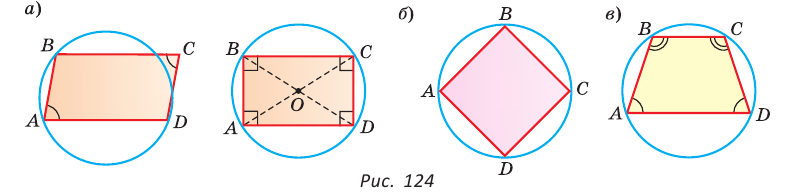 Докажите эти следствия самостоятельно. Теорема (свойство описанного четырехугольника ). Суммы противоположных сторон описанного четырехугольника равны между собой. 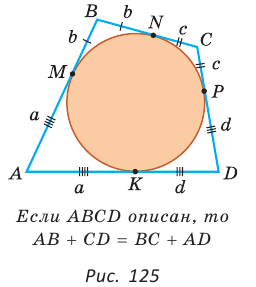 Доказательство: Пусть ABCD — описанный четырехугольник, М, N, Р и К — точки касания его сторон с окружностью (рис. 125). Так как отрезки касательных, проведенных к окружности из одной точки, равны между собой, то AM = АК = а, ВМ = BN = b, СР = CN = с, DP = DK = d. Тогда 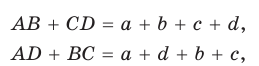 откуда AD + ВС = AB + CD. Теорема доказана. Следствие: Периметр описанного четырехугольника равен удвоенной сумме длин любой пары его противоположных сторон: Теорема (признак описанного четырехугольника). Если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность. 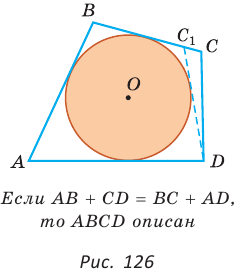 Доказательство: Пусть для выпуклого четырехугольника ABCD справедливо, что Проведем окружность, которая касается прямых AD, АВ и ВС (рис. 126). Такая окружность существует, ее центр находится в точке пересечения биссектрис углов А и В. Если окружность не касается стороны CD, то либо прямая CD не имеет с окружностью общих точек, либо является секущей. Рассмотрим первый случай. Проведем отрезок Отняв почленно от равенства (1) равенство (2), получим Рассмотрев случай, когда прямая DC — секущая, также придем к противоречию (сделайте это самостоятельно). Следовательно, данная окружность касается стороны CD и в четырехугольник ABCD можно вписать окружность. Теорема доказана. Следствия. 1. В параллелограмм можно вписать окружность, только если этот параллелограмм — ромб. Центр этой окружности лежит в точке пересечения диагоналей ромба, а ее диаметр равен высоте ромба (рис. 127, а). 2. В прямоугольник можно вписать окружность, только если этот прямоугольник — квадрат (рис. 127, б). 3. Диаметр окружности, вписанной в трапецию, равен ее высоте (рис. 127, в). Докажите эти следствия самостоятельно. 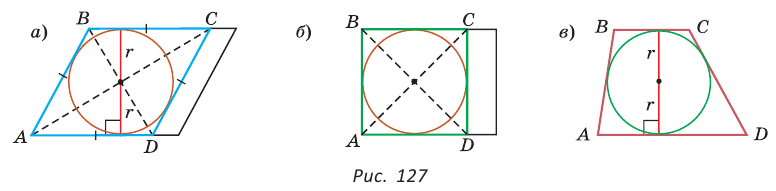 Для описанного многоугольника справедлива формула 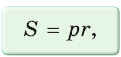 , где S — его площадь, р — полупериметр, — радиус вписанной окружности. , где S — его площадь, р — полупериметр, — радиус вписанной окружности.Доказательство аналогично приведенному в § 8 для треугольника. Выполните его самостоятельно, используя рисунок 128. 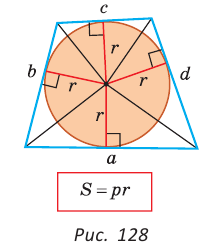 Пример: Найти радиус окружности, вписанной в ромб с периметром 24 см и острым углом, равным 45°. 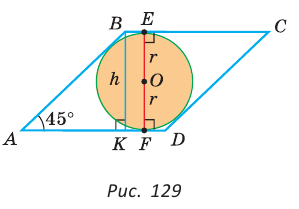 Решение: Способ 1 (решение прямоугольного треугольника). Пусть ABCD — ромб (рис. 129), О — центр вписанной в ромб окружности. Известно, что высота ВК ромба равна диаметру EF вписанной окружности, т. е. Из прямоугольного треугольника АВК находим. что 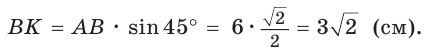 Искомый радиус вписанной окружности Искомый радиус вписанной окружности Способ 2 (метод площадей). Ромб — параллелограмм. По формуле площади параллелограмма 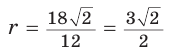 (см). (см).Ответ: Пример: Окружность, вписанная в прямоугольную трапецию ABCD, где 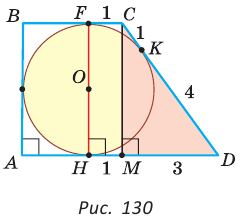 Решение: Способ 1. Площадь трапеции находится по формуле 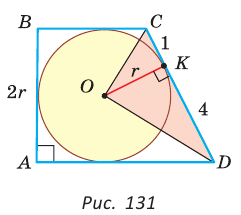 Способ 2*. Центр О вписанной окружности лежит на пересечении биссектрис углов Ответ: 18. Замечание. Полезно запомнить свойство: «Боковая сторона описанной трапеции видна из центра вписанной окружности под углом 90°». Пример: Внутри острого угла А взята точка М, из которой опущены перпендикуляры МВ и МС на стороны угла А, 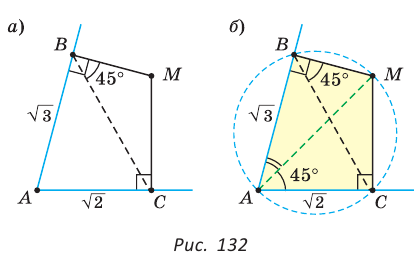 Решение: Так как в четырехугольнике АВМС сумма углов В и С равна 180°, то около него можно описать окружность. Проведем в ней хорду AM (рис. 132, б). Поскольку 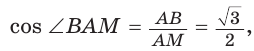 откуда откуда Ответ: 75°. Окружность, вписанная в треугольник Пример: Окружность вписана в треугольник АВС со сторонами ВС = а, АС = Ь, АВ = с. Вывести формулу для нахождения длин отрезков, на которые точки касания окружности со сторонами делят каждую сторону треугольника. 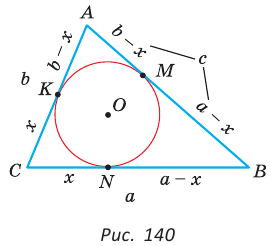 Решение: Пусть К, М и N — точки касания вписанной окружности соответственно со сторонами АС, АВ и ВС треугольника АВС (рис. 140). Известно, что отрезки касательных, проведенных из одной точки к окружности, равны между собой. Тогда, если 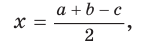 т. е. т. е. 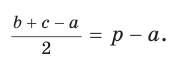 Ответ: 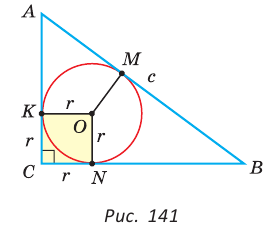 Замечание. Если Описанная трапеция |
