окружность. Окружность. Окружность, которая касается стороны треугольника и продолжений двух других его сторон, называется вневписанной
 Скачать 1.66 Mb. Скачать 1.66 Mb.
|
|
Пример: Дан равносторонний треугольник со стороной а. Найти радиус R его описанной окружности и радиус его вписанной окружности. 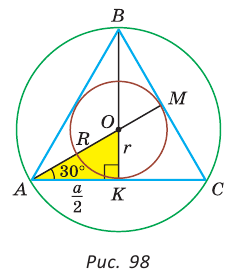 Решение: Способ 1 (тригонометрический метод).Так как в равностороннем треугольнике биссектрисы являются и высотами, и медианами, то его биссектрисы лежат на серединных перпендикулярах к сторонам треугольника. Поэтому в равностороннем треугольнике центры описанной и вписанной окружностей совпадают. Рассмотрим равносторонний треугольник АВС со стороной а, у которого высоты AM и ВК пересекаются в точке О — центре описанной и вписанной окружностей (рис. 98). Тогда ОА = OB = R — радиусы описанной, 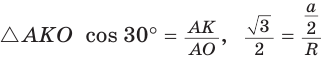 , откуда , откуда 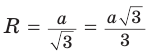 . .В 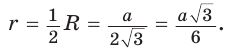 Способ 2 (свойство медиан). Поскольку AM и ВК — медианы треугольника АВС (см. рис. 98), то по свойству медиан 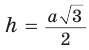 . Откуда . ОткудаОтвет: 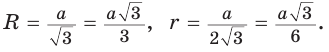 Полезно запомнить! Поскольку радиус описанной окружности равностороннего треугольника 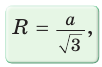 то то 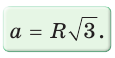 Значит, сторона равностороннего Значит, сторона равностороннеготреугольника в Чтобы найти радиус R описанной окружности равностороннего треугольника, нужно сторону разделить на 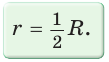 Прямоугольный треугольник и его описанная и вписанная окружности Теорема. Центр окружности, описанной около прямоугольного треугольника, лежит на середине гипотенузы, а ее радиус равен половине гипотенузы, т. е. 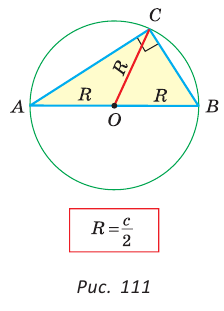 Доказательство: Проведем в прямоугольном треугольнике АВС медиану СО к гипотенузе АВ (рис. 111). Так как медиана прямоугольного треугольника, проведенная к гипотенузе, равна половине гипотенузы, то ОС = ОА = ОВ. Тогда середина гипотенузы — точка О — равноудалена от точек А, В и С и поэтому является центром описанной окружности треугольника АВС. Радиус этой окружности Теорема доказана. Замечание. Также можно доказать, что серединные перпендикуляры к катетам прямоугольного треугольника пересекаются на середине гипотенузы. Отметим, что у остроугольного треугольника центр описанной окружности лежит внутри треугольника (рис. 112, а), у тупоугольного — вне треугольника (рис. 112, б), у прямоугольного — на середине гипотенузы (рис. 112, в). Обоснуйте первые два утверждения самостоятельно. 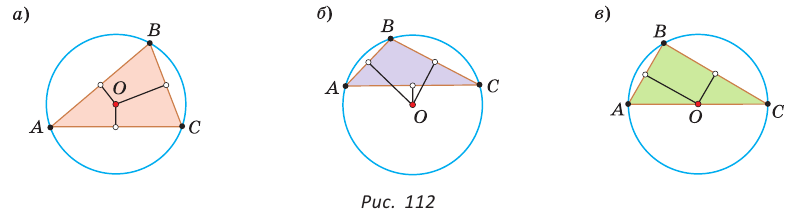 Теорема. Радиус окружности, вписанной в прямоугольный треугольник, можно найти по формуле 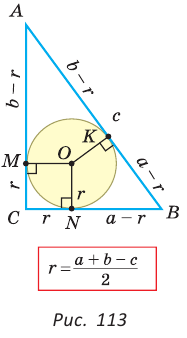 Доказательство: Рассмотрим прямоугольный треугольник АВС с катетами Проведем радиусы в точки касания и получим: Теорема доказана. Следствие: Доказательство: Преобразуем формулу радиуса вписанной окружности: 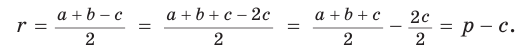 Формула 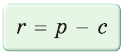 в сочетании с формулами в сочетании с формулами 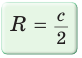 дает возможность решать многие задачи, связанные с прямоугольным треугольником, алгебраическим методом. дает возможность решать многие задачи, связанные с прямоугольным треугольником, алгебраическим методом.Пример. Дан прямоугольный треугольник, Решение: Так как 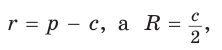 то то Из формулы Ответ: = 2. Пример: Найти радиус окружности, описанной около прямоугольного треугольника, у которого один из катетов равен 6, а радиус вписанной окружности равен 2. 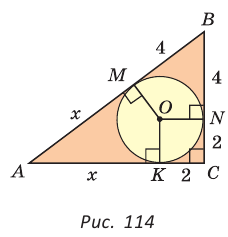 Решение: Способ 1 (геометрический). Пусть в треугольнике АВС, где По свойству касательных Тогда Следовательно, Радиус описанной окружности 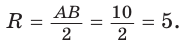 Способ 2 (алгебраический). Подставив в формулу Ответ: 5. Пример: Гипотенуза прямоугольного треугольника Решение: Способ 1 (геометрический). Пусть в 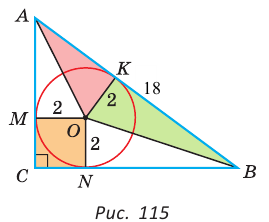 Отсюда Площадь Способ 2 (алгебраический). Из формулы 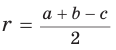 следует следует 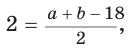 Способ 3 (алгебраический). Из формулы Ответ: 40. Реальная геометрия: Есть два листа ДСП (древесно-стружечной плиты). Один из них имеет форму равностороннего треугольника со стороной 1 м, другой — форму прямоугольного равнобедренного треугольника с катетами, равными 1 м (рис. 120). Из каждого листа необходимо вырезать по одному кругу наибольшего диаметра. Определите, из какого листа будет вырезан круг большего диаметра и каким в этом случае будет процент отходов, если известно, что площадь круга можно найти по формуле  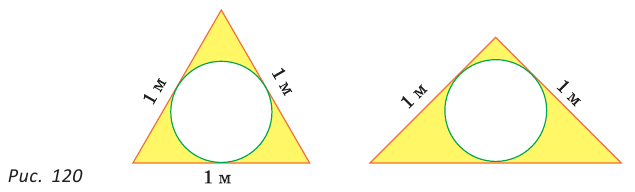 Вписанные и описанные четырехугольники Определение. Окружность называется описанной около многоугольника, если она проходит через все его вершины. При этом многоугольник называется вписанным в окружность. Окружность называется вписанной в многоугольник, если она касается всех его сторон. При этом много угольник называется описанным около окружности. Пятиугольник ABCDE (рис. 121, а) является вписанным в окружность а четырехугольник MNPK (рис. 121, б) — описанным около окружности. 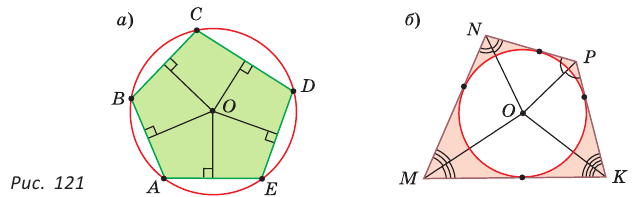 Центр описанной окружности многоугольника находится в точке пересечения серединных перпендикуляров к его сторонам, а центр вписанной — в точке пересечения биссектрис его углов. Обоснуйте эти утверждения самостоятельно. |
