Билет № 1
|
1. Определение многоугольника. Вершины, стороны, диагонали и периметр многоугольника. Формула суммы углов выпуклого многоугольника
2.  Радиус OB окружности с центром в точке O пересекает хорду AC в точке D и перпендикулярен ей. Найдите длину хорды AC, если BD = 1 см, а радиус окружности равен 5 см. Радиус OB окружности с центром в точке O пересекает хорду AC в точке D и перпендикулярен ей. Найдите длину хорды AC, если BD = 1 см, а радиус окружности равен 5 см.
3. Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AB=66, AC=44, MN=24. Найдите AM.
4. Отрезки AB и CD являются хордами окружности. Найдите длину
хорды CD , если AB = 24, а расстояния от центра окружности до хорд AB
и CD равны соответственно 16 и 12.
|
Билет № 2
|
1.Определение, признаки и свойства параллелограмма. Формулы площади параллелограмма
2.  Центральный угол AOB опирается на хорду AB длиной 6. При этом угол OAB равен 60°. Найдите радиус окружности. Центральный угол AOB опирается на хорду AB длиной 6. При этом угол OAB равен 60°. Найдите радиус окружности.
3. Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN и CM пересекаются в точке O, AN=15, CM=12 . Найдите ON.
4. Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B . Найдите диаметр окружности, если AB = 3, AC = 5.
|
Билет № 3
|
1.Определение, признаки и свойства прямоугольника, формулы площади прямоугольника
2.  Длина хорды окружности равна 72, а расстояние от центра окружности до этой хорды равно 27. Найдите диаметр окружности. Длина хорды окружности равна 72, а расстояние от центра окружности до этой хорды равно 27. Найдите диаметр окружности.
3. На гипотенузу AB прямоугольного треугольника ABC опущена высота CH, AH=3, BH=27. Найдите CH.
4. Основания BC и AD трапеции ABCD равны соответственно 6 и 24,
BD = 12. Докажите, что треугольники CBD и BDA подобны.
|
Билет № 4
|
1.Определение, признаки и свойства ромба, формулы площади ромба
2.
 В окружности с центром в точке О проведены диаметры AD и BC, угол OCD равен 30°. Найдите величину угла OAB. В окружности с центром в точке О проведены диаметры AD и BC, угол OCD равен 30°. Найдите величину угла OAB.
3. В треугольнике АВС углы А и С равны 40° и 60° соответственно. Найдите угол между высотой ВН и биссектрисой BD
4. Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 12, а одна из диагоналей ромба равна 48. Найдите углы ромба .
|
Билет № 5
|
1.Определение трапеции. Виды трапеций. Свойства прямоугольной и равнобедренной трапеций. Площадь трапеции.
2. 
Найдите ∠DEF, если градусные меры дуг DE и EF равны 150° и 68° соответственно.
3. У треугольника со сторонами 15 и 5 проведены высоты к этим сторонам. Высота, проведённая к первой стороне, равна 1. Чему равна высота, проведённая ко второй стороне?
4. В выпуклом четырёхугольнике ABCD углы DAC и DBC равны . Докажите , что углы CDB и CAB также равны
|
Билет № 6
|
1. Определение подобных треугольников. Признаки подобия треугольников. Теорема Фалеса. Применение т Фалеса для деления отрезка на n равных частей
2. 
Прямоугольный треугольник с катетами 5 см и 12 см вписан в окружность. Чему равен радиус этой окружности?
3. Боковая сторона равнобедренного треугольника равна 25, а основание равно 48. Найдите площадь этого треугольника.
4. Точка H является основанием высоты , проведённой из вершины прямого угла B треугольника ABC к гипотенузе AC . Найдите AB , если AH = 5, AC = 45.
|
Билет № 7
|
1.Синус, косинус и тангенс острого угла прямоугольного треугольника. Значение синуса, косинуса и тангенса углов 30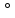 ,45 ,45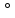 ,60 ,60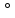 . .
2. 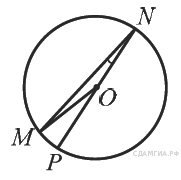 Найдите градусную меру ∠MON, если известно, NP — диаметр, а градусная мера ∠MNP равна 18°. Найдите градусную меру ∠MON, если известно, NP — диаметр, а градусная мера ∠MNP равна 18°.
3. Периметр равнобедренного треугольника равен 144, а основание – 64. Найдите площадь треугольника.
4. Через точку O пересечения диагоналей параллелограмма ABCD проведена прямая , пересекающая стороны AB и CD в точках E и F соответственно. Докажите , что отрезки AE и CF равны .
|
Билет № 8
|
1. Определение секущей и касательной к окружности. свойство отрезков касательных, проведенных к окружности из одной точки. Свойство хорд.
2. 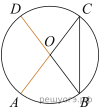
В окружности с центром O AC и BD — диаметры. Угол ACB равен 26°. Найдите угол AOD. Ответ дайте в градусах.
3.В треугольнике ABC отмечены середины M и N сторон BC и AC соответственно. Площадь треугольника CNM равна 42. Найдите площадь четырёхугольника ABMN.
4. Окружность пересекает стороны AB и AC треугольника ABC в точках K и P соответственно и проходит через вершины B и C. Найдите длину отрезка KP , если AP = 30, а сторона BC в 1,2 раза меньше стороны AB .
|
Билет № 9
|
1. Определение и свойство средней линии треугольника. Определение и свойство средней линии трапеции.
2. 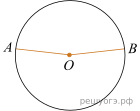
Точки A и B делят окружность на две дуги, длины которых относятся как 9:11. Найдите величину центрального угла, опирающегося на меньшую из дуг. Ответ дайте в градусах.
3. Найдите острый угол параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 33°. Ответ дайте в градусах.
4. Окружности с центрами в точках M и N пересекаются в точках S и T, причём точки M и N лежат по одну сторону от прямой ST . Докажите , что прямые MN и ST перпендикулярны.
|
Билет № 10
|
1. Определение вписанного и центрального углов окружности. Свойства вписанного и центральных углов.
2. 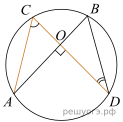
Точки A, B, C и D лежат на одной окружности так, что хорды AB и СD взаимно перпендикулярны, а ∠BDC = 25°. Найдите величину угла ACD.
3. Площадь параллелограмма ABCD равна 68. Точка E – середина стороны AB. Найдите площадь треугольника CBE.
4. Прямая, параллельная основаниям трапеции ABCD , пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF , если AD = 50, BC= 30, CF : DF= 7:3
|
Билет № 11
|
1.Теорема Пифагора. Теорема, обратная теореме Пифагора. Пропорциональные отрезки в прямоугольном треугольнике
2. 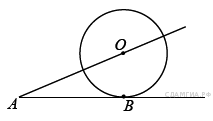 К окружности с центром в точке О проведены касательная AB и секущая AO. Найдите радиус окружности, если AB = 12 см, AO = 13 см. К окружности с центром в точке О проведены касательная AB и секущая AO. Найдите радиус окружности, если AB = 12 см, AO = 13 см.
3. В трапецию вписана окружность, боковые стороны равны 10 и 12. Найти среднюю линию трапеции.
4. В треугольнике ABC с тупым углом BAC проведены высоты BB1 и
CC1 .Докажите, что треугольники AB1C1 и ABC подобны.
|
Билет № 12
|
1.Определение площади. Свойство площади. Все формулы площади треугольника.
2. 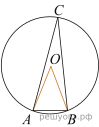
Треугольник ABC вписан в окружность с центром в точке O. Найдите градусную меру угла C треугольника ABC, если угол AOB равен 48°.
3. Сторона ромба равна 9, а расстояние от точки пересечения диагоналей ромба до неё равно 1. Найдите площадь ромба.
4. Катет и гипотенуза прямоугольного треугольника равны 18 и 30. Найдите: а) площадь; б) высоту, проведенную к гипотенузе; в) радиус окружности, описанной около этого треугольника, г) медиану, проведенную к гипотенузе, д) радиус окружности, вписанной в треугольник.
|
Билет № 13
|
1. Определение окружности, описанной около многоугольника. Многоугольник, вписанный в окружность. Свойства четырехугольника, вписанного в окружность.
2. 
Найдите величину (в градусах) вписанного угла α, опирающегося на хорду AB, равную радиусу окружности.
3. В равностороннем треугольнике ABC медианы BK и AM пересекаются в точке O. Найдите 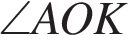 . .
4. Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите AC, если диаметр окружности равен 7,5, а AB = 2.
|
Билет № 14
|
1. Окружность, вписанная в треугольник. Окружность, описанная около треугольника. Нахождение центров этих окружностей. Рассмотреть все виды треугольников
2. 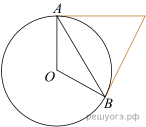
Касательные в точках A и B к окружности с центром O пересекаются под углом 72°. Найдите угол ABO. Ответ дайте в градусах.
3. В равнобедренной трапеции основания равны 4 и 8, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции.
4. Основания равнобедренной трапеции равны 8 и 18, а периметр равен 56. Найдите площадь трапеции
|
Билет № 15
|
1. Определение окружности, вписанной в многоугольник. Многоугольник, описанный около окружности. Свойство описанного четырехугольника.
2. 
В треугольнике ABC угол C равен 90°, AC = 30 , BC = 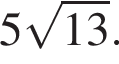 Найдите радиус окружности, описанной около этого треугольника. Найдите радиус окружности, описанной около этого треугольника.
3. В прямоугольном треугольнике один из катетов равен 10, а угол, лежащий напротив него, равен 45°. Найдите площадь треугольника.
4. Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC = 19, а расстояние от точки K до стороны AB равно 7.
| |
 Скачать 115.79 Kb.
Скачать 115.79 Kb.