лабораторная работа относительный покой жидкости во вращающемся сосуде. лр 2. Описание установки
 Скачать 475.21 Kb.
|
 Цель работы: изучить относительный покой жидкости во вращающемся сосуде путем экспериментального нахождения координат точек кривой свободной поверхности жидкости.Описание установки: 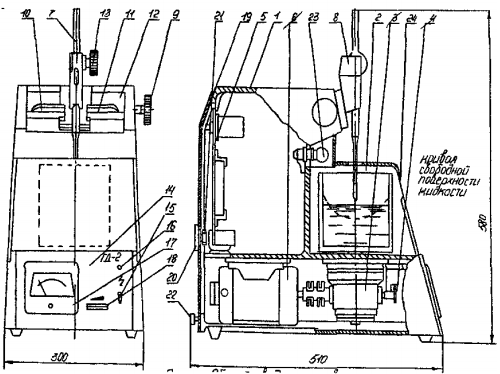 Рисунок 1 – Общий вид установки Установка содержит литой корпус 1, сосуд 2 с трансформаторным маслом, червячный редуктор 3, фотодатчик 1, блок питания 5, устройство для измерения ординат кривой свободной поверхности жидкости и электропривод с элементами управления частотой вращения. Схема кинематической установки представлена на рисунке 2. Цилиндрический сосуд заполнен на 0,6 своей высоты трансформаторным маслом и приводится во вращение электродвигателем 6 через червячный редуктор. При равномерном вращении сосуда вокруг вертикальной оси свободная поверхность жидкости в сосуде принимает форму параболоида вращения. Работа на установке заключается в экспериментальном измерении координат точек кривой свободной поверхности жидкости в диаметральной плоскости сосуда с последующим сопоставлением их с величинами координат, найденными из теоретических зависимостей. Для измерения вышеуказанных координат предназначено измерительное устройство, содержащее измерительную иглу 7 и каретку 8. При вращении рукоятки 9, каретка, а, следовательно, и измерительная игла, перемещаются в горизонтальном направлении. Отсчет перемещений (в правую или левую сторону) регистрируется по шкалам 10, 11, размещенным на направляющей 12. 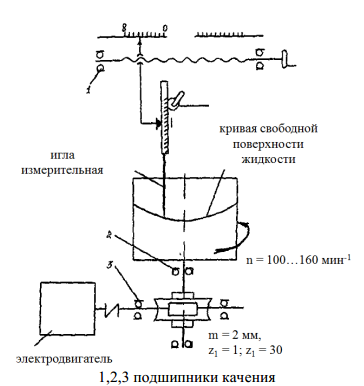 Рисунок 2 – Схема кинематическая При измерении ординат левой ветви параболы отсчет горизонтальных перемещений производят по шкале 11, а при измерении ординат правой ветви параболы – по шкале 10. Вертикальное перемещение измерительной иглы осуществляется при вращении рукоятки 13. На поверхности штока измерительной иглы нанесена шкала, по которой регистрируют вертикальные координаты свободной поверхности жидкости. Точность отсчета вертикальных перемещений не менее 0,5 мм. Для расширения методических возможностей конструкция установки предусматривает регулирование частоты вращения сосуда с жидкостью в пределах 40...160 об/мин и, как следствие, получение семейства параболических кривых свободной поверхности жидкости. Принцип измерения частоты вращения сосуда основан на измерении среднего значения импульсов тока, период следования которых пропорционален частоте вращения. Выполнение работы Лабораторная работа имеет своей целью экспериментальное измерение координат точек кривой свободной поверхности жидкости в диаметральной плоскости сосуда с последующим сравнением их с величинами координат, определенными при теоретическом расчете. В работе рассматривается случай, когда на жидкость, кроме объемных сил тяжести, действует еще система центробежных сил инерции. Пусть цилиндрический сосуд, заполненный до определенного уровня жидкостью, вращается равномерно вокруг своей вертикальной оси. Благодаря силам трения стенки вращающегося сосуда будут увлекать за собой жидкость, и через некоторое время вся жидкость начнет вращаться вместе с сосудом с той же угловой скоростью, находясь в покое по отношению к стенкам сосуда. Для исследования относительного покоя жидкости применяют уравнение равновесия (уравнение Эйлера). В данном случае объемная сила, входящая в эти уравнения, будет слагаться из силы тяжести и центробежной силы, которая направлена перпендикулярно оси вращения. Теоретические исследования показывают, что в случае кругло-цилиндрического сосуда, равномерно вращающегося вокруг своей вертикальной оси, свободная поверхность жидкости, находящейся в этом сосуде получает вид параболоида вращения с вертикальной осью, совпадающая с осью сосуда. Имея это в виду, можно утверждать, что линия пересечения искомой свободной поверхности с вертикальной плоскостью, проведенной по оси сосуда, т.е. кривая свободной поверхности жидкости является параболой с вертикальной осью. Отметки точек указанной параболической свободной поверхности относительно горизонтальной плоскости, проходящей через низшую точку свободной поверхности, находят по теоретической зависимости, полученной из уравнения Эйлера. 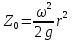 где r – кратчайшее расстояние от данной точки свободной поверхности до оси вращения, м; ω – угловая скорость, рад/с; g – ускорение силы тяжести (g =9,81 м/с). В лабораторной работе необходимо экспериментально определить отметки Z0 и горизонтальные координаты r точек кривой свободной поверхности жидкости, вращающееся вместе с сосудом, осуществляемое в процессе опытов, причем, только для одной (левой или правой) ветви параболы. При установлении искомой кривой свободной поверхности жидкости поворотом тумблера на передней панели включают электродвигатель, который приводит во вращение сосуд. Затем вращением регулятора, расположенного также на передней панели, устанавливается заданная частота вращения сосуда. Величину установленной частоты вращения можно наблюдать по стрелочному индикатору. После того, как жидкость в сосуде придет в состояние относительного покоя (по отношению к стенкам вращающегося сосуда), производят соответствующие измерения с помощью измерительной иглы. Для этого вращением рукоятки измерительную иглу устанавливают сначала в такое положение, чтобы ось ее совпадала с осью сосуда (отметка "0" по горизонтальной шкале). Затем вращением рукоятки, расположенной на каретке, измерительную иглу опускают до соприкосновения ее острия со свободной поверхностью жидкости и производят отсчет по нониусу. После этого иглу поднимают вверх и перемещают в горизонтальном направлении (влево или вправо от оси сосуда) на 1 см и снова опускают до соприкосновения ее острия со свободной поверхностью. В новом положении берут отсчеты по нониусу. Аналогичные измерения производят для ряда других точек, расположенных вдоль радиуса сосуда (7 – 8 точек). Результаты измерений записывают в горизонтальные графы таблицы отчета по работе. Затем вращением регулятора установить другую частоту вращения сосуда и повторить опыт. Таблица 1
Обработка результатов эксперимента При обработке опытных данных, записанных в таблице 1, составляют таблицу 2. Вычисляют отметку Z0опыт. точки свободной поверхности относительно горизонтальной плоскости, проходящей через низшую точку свободной поверхности, как разность отсчетов по нониусу, соответствующих данной точке свободной поверхности и положению иглы в центре сосуда (отсчет первой точки). Вычисляют отметку Z0теор. точки свободной поверхности относительно горизонтальной плоскости, проходящей через низшую точку свободной поверхности, при этом значение берется равным предыдущему, т.е. r = rтеор. 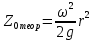 Отметку Z0опыт вычисленную на основании экспериментальных данных, сопоставляют с величиной Z0теор найденной расчетом. Расхождение в процентах подсчитывают по формуле: 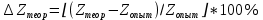 Занести полученные данные в таблицу 2. Провести построение теоретической и экспериментальной кривых свободной поверхности жидкости 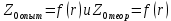 Вычисляем отметку Z0опыт для W1= 7,33 рад/с 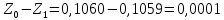 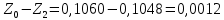 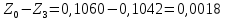 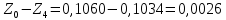 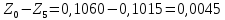 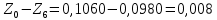 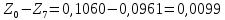 Вычисляем отметку Z0опыт для W2= 11,52 рад/с 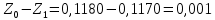 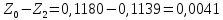 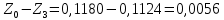 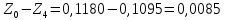 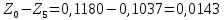 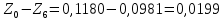 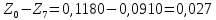 Вычисляем отметку Z0теор для W1= 7,33 рад/с 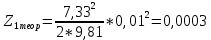 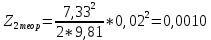 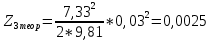 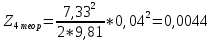 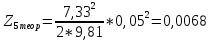 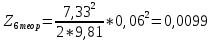 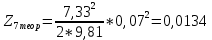 Вычисляем отметку Z0теор для W2= 11,52 рад/с 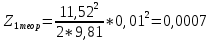 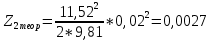 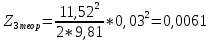 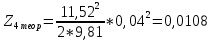 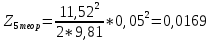 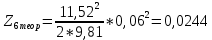 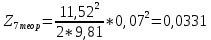 Расхождение в процентах для W1= 7,33 рад/с 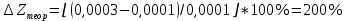 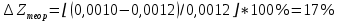 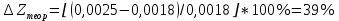 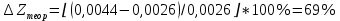 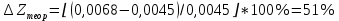 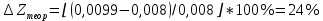 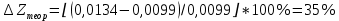 Расхождение в процентах для W2= 11,52 рад/с 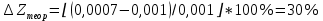 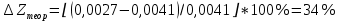 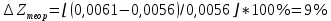 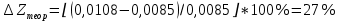 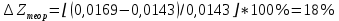 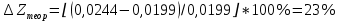 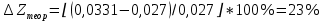 Графики  Для W1= 7,33 рад/с 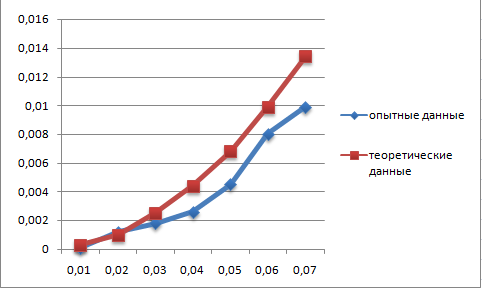 Для W2= 11,52 рад/с 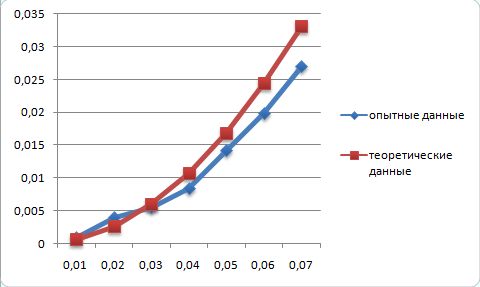 Таблица 2
Вывод: изучили относительный покой жидкости во вращающемся сосуде путем экспериментального нахождения координат точек кривой свободной поверхности жидкости. Было выявлено, что при частоте вращения W1=7,33 погрешность больше, чем при частоте вращения W2=11,52. Это связано с тем, что при большой частоте вращения жидкость поднимается по стенкам сосуда, все сильнее оголяя дно. Контрольные вопросы 1.Как получить уравнение свободной поверхности жидкости при вращении сосуда с жидкостью вокруг вертикальной оси (вывод). В случае равномерного вращения цилиндрического сосуда вокруг вертикальной оси с угловой скоростью ω уравнение любой изобарической поверхности (р = const) имеет вид: 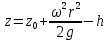 где z — координата точки пересечения свободной поверхности с осью вращения. 2. Какой вид имеет кривая свободной поверхности и сама поверхность? Параболоид вращения 3. Зависит ли форма кривой свободной поверхности от свойств жидкости? Форма кривых свободной поверхности жидкости зависит от соотношения глубин 4. Какие внешние силы действуют на жидкость? Силы тяжести, центробежная сила. 5.Почему жидкость вращается вместе с сосудом? Благодаря силам трения стенки вращающегося сосуда будут вначале увлекать за собой жидкость, а по истечении некоторого промежутка времени вся жидкость начнет вращаться вместе с сосудом с той же угловой скоростью, находясь по отношению к стенкам сосуда в покое. Какой объем жидкости выльется из сосуда при известных диаметре сосуда, его высоте, числе оборотов и начальном заполнении? Объем жидкости, находящейся в параболоиде вращения равен половине объема цилиндра, той же высоты, что и вращающийся цилиндр. 7. Какое избыточное давление будет действовать в различных точках дна сосуда? Избыточное давление на горизонтальное дно сосуда определяется высотой столба жидкости h и плотностью жидкости. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||