ПРОЕКТ КАШАЕВ АНТОН. Опытная проверка газовых законов
 Скачать 457.56 Kb. Скачать 457.56 Kb.
|
|
ВВЕДЕНИЕ ФИЗИКА - одна из основных областей естествознания - наука о свойствах и строении материи, о формах её движения и изменениях, об общих закономерностях явлений природы. Основой изучения физики являются законы, которые помимо своего теоретического описания требуют еще и практического (экспериментального) подтверждения. Нам известно на настоящий момент три основных способа такого практического подтверждения: натурное, математическое моделирование и компьютерный практикум. В древности физические законы подтверждались только экспериментальными исследованиями. Первоначально это были натурные исследования, а именно - практические подтверждения законов физики с помощью опытов. В дальнейшем, по мере развития математики, эти исследования дополнялись математическими подтверждениями законов физики, а именно - формулами и графиками. По мере дальнейшего развития человечества, когда на помощь людям смогли прийти такие передовые технологии, как компьютерные, изучение законов физики и их подтверждение еще более облегчилось для человека, так как ему на помощь пришла такая умная машина как компьютер. Нас окружает реальный газ – воздух, который при условиях, близких к нормальным (р ≈ 105 Па, t≈00С), является простейшей термодинамической системой. Состояние термодинамической системы можно охарактеризовать набором термодинамических параметров: температурой, давлением, объемом, массой или количеством вещества. Эти параметры называют макроскопическими, их можно измерить при помощи физических приборов: термометра, манометра и т.п. Макропараметры термодинамической системы, находящейся в состоянии термодинамического равновесия, не могут принимать произвольные значения - они связаны между собой определенными отношениями. Основная задача молекулярно-кинетической теории – нахождение уравнения состояния того или иного тела, находящегося в жидком или газообразном состоянии, является чрезвычайно сложной и до сих пор не решена. Точное ее решение получено лишь для единственной системы – идеального газа. Поэтому при объяснении свойств реального газа рассматривают его упрощенную модель – идеальный газ, молекулы которого не взаимодействуют на расстоянии, имеют малые размеры по сравнению со средним расстоянием между ними и соударяются как абсолютно упругие шарики. Процессы, в которых масса идеального газа и один из параметров - давление, объем или температура - остается постоянным, а изменяются только остальные два, называют изопроцессами. Если неизменным параметром является температура, то соответствующий изопроцесс называется изотермическим, если объем - изохорным, а если давление - изобарным. Экспериментально законы для этих условий изменения состояния газа были открыты учеными физиками в XVII – XIX веках. Выбор темы проекта определяется желанием и возможностью экспериментально с помощью лабораторного оборудования школьного кабинета физики воспроизвести эксперименты ученых и доказать справедливость газовых законов для реального газа – воздуха. Главной особенностью выбранной темы проекта является доступность оборудования и исследуемых материалов. Проблема проекта – экспериментальное исследование газовых законов различными способами, получение графических зависимостей: р(V) при изотермическом, р(Т) при изохорном, V(Т) при изобарных процессах на основании экспериментальных данных и доказательство справедливости газовых законов для реального газа – воздуха. Решив данную проблему, я получу конкретный образовательный результат: экспериментально исследую изотермический, изохорный и изобарный процессы различными способами и докажу справедливость газовых законов для реального газа - воздуха. Тема проекта актуальна, т.к. в разделе «Молекулярная физика и термодинамика» (10 класс) молекулярно – кинетической теории газа посвящена целая глава, а лабораторная работа предлагается только одна - по исследованию закона Бойля-Мариотта с помощью мензурки с водой, пробирки и измерительной ленты. При выполнении этой работы получается большая погрешность измерения не позволяющая доказать равенство р1V1=р2V2. Лабораторное оборудование школьного кабинета физики: набор для исследования изопроцессов в газах (автор изделия к.п.н. Степанов С.В., 2011 г.) и прибор для изучения газовых законов (ПГЗ-1, 1991 г.), напротив, позволяют с большой точностью провести проверку всех трех газовых законов. Цель проекта: решить проблему экспериментальной проверки разными способами справедливости газовых законов: Бойля-Мариотта, Шарля и Гей-Люссака. Достижение цели проекта позволит решить исходную проблему, т.к. полученные экспериментально данные при исследовании газовых законов различными способами позволят получить графические зависимости: р(V) при изотермическом, р(Т) при изохорном, V(Т) при изобарном процессах, согласующиеся с теоретическими данными параграфа учебника и доказать справедливость газовых законов для реального газа – воздуха. Проектные продукты - дидактический материал «Способы экспериментального исследования и проверки газовых законов» для школьного кабинета физики.Этот продукт поможет достичь цели проекта, т.к. будет содержать описание эксперимента по проверке справедливости каждого из законов: Бойля-Мариотта, Шарля и Гей-Люссака двумя способами, дающими одинаково верный результат. На достижение поставленной цели направлено решение следующих задач: 1. используя первоисточник – школьный учебник физики, сформировать представление о газовых законах; 2. выполнить эксперименты № 1-6 «Опытная проверка закона Бойля-Мариотта», «Опытная проверка закона Гей-Люссака», «Опытная проверка закона Шарля»; 3. сравнить полученные результаты, представить результаты измерений с помощью таблицы и графика; 4. сделать вывод о справедливости газовых законов для реального газа – воздуха; 5. познакомить одноклассников со способами исследования газовых законов, не описанных в учебнике, и результатами экспериментов. Методы работы над проектом: поисковый - выбор темы проекта, сбор и обработка информации, отбор необходимого лабораторного оборудования; конструкторский - поиск оптимального решения задач проекта, отбор материала для создания презентации; исследовательский – выполнение экспериментов; технологический - создание презентации; креативный – презентация реализации проекта (защита проекта); рефлексивный - анализ результатов, оценка качества работы автора проекта, возможная корректировка и применение данного материала в дальнейшей работе и учебе. Новизной работы является совершенствование исследовательских навыков при проведении экспериментов различными способами, позволяющих получить одинаковые результаты, доказывающие справедливость газовых законов для реального газа – воздуха. Объект исследования – газовые законы. База – кабинет физики МОУ «СОШ с.Студенки Белинского района Пензенской области им. А.И. Бородина» Ожидаемые результаты: 1) экспериментальное исследование изотермического, изохорного и изобарного процессов различными способами, 2) представление результатов измерений с помощью таблиц и графиков, 3) применение полученных в результате исследований результатов. Практическая значимость проекта: Пополнение дидактического материала кабинета физики разработкой «Способы экспериментального исследования и проверки газовых законов». Привлечение внимания учащихся к освоению действий, связанных с экспериментом. Развитие интереса к предмету физика. 2.ЛИТЕРАТУРНЫЙ ОБЗОР 2.1 ТЕОРИЯ ГАЗОВЫХ ЗАКОНОВ Идеальный газ – математическая модель газа, в которой в рамках молекулярно-кинетической теории предполагается, что: потенциальной энергией взаимодействия частиц, составляющих газ, можно пренебречь по сравнению с их кинетической энергией; суммарный объём частиц газа пренебрежимо мал; между частицами нет дальнодействующих сил притяжения или отталкивания, соударения частиц между собой и со стенками сосуда абсолютно упруги; время взаимодействия между частицами пренебрежимо мало по сравнению со средним временем между столкновениями.[4] В расширенной модели идеального газа, частицы, из которых он состоит, имеют форму упругих сфер или эллипсоидов, что позволяет учитывать энергию не только поступательного, но и вращательно-колебательного движения, а также не только центральные, но и нецентральные столкновения частиц. В рамках термодинамики идеальными называются гипотетические (реально не существующие) газы, подчиняющиеся термическому уравнению состояния Клапейрона-Менделеева. Модель широко применяется для решения задач термодинамики газов и задач аэрогазодинамики. Например, воздух при атмосферном давлении и комнатной температуре с большой точностью описывается данной моделью. В случае экстремальных температур или давлений требуется применение более точной модели, например модели газа Ван-дер-Ваальса, в котором учитывается притяжение между молекулами. Различают классический идеальный газ и квантовый идеальный газ. Классический идеальный газ. Свойства идеального газа на основе молекулярно-кинетических представлений определяются исходя из физической модели идеального газа, в которой приняты следующие допущения: объём частицы газа равен нулю (то есть диаметр молекулы d пренебрежимо мал по сравнению со средним расстоянием между ними, 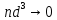 ; ;импульс передается только при соударениях (то есть силы притяжения между молекулами не учитываются, а силы отталкивания возникают только при соударениях); суммарная энергия частиц газа постоянна (то есть, нет передачи энергии за счет передачи тепла или излучением) В этом случае частицы газа движутся независимо друг от друга, давление газа на стенку равно сумме импульсов в единицу времени, переданной при столкновении частиц со стенкой, энергия – сумме энергий частиц газа. Свойства идеального газа описываются уравнением Менделеева-Клапейрона: 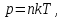 где p – давление, n – концентрация частиц, k – постоянная Больцмана, T – абсолютная температура. Равновесное распределение частиц классического идеального газа по состояниям описывается распределением Больцмана: 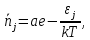 где 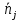 – среднее число частиц, находящихся в j-ом состоянии с энергией – среднее число частиц, находящихся в j-ом состоянии с энергией 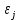 , а константа a определяется условием нормировки: , а константа a определяется условием нормировки: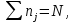 где N – полное число частиц. Распределение Больцмана является предельным случаем (квантовые эффекты пренебрежимо малы) распределений Ферми-Дирака и Бозе-Эйнштейна, и, соответственно, классический идеальный газ является предельным случаем Ферми-газа и Бозе-газа. Для любого идеального газа справедливо соотношение Майера: 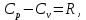 где R - универсальная газовая постоянная, 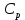 - молярная теплоемкость при постоянном давлении, - молярная теплоемкость при постоянном давлении, 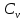 молярная теплоемкость при постоянном объёме. молярная теплоемкость при постоянном объёме.Квантовый идеальный газ. Понижение температуры и увеличение плотности газа может привести к ситуации, когда среднее расстояние между частицами становится соизмеримым с длинной волны де Бройля для этих частиц, что приводит к переходу от классического к квантовому идеальному газу. В таком случае поведение газа зависит от спина частиц: в случае полуцелого спина (фермионы) действует статистика Ферми-Дирака (Ферми-газ), в случае целого спина (бозоны) – статистика Бозе-Эйнштейна (Бозе-газ). Ферми-газ. Для фермионов действует принцип Паули, запрещающий двум тождественным фермионам находиться в одном квантовом состоянии. Вследствие этого при абсолютном нуле температуры импульсы частиц и, соответственно, давление и плотность энергии Ферми-газа отличны от нуля и пропорциональны числу частиц в единице объёма. Существует верхний предел энергии, который могут иметь частицы Ферми-газа при абсолютном нуле (Энергия Ферми 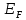 ). Если энергия теплового движения частиц Ферми-газа значительно меньше энергии Ферми, то это состояние называют вырожденным газом. ). Если энергия теплового движения частиц Ферми-газа значительно меньше энергии Ферми, то это состояние называют вырожденным газом.Особенностью Ферми-газов является крайне слабая зависимость давления от температуры: в нерелятивистском случае давление 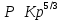 , в релятивистском – , в релятивистском – 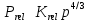 . .Примерами Ферми-газов являются электронный газ в металлах, сильнолегированных и вырожденных полупроводниках, вырожденный газ электронов в белых карликах и вырожденный газ нейтронов в нейтронных звёздах. Бозе-газ. Так как на бозоны принцип Паули не распространяется, то при снижении температуры Бозе-газа ниже некоторой температуры 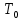 возможен переход бозонов на наинизший энергетический уровень с нулевым импульсом, то есть образование конденсата Бозе-Эйнштейна. Поскольку давление газа равно сумме импульсов частиц, переданной стенке в единицу времени, при возможен переход бозонов на наинизший энергетический уровень с нулевым импульсом, то есть образование конденсата Бозе-Эйнштейна. Поскольку давление газа равно сумме импульсов частиц, переданной стенке в единицу времени, при 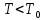 давление Бозе-газа зависит только от температуры. давление Бозе-газа зависит только от температуры.Примерами Бозе-газов являются различного рода газы квазичастиц (слабых возбуждений) в твёрдых телах и жидкостях, сверхтекучая компонента гелия II, конденсата Бозе-Эйнштейна куперовских электронных пар при сверхпроводимости. Примером ультрарелятивистского Бозе-газа является фотонный газ.[2] Реальный газ – это газ, свойства которого существенно зависят от взаимодействия молекул. В обычных условиях, когда средняя потенциальная энергия взаимодействия молекул много меньше их средней кинетической энергии, свойства реальных газов незначительно отличаются от свойств идеального газа и к реальным газам применимы законы, установленные для идеального газа. Отличие свойств реального газа от свойств идеального становится особенно значительным при высоких давлениях и низких температурах, когда начинают проявляться квантовые эффекты. В модели идеального газа не учитывается собственный объем молекул и силы межмолекулярного взаимодействия. Тщательная экспериментальная проверка газовых законов современными методами показала, что эти законы достаточно точно описывают поведение реальных газов при небольших давлениях и высоких температурах. При других условиях наблюдаются значительные отступления от этих законов. Причина заключается в том, что, во-первых, при очень сильном сжатии газов объем незанятого молекулами пространства становится сравним с объемом, занимаемым самими молекулами; а во-вторых, при низких температурах становится заметным взаимодействие между молекулами. Поэтому для описания поведения газа при достаточно больших плотностях уравнения состояния идеального газа не пригодны. Наличие сил межмолекулярного взаимодействия, а именно сил отталкивания, действующих на малых расстояниях порядка размеров молекул, и сил притяжения, приводит к сложной зависимости энергии потенциального взаимодействия молекул от расстояния. Для описания термодинамических свойств реальных газов используются различные уравнения состояния. При малых плотностях наличие межмолекулярного взаимодействия учитывается вириальным уравнением состояния реального газа: pV = RT[1 + B(T)/v + C(T)/v2 + ...], где p – давление, v – мольный объем, Т – абсолютная температура, R – газовая постоянная, В(Т), С(Т) и т. д. – вириальные коэффициенты, зависящие от температуры и характеризующие парные, тройные и т. д. взаимодействия частиц в газе. Качественно верно описывает основные отличия реального газа от идеального уравнение Ван-дер-Ваальса, учитывающее существование сил притяжения между молекулами, действие которых приводит к уменьшению давления газа, и сил отталкивания, препятствующих безграничному сжатию газа. Кроме уравнения Ван-дер-Ваальса было предложено много других эмпирических уравнений состояния реальных газов. Некоторые из них дают лучшее согласие с опытом за счет большого числа входящих в них феноменологических постоянных. Однако при качественном исследовании поведения реальных газов использование уравнения Ван-дер-Ваальса более удобно, благодаря его простоте и понятному физическому смыслу. Одной из основных характеристик реальных газов являются размеры молекул. В реальных газах их называют газокинетическими радиусами, и их размер связан с характерными расстояниями, на которых проявляются силы межатомных и межмолекулярных взаимодействий. В реальных газах возникают неоднородности полей давления и температуры, а также макроскопические потоки, которые приводят к переносу массы – диффузии. Для реальных газов характерна теплопроводность и вязкость. Главная особенность кинетических процессов переноса в реальных газах (в отличие от жидкостей и твердых тел) – наличие механизма столкновения молекул. Поэтому основной характеристикой этих процессов в газах является длина свободного пробега. Внутренняя энергия реального газа зависит от объема V, то есть от расстояния между молекулами, так как потенциальная энергия молекул определяется их взаимным расположением. Существование межмолекулярного взаимодействия в той или иной степени сказывается на всех свойствах реальных газов.[5] ОСНОВНОЕ УРАВНЕНИЕ МКТ Величина, измеряемая силой, действующей перпендикулярно на единицу площади поверхности тела, называется давлением. Согласно определению, давлении 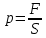 . Ниже приводятся единицы давления и соотношения между ними: . Ниже приводятся единицы давления и соотношения между ними:1 н/м2, 1 атм, 1 ат, 1 мм рт. ст. 1 атм = 760 мм рт. ст. = 1,01*105 н/м2. 1 ат = 9,81*104 н/м2. 1 мм рт. ст. = 133 н/м2. Давление газа на стенки сосуда – это сила, действующая перпендикулярно на единицу площади последнего. Причиной давления являются удары молекул о стенки сосуда. Сила удара одной молекулы пренебрежительно мала, но большое число ударов огромного количества молекул создает заметное давление газа на стенки сосуда. Выведем упрощенно формулу, по которой вычисляется давление идеального газа на стенки сосуда. Допустим, что имеется прямоугольный цилиндр с поршнем, который может двигаться без трения (рис. 1). 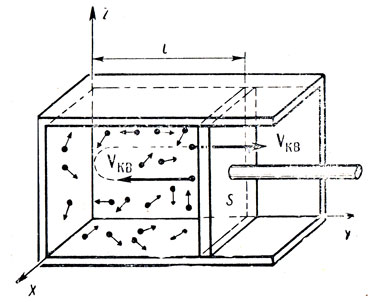 Рис. 1. К выводу основного уравнения кинетической теории газов. Давление газа на поршень 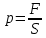 . Найдем общую силу удара F молекул о поршень. Для этого первоначально по второму закону Ньютона найдем силу одного удара одной молекулы о поршень: F1 = Ma, где М – масса поршня, а – ускорение, с которым будет двигаться поршень. Умножив силу F1 на число молекул, движущихся вдоль оси Y, найдем общую силу удара молекул о поршень. . Найдем общую силу удара F молекул о поршень. Для этого первоначально по второму закону Ньютона найдем силу одного удара одной молекулы о поршень: F1 = Ma, где М – масса поршня, а – ускорение, с которым будет двигаться поршень. Умножив силу F1 на число молекул, движущихся вдоль оси Y, найдем общую силу удара молекул о поршень.Пусть на покоящийся поршень летит перпендикулярно к нему молекула с массой m и скоростью v. За время продолжительности удара t скорость поршня изменится от v0 = 0 до v1, и он получает ускорение 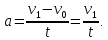 Так как поршень движется очень медленно, а молекула очень быстро, то можно некоторое время пренебрегать увеличением расстояния t и считать что удары молекулы о поршень следуют друг за другом через равные промежутки времени 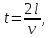 в течение которого происходит изменение скорости v1. в течение которого происходит изменение скорости v1.До удара молекулы сумма импульсов ее и поршня равна mv. Удар молекулы о поршень вполне упругий, поэтому после удара она будет иметь импульс –mv, а поршень Mv1. Сумма их импульсов: -mv + Mv1. По закону сохранения импульса mv = -mv + Mv1 или 2mv = Mv1. Отсюда скорость, которую получил поршень, 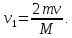 C каждым новым ударом молекулы поршень через равные промежутки времени t будет увеличивать свою скорость на величину 2mv/M. Тогда ускорение поршня: C каждым новым ударом молекулы поршень через равные промежутки времени t будет увеличивать свою скорость на величину 2mv/M. Тогда ускорение поршня: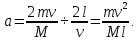 Сила одного удара молекулы о поршень: 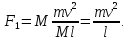 Ввиду хаотичности движения молекул по всем трем направлениям осей координат движется одинаковое количество молекул. Из общего числа n всех молекул 1/3 двигалась прямолинейно между поршнем и противоположной ему стенкой, 1/3 молекул – между верхней и нижней стенками и 1/3 – между дальней и ближней стенками. Все три направления одинаково вероятны. Тогда сила давления молекул на поршень: 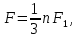 или 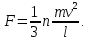 Давление газа на поршень: 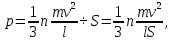 где lS = V – объем газа. Тогда 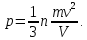 Здесь 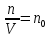 – число молекул в единице объема газа. Следовательно,: – число молекул в единице объема газа. Следовательно,: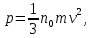 где v - средняя квадратичная скорость. Эта формула называется основным уравнением кинетической теории идеального газа для давления. Давление газа равно 1/3 произведения массы молекулы, числа молекул в единице объема и квадрату средней квадратичной скорости молекулы газа. [1] 2.3 ЗАКОНЫ ИДЕАЛЬНЫХ ГАЗОВ Газы, подчиняющиеся законам Бойля-Мариотта, Гей-Люссака, Авогадро и Дальтона, называются идеальными. Эти законы и соотношения, построенные на их основе, можно применять также к реальным газам при сравнительно невысоких давлениях и сравнительно высоких температурах. С молекулярно-кинетической точки зрения идеальный газ – это газ, в котором отсутствуют силы взаимодействия между молекулами и пренебрегают объемом самих молекул. Закон Бойля-Мариотта. При постоянной массе и одной и той же температуре плотность идеального газа изменяется прямо пропорционально, а удельный объем – обратно пропорционально давлению газа: 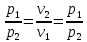 или 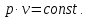 Закон Гей-Люссака. При постоянных давлении и массе удельный объем идеального газа изменяется прямо пропорционально, а его плотность - обратно пропорционально абсолютной температуре газа: 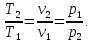 При объединении законов Бойля-Мариотта и Гей-Люссака получают уравнение Клапейрона для 1 кг газа: 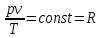 или 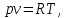 где R – газовая постоянная. Размерность R , в соответствии с последним уравнением, 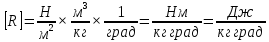 показывает, что эта величина является работой 1кг газа при постоянном давлении и изменении его температуры на 1К. Для идеального газа величина R зависит только от природы рабочего вещества. Таким образом, уравнение Клапейрона связывает три основных термодинамических параметра: p, v, T и обычно используется для определения неизвестного параметра по двум заданным. Поэтому оно называется уравнением состояния идеального газа или его характеристическим уравнением. Для G кг газа уравнение состояния: 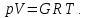 Закон Авогадро. При одинаковых температурах и давлениях в равных объёмах различных идеальных газов содержится одинаковое количество молекул. Масса газа в килограммах, численно равная молекулярной массе, называется: килограмм-молекула или киломоль (кмоль). Из закона Авогадро следует, что произведение 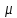 v (т.е. объём одного киломоля, где v (т.е. объём одного киломоля, где 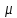 кг/кмоль – молекулярная масса однородного газа, а для смеси кажущаяся молекулярная или средняя молекулярная масса) есть величина одинаковая для всех газов и газовых смесей при одинаковых p и T. При нормальных физических условиях кг/кмоль – молекулярная масса однородного газа, а для смеси кажущаяся молекулярная или средняя молекулярная масса) есть величина одинаковая для всех газов и газовых смесей при одинаковых p и T. При нормальных физических условиях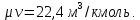 Уравнение состояния для 1 кмоль газа называется уравнением Клапейрона-Менделеева и имеет вид 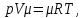 где V = V, при этом 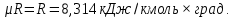 Величина R 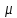 является универсальной газовой постоянной, одинаковой для киломоля любого однородного газа или газовой смеси. Универсальная газовая постоянная для 1кг газа (R) определяется из соотношения [3] является универсальной газовой постоянной, одинаковой для киломоля любого однородного газа или газовой смеси. Универсальная газовая постоянная для 1кг газа (R) определяется из соотношения [3]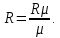 3. ПРАКТИЧЕСКАЯ ЧАСТЬ 3.1 ЛАБОРАТОРНОЕ ОБОРУДОВАНИЕ В настоящее время эксперименты, позволяющие определить, как связаны между собой макропараметры (давление, объем и температура) простейшей термодинамической системы – идеального газа можно провести в школьной лаборатории на установке (рис. 1), состоящей наполненного газом (воздухом) гофрированного сосуда (1), соединенного с манометром (2), которым измеряют давление газа внутри сосуда. Объем газа изменяется при помощи винта (3). Сосуд с газом помещен в ванну с водой (4), температуру которой контролируют термометром. А можно с помощью более современного оборудования – набора для исследования изопроцесов в газах, производственно-методического центра «Дидакт» (рис.2). Основу набора составляет пластиковая эластичная длинная трубка-резервуар с воздушными кранами на концах (1), внутри которой воздух – исследуемый газ, и
|


