лабораторная работа 10ОПРЕДЕЛЕНИЕ ГОРИЗОНТАЛЬНОЙ СОСТАВЛЯЮЩЕЙ ВЕКТОРА ИНДУКЦИИ МАГНИТНОГО ПОЛЯ ЗЕМЛИ И ПЕРЕВОДНОГО МНОЖИТЕЛЯ Т. лаб10. Определение горизонтальной составляющей вектора индукции магнитного поля земли и переводного множителя тангенсгальванометра
 Скачать 1.09 Mb. Скачать 1.09 Mb.
|
|
Чувашский государственный университет имени И.Н.Ульянова Факультет радиоэлектроники и автоматики ОПРЕДЕЛЕНИЕ ГОРИЗОНТАЛЬНОЙ СОСТАВЛЯЮЩЕЙ ВЕКТОРА ИНДУКЦИИ МАГНИТНОГО ПОЛЯ ЗЕМЛИ И ПЕРЕВОДНОГО МНОЖИТЕЛЯ ТАНГЕНС-ГАЛЬВАНОМЕТРА ЛАБОРАТОРНАЯ РАБОТА 10 Выполнил: Студент гр. РЭА-41-21 Серейкин С. Ю. Проверил: Сорокин Г. М Чебоксары 2022г. Приборы и принадлежности: тангенс-гальванометр, амперметр, реостат, источник постоянного тока. Цель работы: ознакомление с основными количественными характеристиками магнитного поля Земли, определение горизонтальной составляющей индукции магнитного поля Земли (В0)по углу отклонения магнитной стрелки в результирующем магнитном поле Земли и тангенс-гальванометра. Теоретическое введение Земля представляет собой естественный магнит, полюса которого располагаются недалеко ( 300 км) от географических полюсов. Магнитный полюс Земли, который расположен на севере, называется Южным магнитным полюсом, другой, соответственно на юге, – Северным магнитным полюсом. Через магнитные полюса Земли можно провести линии больших кругов – магнитные меридианы, перпендикулярно к ним – линию большого круга – магнитный экватор – и параллельно последнему линии малых кругов – магнитные параллели. Таким образом, каждой точке на Земле будут соответствовать не только географические, но и магнитные координаты. Если в данной точке Земли свободно подвесить магнитную стрелку (т.е. подвесить за центр масс так, чтобы она могла поворачиваться и в горизонтальной и в вертикальной плоскостях), то она установится по направлению напряженности магнитного поля Земли в данной точке. Но так как магнитное поле Земли – это поле прямого магнита, я 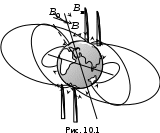 сно, что силовые линии этого поля лишь на магнитных полюсах вертикальны, а на магнитном экваторе горизонтальны. В любой другой точке земной поверхности силовая линия, касательная к ней индукция магнитного поля и, следовательно, свободно подвешенная стрелка располагаются под каким-то углом к вертикали в этой точке Земли и, значит, под каким-то углом к горизонтальной плоскости в данной точке (рис. 10.1). Из-за несовпадения магнитных и географических полюсов Земли не совпадают и плоскости магнитного и географического меридианов, проходящих через данную точку земной поверхности. Таким образом, положение свободно расположенной магнитной стрелки характеризуется двумя углами и , определенными для данной точки Земли. сно, что силовые линии этого поля лишь на магнитных полюсах вертикальны, а на магнитном экваторе горизонтальны. В любой другой точке земной поверхности силовая линия, касательная к ней индукция магнитного поля и, следовательно, свободно подвешенная стрелка располагаются под каким-то углом к вертикали в этой точке Земли и, значит, под каким-то углом к горизонтальной плоскости в данной точке (рис. 10.1). Из-за несовпадения магнитных и географических полюсов Земли не совпадают и плоскости магнитного и географического меридианов, проходящих через данную точку земной поверхности. Таким образом, положение свободно расположенной магнитной стрелки характеризуется двумя углами и , определенными для данной точки Земли.Магнитное склонение – угол между направлениями географического и магнитного меридианов (рис. 10.2). Различают восточное и западное склонение (северный полюс стрелки отклоняется соответственно вправо или влево от географического меридиана). Магнитное наклонение – угол между направлением напряженности магнитного поля в данной точке и горизонтальной плоскостью (рис. 10.3). Наклонение может быть северное или южное (северный или южный конец стрелки ниже горизонтальной плоскости). Эти два угла – склонение и наклонение – называют элементами земного магнетизма.  Магнитное поле Земли подвержено суточным, годовым, вековым и т.п. колебаниям. Соответственно меняются и элементы земного магнетизма. Магнитное поле Земли подвержено суточным, годовым, вековым и т.п. колебаниям. Соответственно меняются и элементы земного магнетизма. Описание экспериментальной установки                            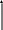          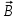 Источник постоянного тока s n 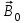 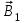 + 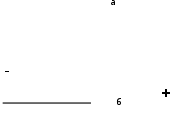 Рис. 10.4    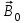 и поле и поле 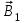 , созданное током. Под действием этих полей магнитная стрелка займет такое положение равновесия, при котором равнодействующая , созданное током. Под действием этих полей магнитная стрелка займет такое положение равновесия, при котором равнодействующая 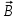 двух полей будет совпадать с линией, соединяющей полюса магнитной стрелки ns. двух полей будет совпадать с линией, соединяющей полюса магнитной стрелки ns. На рис. 10.4 – NS – направление магнитного меридиана Земли; а и б – сечения витка катушки горизонтальной плоскостью; ns – магнитная стрелка, помещенная в центре катушки; 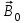 – вектор горизонтальной составляющей индукции поля Земли; – вектор горизонтальной составляющей индукции поля Земли; 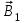 – вектор индукции магнитного поля, созданного током. Из рис. 10.4 видно, что – вектор индукции магнитного поля, созданного током. Из рис. 10.4 видно, что 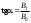 , а следовательно , а следовательно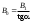 . (1) . (1)Величина индукции В1 поля, созданного током в центре катушки, рассчитывается по закону Био–Савара–Лапласа 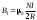 , ,где I - сила тока, текущего в витке; R - радиус витка; N - число витков; 0 - магнитная постоянная, равная 4*10-7 Гн/м. Подставляя В1 в формулу (1) получим 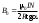 . (2) . (2)Этой формулой пользуются для опытного определения В0. Кроме того, из выражения (2) можно получить 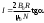 . (3) . (3)Анализ формулы (3) показывает, что сила тока в катушке пропорциональна тангенсу угла отклонения магнитной стрелки от горизонтальной составляющей вектора индукции магнитного поля Земли. Таким образом, этот прибор может служить также для измерения силы тока. В формуле (3) множитель 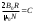 (4) (4)является постоянным для данного прибора, его называют переводным множителем тангенс-гальванометра. Таким образом, формулу (3) можно переписать так 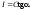 . (5) . (5)О 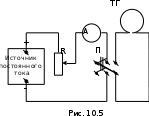 тсюда следует, что постоянная С численно равна тому току, который протекает по виткам, когда угол отклонения стрелки равен 45о. Для производства измерений пользуются схемой, представленной на рис. 10.5, где введены следующие обозначения: ТГ – тангенс-гальванометр, R – реостат, А – амперметр, П – переключатель. тсюда следует, что постоянная С численно равна тому току, который протекает по виткам, когда угол отклонения стрелки равен 45о. Для производства измерений пользуются схемой, представленной на рис. 10.5, где введены следующие обозначения: ТГ – тангенс-гальванометр, R – реостат, А – амперметр, П – переключатель.Из выражений (3) и (5) получаем 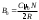 . (6) . (6)Порядок выполнения работы Собрать цепь по схеме рис. 10.5 и установить плоскость катушки в плоскости магнитного меридиана Земли (см. выше). Включив полностью реостат R, присоединить собранную цепь к зажимам источника постоянного напряжения. Задать необходимую силу тока в катушке реостатом. Дождаться, когда магнитная стрелка придет в равновесие. Отсчитать углы '1 и '2 по обоим концам стрелки для уничтожения эксцентриситета стрелки (несовпадение оси стрелки с центром шкалы) и записать в таблицу наблюдения уже средние из этих значений 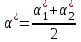 . Измерить силу тока по амперметру А. . Измерить силу тока по амперметру А.Не меняя силы тока, изменить его направление переключателем П и измерить величину " опять по обоим концам стрелки. Переключение направления тока необходимо производить для уничтожения возможной ошибки из-за неточной установки плоскости катушки в плоскости магнитного меридиана. Повторить опыт не менее 10 раз при различных силах тока. Сила тока может регулироваться изменением сопротивления реостата R. Результаты измерений и постоянные величины занести в таблицу 10.1. Таблица 10.1
Выписать ошибки прямых измерений и физических констант. Построить график I=f(tg). По графику найти значение С и по формуле (6) вычислить В0. Значение берется равным среднему арифметическому '1 и '2: 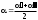 . .Расчет ошибок. За абсолютные погрешности прямых измерений взять приборные ошибки, т.е. 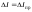 ; ;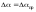 . .Относительные погрешности результатов косвенных измерений В0 и С найти по формулам 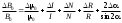 ; ;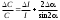 . .Записать результаты опытов в виде: 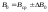 , ,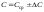 и сделать заключение по работе. 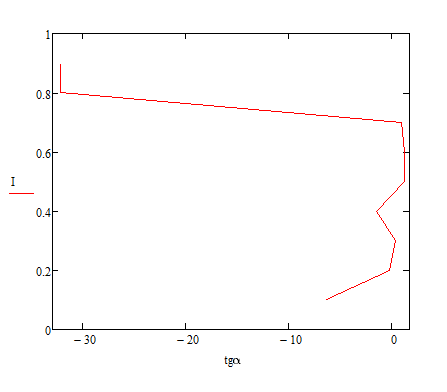 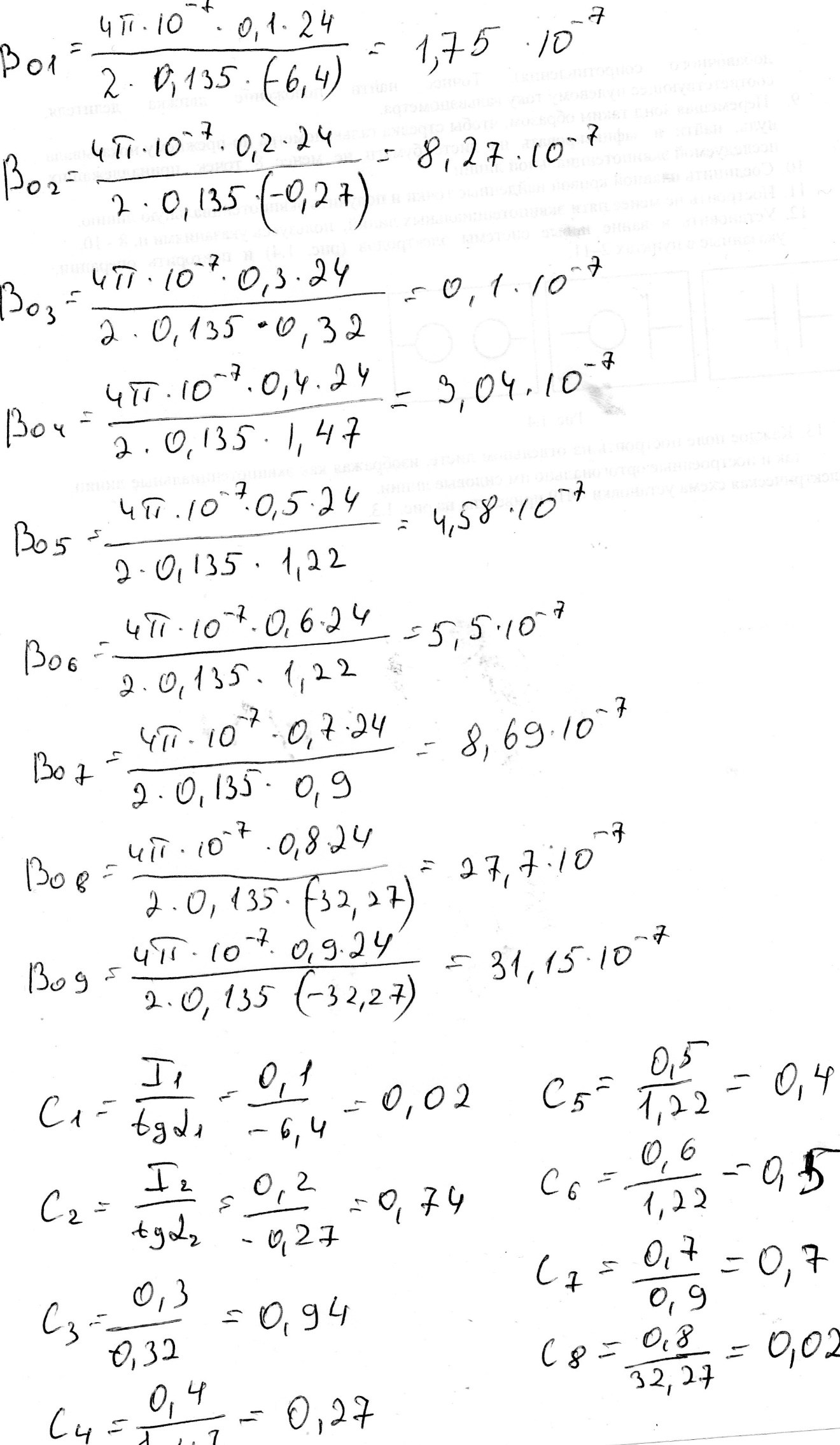 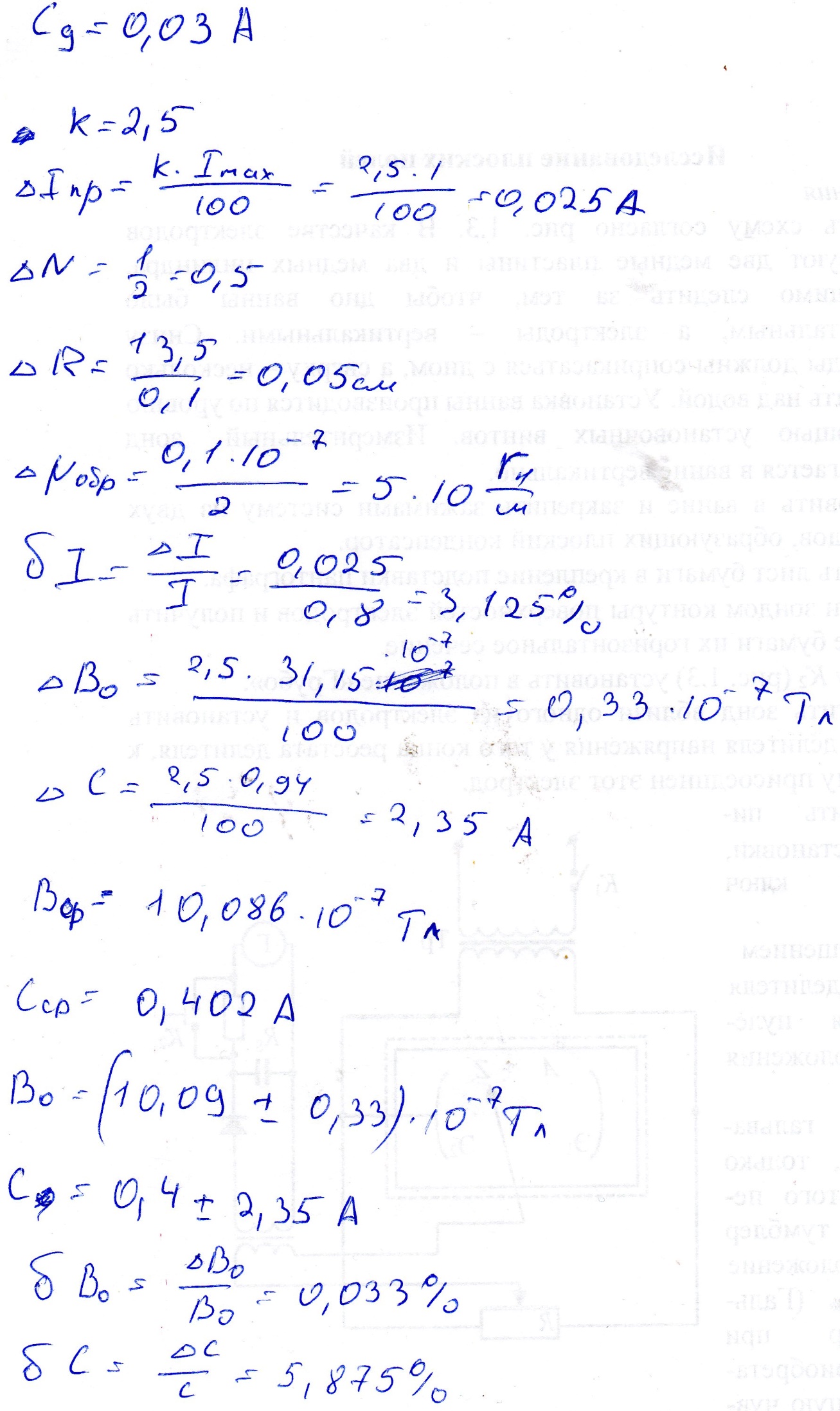 Вывод: ознакомился с основными количественными характеристиками магнитного поля Земли, определил горизонтальной составляющей индукции магнитного поля Земли (В0)по углу отклонения магнитной стрелки в результирующем магнитном поле Земли и тангенс-гальванометра. |
