1. Определение расстоянии и размеров тел в Солнечной системе. Определение расстоянии и размеров тел в Солнечной системе. Цель
 Скачать 4.14 Mb. Скачать 4.14 Mb.
|
|
Определение расстоянии и размеров тел в Солнечной системе. Цель: рассмотреть основные способы определения расстояний и размеров тел в Солнечной системе. 1. Форма и размеры Земли. Представление о Земле как о шаре, который свободно, без всякой опоры находится в космическом пространстве, является одним из величайших достижений науки древнего мира. Считается, что первое достаточно точное определение размеров Земли провёл греческий учёный Эратосфен (276–194 до н. э.), живший в Египте. Идея, положенная в основу измерений Эратосфена, весьма проста: измерить длину дуги земного меридиана в линейных единицах и определить, какую часть полной окружности эта дуга составляет. Получив эти данные, можно вычислить длину дуги в 1°, а затем длину окружности и величину её радиуса, т. е. радиуса земного шара. Очевидно, что длина дуги меридиана в градусной мере равна разности географических широт двух пунктов: ϕB-ϕA. 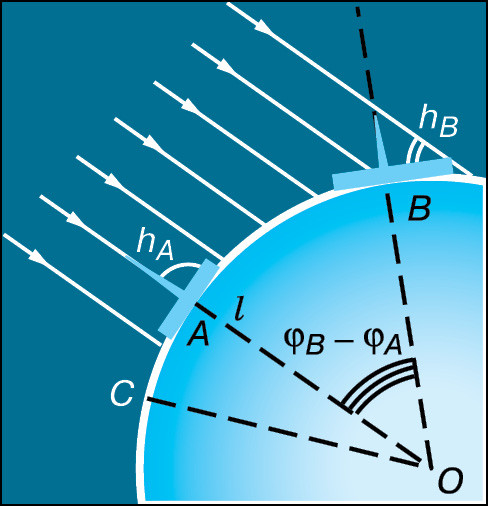 Рис. 1. Способ Эратосфена Для того чтобы определить эту разность, Эратосфен сравнил полуденную высоту Солнца в один и тот же день в двух городах, находящихся на одном меридиане. Измерив высоту Солнца hB (рис. 1) в полдень 22 июня в Александрии, где он жил, Эратосфен установил, что Солнце отстоит от зенита на 7,2°. В этот день в полдень в городе Сиена (ныне Асуан) Солнце освещает дно самых глубоких колодцев, т. е. находится в зените (hA = 90°). Следовательно, длина дуги составляет 7,2°. Расстояние между Сиеной (A) и Александрией (B) около 5000 греческих стадий – l. Стадией в Древней Греции считалось расстояние, которое проходит легко вооружённый греческий воин за тот промежуток времени, в течение которого Солнце, коснувшееся горизонта своим нижним краем, целиком скроется за горизонт. Несмотря на кажущееся неудобство такой единицы и достаточную громоздкость словесного определения, её введение выглядело вполне оправданным, учитывая, что строгая периодичность небесных явлений позволяла использовать их движение для счёта времени. Обозначив длину окружности земного шара через L, получим такое выражение: 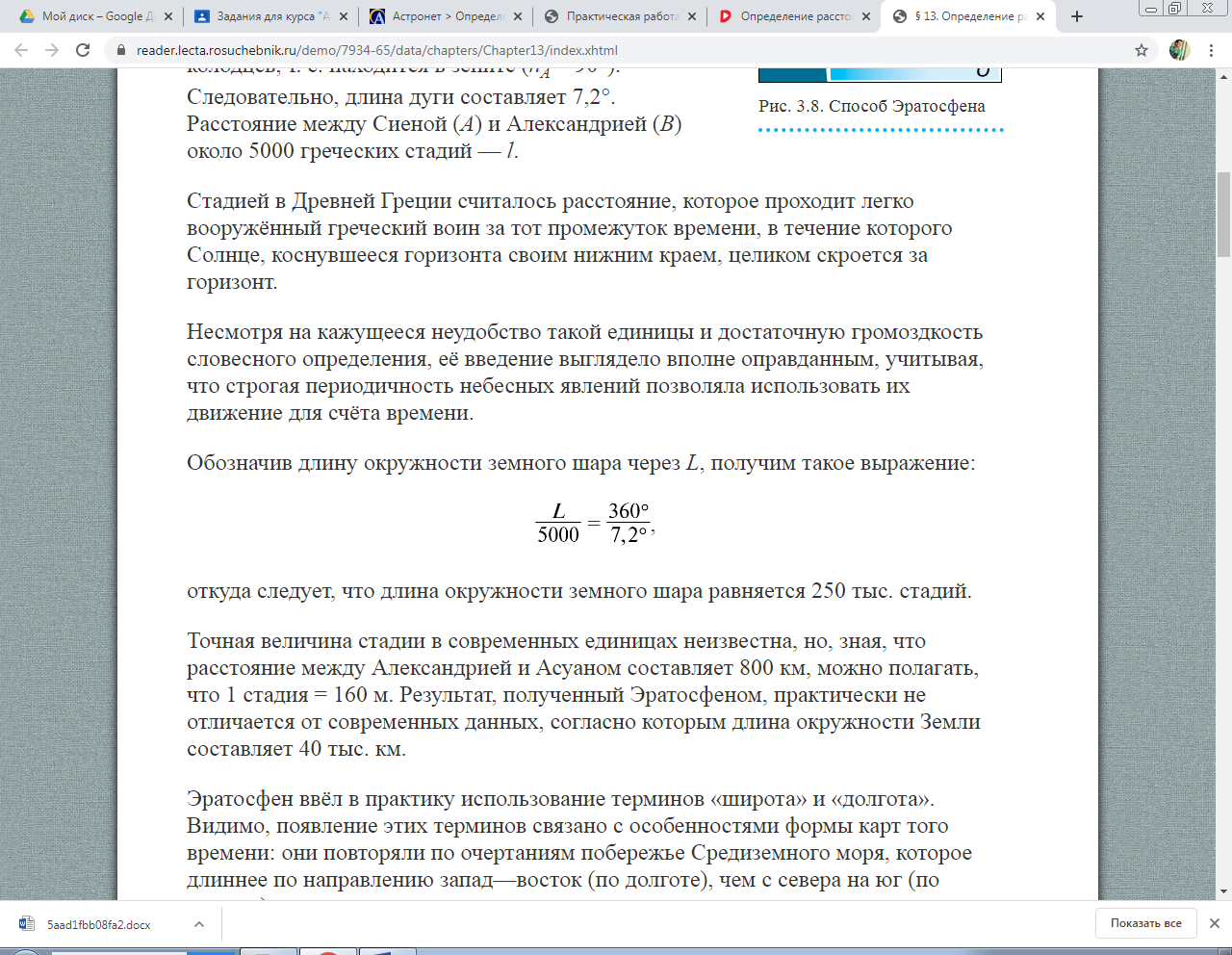 откуда следует, что длина окружности земного шара равняется 250 тыс. стадий. Точная величина стадии в современных единицах неизвестна, но, зная, что расстояние между Александрией и Асуаном составляет 800 км, можно полагать, что 1 стадия = 160 м. Результат, полученный Эратосфеном, практически не отличается от современных данных, согласно которым длина окружности Земли составляет 40 тыс. км. Эратосфен ввёл в практику использование терминов «широта» и «долгота». Видимо, появление этих терминов связано с особенностями формы карт того времени: они повторяли по очертаниям побережье Средиземного моря, которое длиннее по направлению запад–восток (по долготе), чем с севера на юг (по широте). 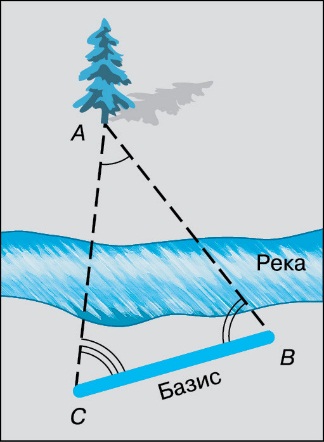 Рис. 2. Параллактическое смещение Определить географическую широту двух пунктов оказывается гораздо проще, чем измерить расстояние между ними. Зачастую непосредственное измерение кратчайшего расстояния между этими пунктами оказывается невозможным из-за различных естественных препятствий (гор, рек и т. п.). Поэтому применяется способ, основанный на явлении параллактического смещения и предусматривающий вычисление расстояния на основе измерений длины одной из сторон (базиса – BC) и двух углов B и C в треугольнике ABC (рис. 2). Параллактическим смещением называется изменение направления на предмет при перемещении наблюдателя. Чем дальше расположен предмет, тем меньше его параллактическое смещение, и чем больше перемещение наблюдателя (базис измерения), тем больше параллактическое смещение. 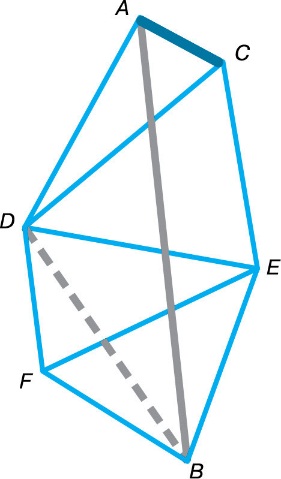 Рис. 3. Схема триангуляции Для определения длины дуги используется система треугольников – способ триангуляции, который впервые был применён ещё в 1615 г. Пункты в вершинах этих треугольников выбираются по обе стороны дуги на расстоянии 30–40 км друг от друга так, чтобы из каждого пункта были видны по крайней мере два других. Основой для вычисления длин сторон во всех этих треугольниках является размер базиса AC (рис. 3.10). Точность измерения базиса длиной в 10 км составляет около 1 мм. Во всех пунктах устанавливают геодезические сигналы – вышки высотой в несколько десятков метров. С вершины сигнала с помощью угломерного инструмента (теодолита) измеряют углы между направлениями на два-три соседних пункта. Измерив углы в треугольнике, одной из сторон которого является базис, геодезисты получают возможность вычислить длину двух других его сторон. Проводя затем измерение углов из пунктов, расстояние между которыми вычислено, можно узнать длину двух очередных сторон в треугольнике. Зная длину сторон этих треугольников, можно определить длину дуги AB. В какой степени форма Земли отличается от шара, выяснилось в конце XVIII в. Для уточнения формы Земли Французская академия наук снарядила сразу две экспедиции. Одна из них работала в экваториальных широтах Южной Америки в Перу, другая – вблизи Северного полярного круга на территории Финляндии и Швеции. Измерения показали, что длина одного градуса дуги меридиана на севере больше, чем вблизи экватора. Последующие исследования подтвердили, что длина дуги одного градуса меридиана увеличивается с возрастанием географической широты. Это означало, что форма Земли – не идеальный шар: она сплюснута у полюсов. Её полярный радиус на 21 км короче экваториального. Для школьного глобуса масштаба 1 : 50 000 000 отличие этих радиусов будет всего 0,4 мм, т. е. совершенно незаметно. Отношение разности величин экваториального и полярного радиусов Земли к величине экваториального называется сжатием. По современным данным, оно составляет 1/298 , или 0,0034. Это означает, что сечение Земли по меридиану будет не окружностью, а эллипсом, у которого большая ось проходит в плоскости экватора, а малая совпадает с осью вращения. В XX в. благодаря измерениям, точность которых составила 15 м, выяснилось, что земной экватор также нельзя считать окружностью. Сплюснутость экватора составляет всего 1/30000 (в 100 раз меньше сплюснутости меридиана). Более точно форму нашей планеты передаёт фигура, называемая эллипсоидом, у которого любое сечение плоскостью, проходящей через центр Земли, не является окружностью. В настоящее время форму Земли принято характеризовать следующими величинами:
2. Определение расстояний в Солнечной системе. Горизонтальный параллакс. Измерить расстояние от Земли до Солнца удалось лишь во второй половине XVIII в., когда был впервые определён горизонтальный параллакс Солнца. По сути дела, при этом измеряется параллактическое смещение объекта, находящегося за пределами Земли, а базисом является её радиус. Горизонтальным параллаксом ( p) называется угол, под которым со светила виден радиус Земли, перпендикулярный лучу зрения (рис. 4). 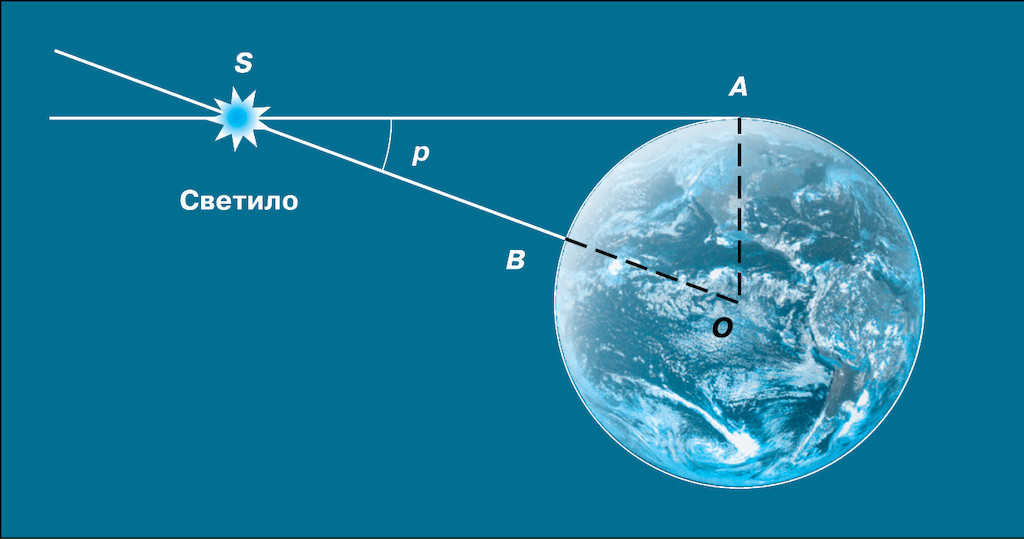 Рис. 4. Горизонтальный параллакс светила Из треугольника OAS можно выразить величину – расстояние OS = D:  , ,где R – радиус Земли. По этой формуле можно вычислить расстояние в радиусах Земли, а зная его величину, – выразить расстояние в километрах. Очевидно, что чем дальше расположен объект, тем меньше его параллакс. Наибольшее значение имеет параллакс Луны, который меняется в связи с тем, что Луна обращается по эллиптической орбите, и в среднем составляет 57ʹ. Параллаксы планет и Солнца значительно меньше. Так, параллакс Солнца равен 8,8ʺ. Такому значению параллакса соответствует расстояние до Солнца, примерно равное 150 млн км. Это расстояние принимается за одну астрономическую единицу (1 а. е.) и используется при измерении расстояний между телами Солнечной системы. Известно, что для малых углов sin p ≈ p, если угол p выражен в радианах. В одном радиане содержится 206 265ʺ. Тогда, заменяя sin p на p и выражая этот угол в радианной мере, получаем формулу в виде, удобном для вычислений: 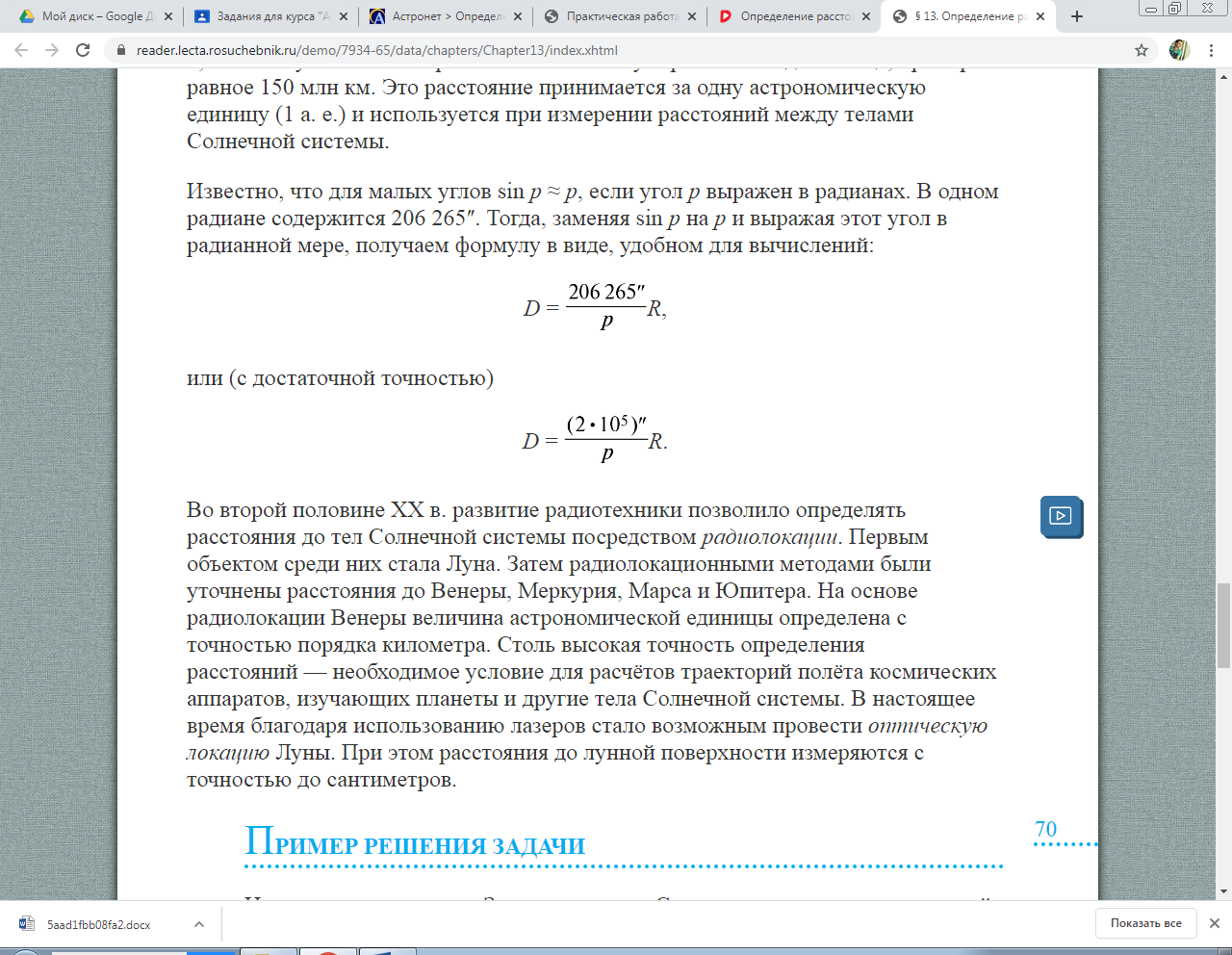 или (с достаточной точностью)  Во второй половине XX в. развитие радиотехники позволило определять расстояния до тел Солнечной системы посредством радиолокации. Первым объектом среди них стала Луна. Затем радиолокационными методами были уточнены расстояния до Венеры, Меркурия, Марса и Юпитера. На основе радиолокации Венеры величина астрономической единицы определена с точностью порядка километра. Столь высокая точность определения расстояний – необходимое условие для расчётов траекторий полёта космических аппаратов, изучающих планеты и другие тела Солнечной системы. В настоящее время благодаря использованию лазеров стало возможным провести оптическую локацию Луны. При этом расстояния до лунной поверхности измеряются с точностью до сантиметров. Пример решения задачи На каком расстоянии от Земли находится Сатурн, когда его горизонтальный параллакс равен 0,9ʺ?
Откуда 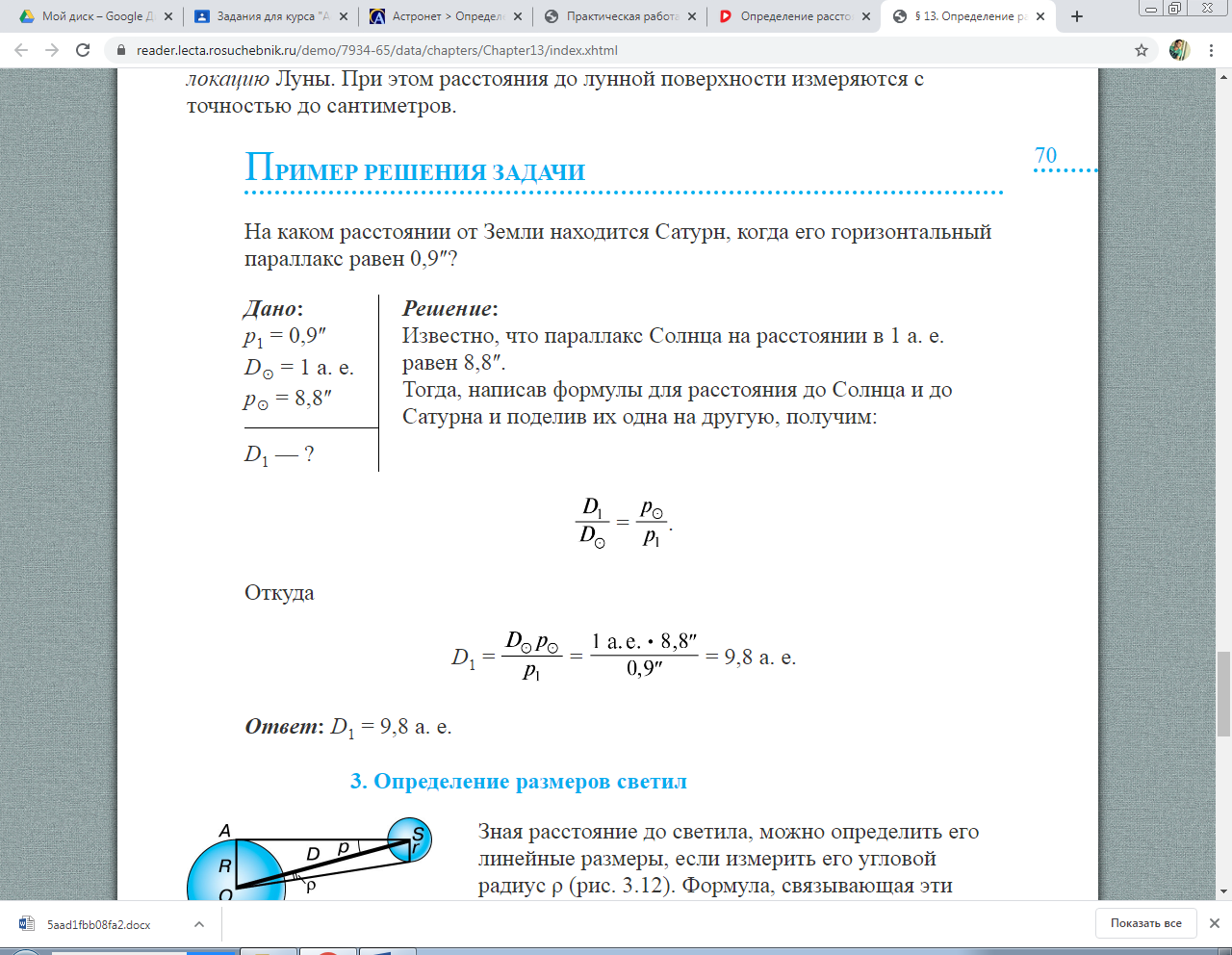 Ответ: D1 = 9,8 а. е. 3. Определение размеров светил  Рис. 5. Угловые размеры светила Зная расстояние до светила, можно определить его линейные размеры, если измерить его угловой радиус ρ (рис. 5). Формула, связывающая эти величины, аналогична формуле для определения параллакса: 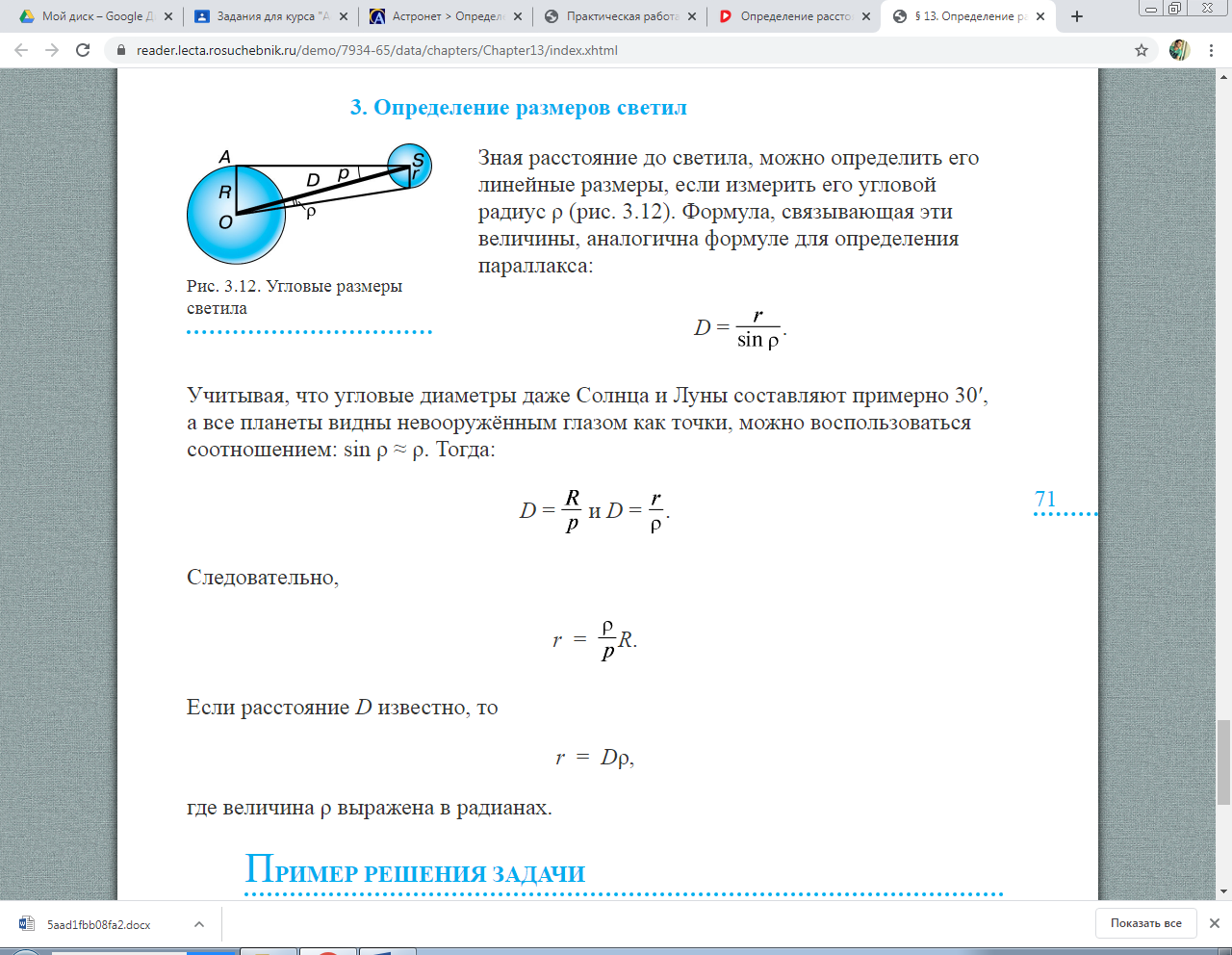 Учитывая, что угловые диаметры даже Солнца и Луны составляют примерно 30ʹ, а все планеты видны невооружённым глазом как точки, можно воспользоваться соотношением: sin ρ ≈ ρ. Тогда:  Следовательно,  Если расстояние D известно, то r=Dρ, где величина ρ выражена в радианах. Пример решения задачи Чему равен линейный диаметр Луны, если она видна с расстояния 400 000 км под углом примерно 30ʹ?
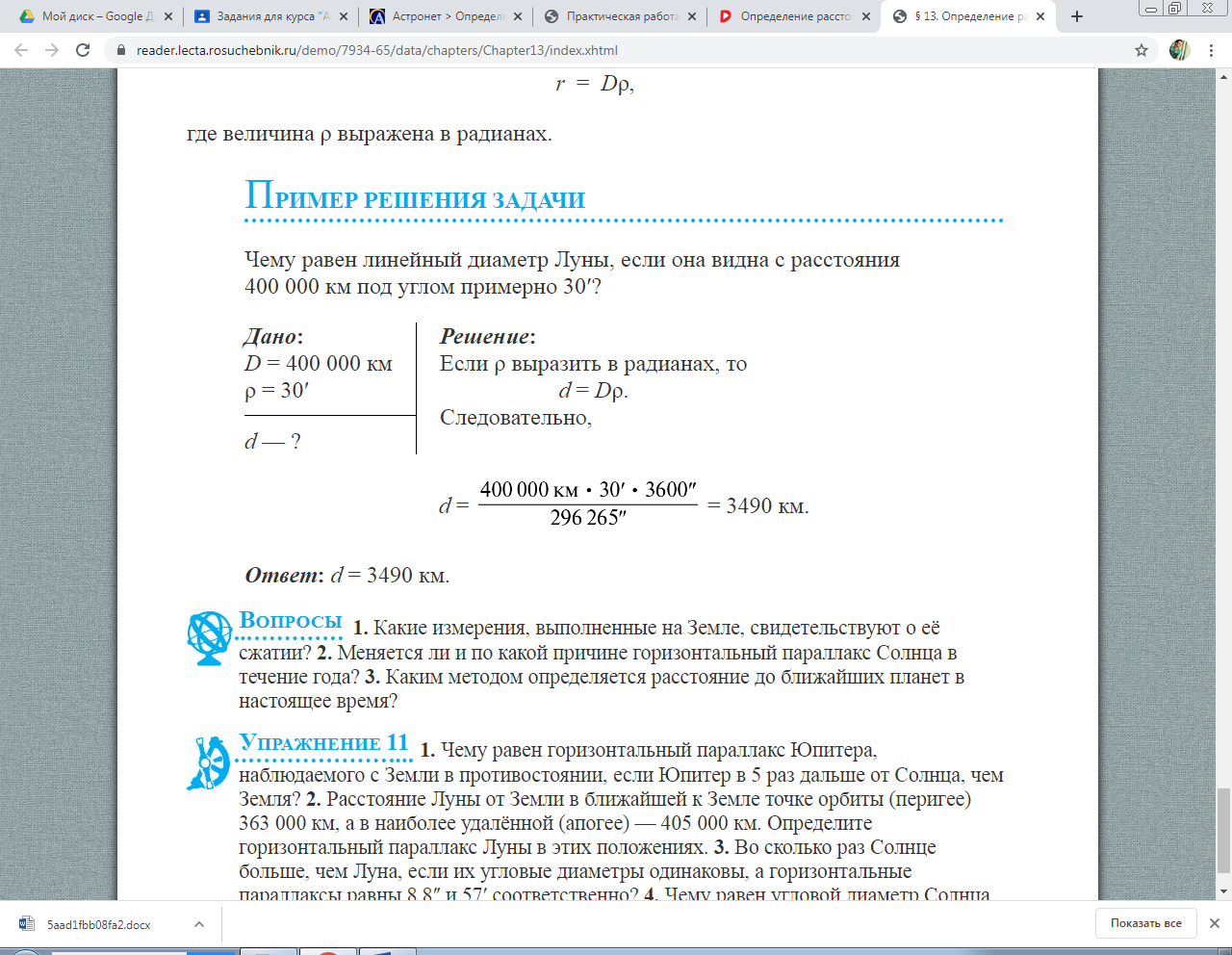 Ответ: d = 3490 км. |
