Лабораторная работа. Лабораторная+определение+теплоты+реакции+окисления. Определение теплоты реакции окисления
 Скачать 1.78 Mb. Скачать 1.78 Mb.
|
|
Лабораторная работа Определение теплоты реакции окисления Цель: Определить теплоту окисления щавелевой кислоты перманганатом калия в кислой среде и проверить степень полноты протекания реакции. Тепловые эффекты реакции (ТЭР) могут быть определены непосредственно при проведении их в калориметре, если они протекают до конца (выделяется газ или выпадает осадок). C2O4H2 ˖2H2O (тв) + 0,4 KMnO4 (р) + 0,6 H2SO4 (р) = 0,2 K2SO4 (р) + 0,4 MnSO4 (р) + 2 CO2 (г) + 3,6 H2O(р) + Q Углекислый газ растворяется в воде и выделяется дополнительная теплота растворения. При интенсивном перемешивании системы и низком парциальном давлении CO2, в воздухе устанавливается равновесие раствора с газовой фазой, которое смещено вправо. Так как энтальпия растворения веществ зависит от концентрации, ТЭР будет зависеть от концентрации реагентов. В работе проводят два опыта: 1) щавелевой кислоты для реакции взято в избытке; 2) в избытке взят KMnO4. В обоих опытах KMnO4 берут одинаковое количество. Ход работы В калориметрический стакан из бюретки влить 34 мл воды, 25 мл H2SO4 (30 %), 16 мл KMnO4 (0,5 н). Поместить в пробирку 0,6 г щавелевой кислоты. Определить ТЭР окисления щавелевой кислоты перманганатом калия. 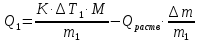 M(COOH)2 ˖ 2 H2O = 126,0625 г/моль; m1 – масса щавелевой кислоты (0,6 г); 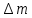 - избыток щавелевой кислоты (0,6 – 0,4 = 0,2 г). - избыток щавелевой кислоты (0,6 – 0,4 = 0,2 г).Теплота растворения щавелевой кислоты 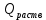 = -35338,3 Дж/моль. = -35338,3 Дж/моль.Взять 34 мл воды, 25 мл H2SO4 (30 %), 16 мл KMnO4 (0,5 н). Поместить в пробирку 0,4 г щавелевой кислоты. Определить ТЭР окисления щавелевой кислоты перманганатом калия. 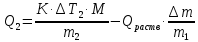 m2 – масса щавелевой кислоты (0,4 г); 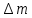 - избыток щавелевой кислоты (0,4 – 0,4 = 0 г). - избыток щавелевой кислоты (0,4 – 0,4 = 0 г).Сопоставить ТЭР обоих опытов и сделать вывод о полноте протекания реакции окисления. Результаты эксперимента О 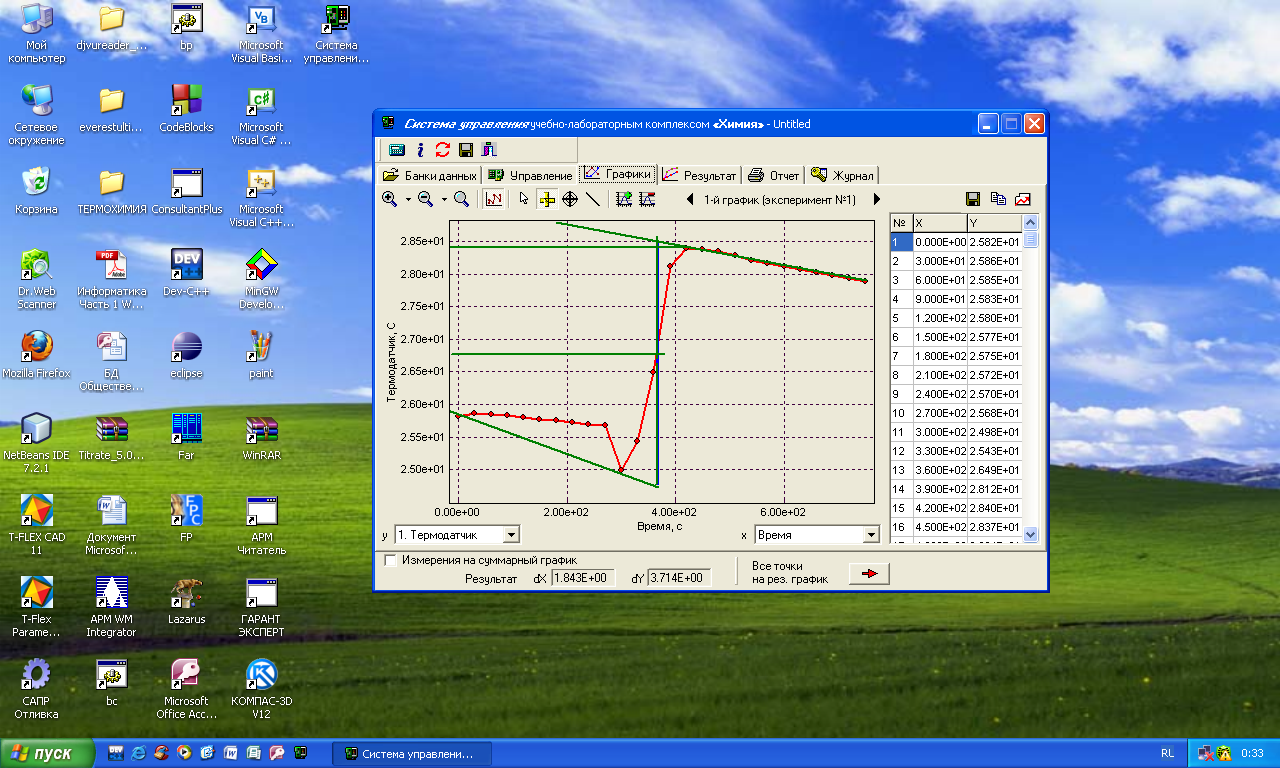 кисление щавелевой кислоты m=0,6 г кисление щавелевой кислоты m=0,6 гОкисление щавелевой кислоты m=0,4 г 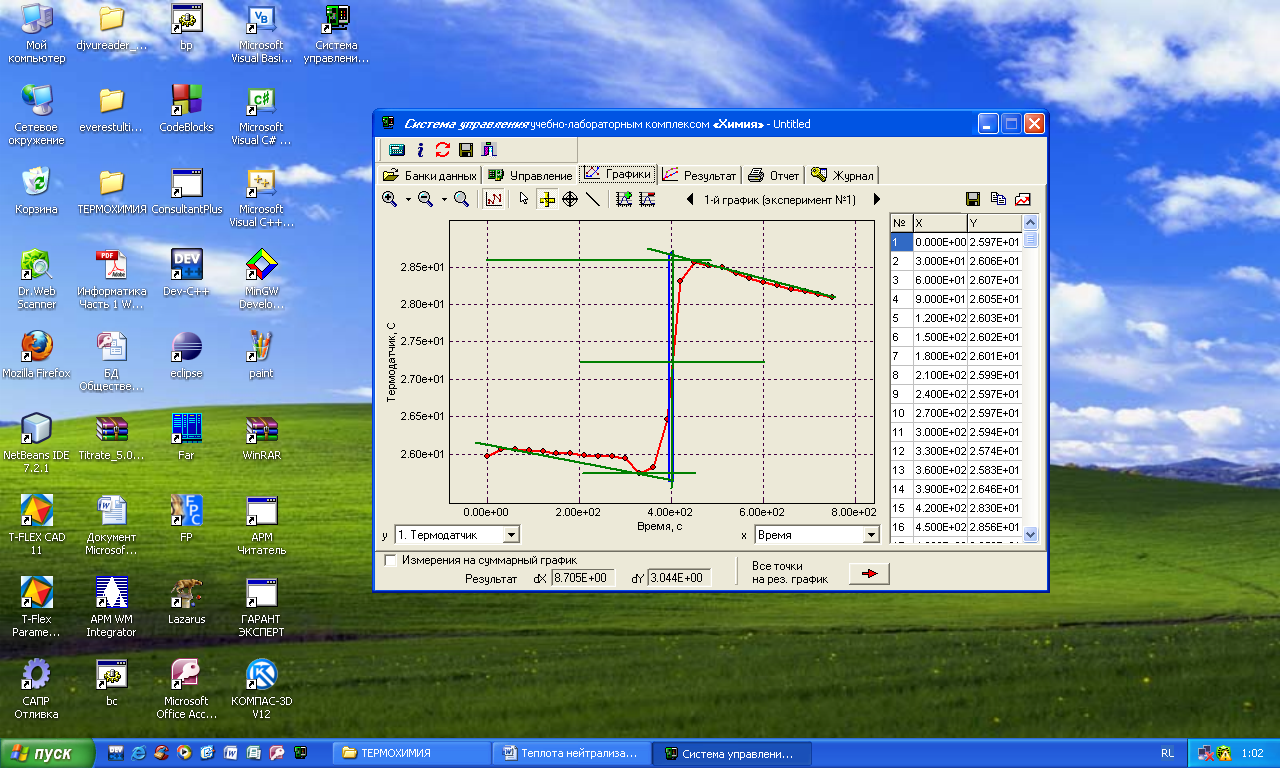 Решение задач Лабораторная работа 5 «Химическое равновесие. Расчёт равновесных концентраций» Многие химические реакции и процессы обратимы. 2NO2 ↔N2O4 (5.1) H2O (ж) ↔ H2O (г) (5.2) CaCO3↔ CaO +CO2 (5.3) Первые два процесса заметно обратимы при обычных условиях, и это можно наблюдать, так как газообразный диоксид азота окрашен в бурый цвет, а газообразный тетраоксид азота безцветен; превращения же жидкой воды в газообразную и наоборот происходят вокруг нас постоянно. Третий процесс заметно обратим при повышенной температуре. Необратимой является, например, реакция разложения дихромата аммония Для обратимых процессов в одних случаях пратические мгновенно, а в других случаях через некоторое время наступает состояние равновесия. В состоянии равновесия концентрации составных частей системы во времени не изменяются. Но равновесия являются динамичными, то есть реакции не прекращаются, поэтому в равновесных процессах, возможны смещения равновесия при внешних воздействиях. В состоянии равновесия между равновесными концентрациями системы устанавливаются постоянные соотношения, количественно характеризующиеся константами равновесия. В выражении константы равновесия в числителе записывается произведение равновесных концентраций (или давлений) компонентов правой части уравнения реакции, а в знаменателе – произведение равновесных концентраций (или) давлений левой части уравнения реакции. Все равновесные концентрации (и давления) записываются в степенях стехиометрических коэффициентов уравнения реакции. В выражениях констант равновесия не отражаются такие компоненты, концентрации которых в процессе реакции не изменяются – это твердые и иногда жидкие вещества. Пример 1. Напишите выражения констант равновесия для вышеприведенных реакций и процессов (5.1) – (5.3). Решение. В соответствии с вышесказанным, выражения константы равновесия можно записать в виде: где 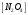 , , 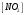 , , 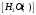 , , 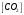 - равновесные концентрации, а - равновесные концентрации, а 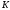 - константа равновесия, зависящая от природы реагирующих веществ и температуры и не зависящая от концентрации. - константа равновесия, зависящая от природы реагирующих веществ и температуры и не зависящая от концентрации. Из примера 1 видно, что равновесная концентрация газообразной воды над жидкой есть величина постоянная (при постоянной температуре). Следует иметь в виду, что концентрация 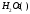 будет оставаться постоянной до тех пор, пока существует равновесие. Если объем над жидкой водой сделать таким большим, что вся вода испариться, то равновесия не будет; в этих условиях концентрация газообразной воды может быть любой величиной, не превышающей равновесную. (Концентрация газообразной воды может превышать равновесную и в отсутсвии жидкой воды, если образуется пересыщенный пар). будет оставаться постоянной до тех пор, пока существует равновесие. Если объем над жидкой водой сделать таким большим, что вся вода испариться, то равновесия не будет; в этих условиях концентрация газообразной воды может быть любой величиной, не превышающей равновесную. (Концентрация газообразной воды может превышать равновесную и в отсутсвии жидкой воды, если образуется пересыщенный пар). Равновесные концентрации системы связаны друг с другом и, как правило, уравнением реакции. Если известны равновесные концентрации, то константы равновесия могут быть рассчитаны. И наоборот, если изветсны константа равновесия и исходные концентрации, то могут быть рассчитаны равновесные концентрации. Пример 2. Вычислите равновесные концентрации водорода и иода, если известно, что их исходные концентрации CH2 и CI2 равны 0,02 моль/л, а равновесная концентрация HI равна 0,03 моль/л. Вычислите константу равновесия. Решение. Из уравнения реакции H2(г) + I2(г)↔2HI(г) видно, что на образование 0,03 моль/л HI расходуется 0,015 моль/л водорода и столько же иода; следовательно,их равновесные концентрации равны и составляют 0,02 – 0,015 = 0,005 моль/л, а константа равновесия Пример 3. В системе CO + Cl2 ↔ COCl2 (при 625 К) [Cl2] = 0,3 моль/л; [CO] = 0,2 моль/л; [COCl2] = 1,2 моль/л. Вычислите константу равновесия системы и начальные концентрации хлора СCl2 и оксида углерода (II) СCO. Решение Константа равновесия Из уравнения реакции видно, что для образования 1,2 моль/л COCl2 расходуется по 1,2 моль/л Cl2и CO. Следовательно, исходная концентрация хлора C Cl2 = 0,3 + 1,2 = 1,5 моль/л, а оксида углерода (II) CCO =0,2 + 1,2 = 1,4 моль/л. Пример 4. Константа равновесия сиситемы H2(г) + I2(г)↔2HI(г) при некоторой температуре равна 40. Определите, сколько процентов водорода и иода перейдет в HI, если исходные концентрации этих веществ составляют CI2 = 0,01 моль/л, CH2 = 0,03 моль/л. Решение. Выразим равновесные концентрации веществ через исходные и уменьшение концентраций водорода и иода к моменту наступления равновесия. Обозначим уменьшение концентрации водорода и иода через x. Следовательно, равновесные концентрации составят 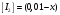 моль/л, моль/л, 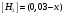 моль/л, моль/л, 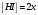 моль/л. моль/л. Для вычисления  подставим числовые значения равновесных концентраций в выражение константы равновесия: подставим числовые значения равновесных концентраций в выражение константы равновесия:Уравнение имеет два корня: 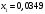 моль/л и моль/л и 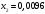 моль/л. По условию начальная концентрация иода равна 0,01 моль/л, значит решением задачи будет моль/л. По условию начальная концентрация иода равна 0,01 моль/л, значит решением задачи будет 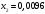 моль/л. моль/л.Таким образом, из 0,01 моль/л иода и 0,03 моль/л водорода прореагировало по 0,0096 моль/л, что составляет соответственно для иода и водорода 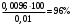 ; ; 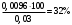 Лабораторная работа №6. Химическое равновесие. Расчет энергии Гиббса и равновесных концентраций Изучение химических реакций в 18 – 19 веках установило, что химические реакции сопровождаются тепловыми эффектами. Многие реакции протекают с выделением теплоты (экзотермические ре-ции), некоторые с поглощением теплоты (эндотермические ре-ции). Датский ученый Х. Томсен в 1954 г. сделал вывод, что количество теплоты, выделившиеся в реакции, является мерой химического сродства. В настоящее время химическое сродство определяют по изменению свободной энергии Гиббса. При этом химическое сродство равно по величине, а по знаку противоположно свободной энергии Гиббса. Стандартая свободная энергия Гиббса и её изменение ∆G0 зависит от изменения энтальпии ∆H0 и изменения энтропии ∆S0 реакции ∆G0 = ∆H0 - T∆S0 Энтропия – это свойство вещества, оказывающее наряду с энтальпией влияние на течение химических процессов. Энтропия обусдавливает возможность существования равновесия. Энтропию выража.т в энтропийных единицах: 1 э.е. = 1 Дж/(моль·К). Изменение энтропии в ходе процесса определяют как разность суммы энтропии продуктов реакции и суммы энтропии исходных веществ. Большие значения энтропии соответствуют более сложным вещесьвам и менее упорядоченным состояниям. Так, энтропия моля СО2 превышает энтропию СО на 16 э.е. При переходе жидкой воды в газообразную энтропия моля воды увеличивается на 118 э.е.. Реакции, сопровождающиеся увеличиением объема газообразных продуктов, характеризуются значительным увеличением энтропии, и наоборот. Пример 1. Вычислите изменение энтропии ΔS0 в реакциях: а) H2S + Cl2 = 2HCl + S(т) б) SO3 (г) = SO2(г) + ½ O2 Решение. Для удобства под формулой каждого вещества напишем значение S0, умноженное на стехиометрический коэфициент уравнения реакции: 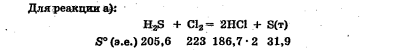 Из суммы энтропий продуктов вычтем сумму энтропий исходных веществ: ΔS0 = (186,7·2 + 31,9) – (205,6 + 223) = -23,3 э.е. Подобным образом для реакции б) Зависимость меджу стандартной свободной энергией Гиббса (ΔG0 ) реакции, измененеием теплосодержания (ΔH0 ) и энтропии (ΔS0 ) ∆G0 = ∆H0 - T∆S0 (5.4) Рассчитать ∆G0 можно двумя способами, пользуясь табличными данными. В первом случае используют свободные энергии Гиббса образования веществ при стандартных условиях. По этим величинам можно расчиать изменение свободной энергии реакции при стандартных условиях, вычитая из суммы стандартных свободных энергий образования продуктов (конечных веществ) сумму стандартных энергий образования исходных веществ. Пример 2. Пользуясь значениями ∆G0 образования отдельных соединений, вычислите ∆G0 реакций: а) COCl2 ↔ CO + Cl2 б) SO2 + NO2 ↔ SO3 + NO определите в каком направлении будут протекать реакции, если все вещества взяты в стандартном состоянии (все вещества газы при 101,3 кПа и 250 С) Решение: а) ΔG0 = (ΔG0 (CO) + ΔG0 (Cl2) – ΔG0 (COCl2) = (-137,2 + 0) + 210,4 = 73,2 кДж/моль. ΔG0>0- следовательно из CO и Cl2 будет образовываться COCl2. б) ΔG0 = (ΔG0 (SO3) + ΔG0 (NO) –[ ΔG0 (SO2) + ΔG0 (NO2) = (-370,4 + 86,6) – (-300,4 + 51,8) -35,2 кДж/моль. Видим, что ΔG0 < 0 – это свидетельствует о том, что будут образовываться SO3 и NO. Второй способ расчета ∆G0 – расчет по энтальпиям образования и энтропиям веществ, значения которыхприведены в справочниках для большинства соединений. Применяя (5.4) и исходя из предположения, что ∆H0 и ∆S0 не зависит от температуры (если в температурном интервале нет фазовых переходов), можно рассчитать ∆G0 при различных температурах. По величине ∆G0 можно судить о том, будут ли вещества расположенные в левой части химического уравнения, превращаться в вещества, указанные в правой. Во-вторых, по величине ∆G0 можно рассчитать константу равновесия К из соотношения: ∆G0 = -RTlnK; K = exp(-∆G0/RT) Описывая реакции с помощью ∆G0, мы описываем равновесные системы. Пример 3 Рассчитайте константы равновесия для реакций а) 2CO + O2 ↔ 2CO2 (при 25 0С) б) COCl2 ↔ CO + Cl2 (при 100 0С) 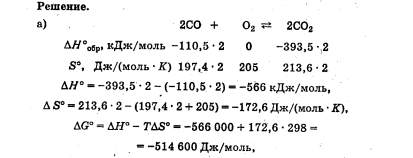 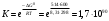 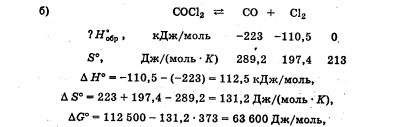 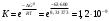 Отрицательной, большой по абсолютной величине свободной энергии соответсвует большая константа равновесия. Большой положительной величине ∆G0 соответствует малая константа равновесия. Константы равновесия могут быть выражены через давления или концентрации, причемв выражении константы равновесия в числителе записываются давления или концентрации продуктов реакции, а в знаменателе – исходных веществ, возведенные в степени стехиометрических коэффициентов.Те компоненты реакции (твердые и иногда жидкие вещества), концентрации которых не могут измениться, в выражения констант равновесия не включают. Константы равновесия выражаются через летучести (для газов) и активности (для растворенных веществ). Летучесть (величина безразмерная) представляет собой отношение давления данного газа к давлению идеального газа при стандартных условиях, то есть к 101,3 кПА. Численно летучесть близка к давлению, измеренному в атмосферах. Активность (величина безразмерная) в первом приближении численно равна конценттрации, выраженной в моль/л. Пример 4. Напишите выражение констант равновесия для следующих химических реакций а) N2 + 3H2 ↔ 2NH3 б)Fe3O4 + 4H2 ↔ 3Fe + 4H2O в) CaCO3 ↔ CaO + CO2 г)CO3 2- +H2O ↔ HCO3 - +OH- Решение Константы равновесия выражаются следующим образом а) 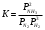 б) 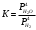 в) 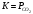 г) 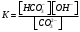 Формулы молекул или ионов, заключенные в квадратные скобки, обозначают равновенсые концентрации. Переход от концентрации газа к далению (атм) можно выполнить по формуле Клайперона-Менделеева n/М – концентрация, моль/м3; n/(1000V) = c –концентрация в моль/л. Тогда p = cRT (Па) и p = cRT/101,3 (атм) Обозначим cRT/101,3 = pT. Отметим, что при Т = 273 К (00С), pT = 24,5 атм, а при Т = 298 К (250С), pT = 24,5 атм – такие давления будут оказывать газы при концентрации 1 М. Тогда можно записать Р = срТ (5.5) Пример 6. Выразите константу равновесия для реакции N2 + 3H2 ↔ 2NH3 Выразите через равновесные концентрации Решение: В константе равновесия, выраженной через давления, заменим давления на концентрации с помощью (5.5): 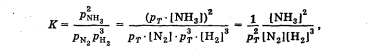 С помощью констант равновесия можно рассчитывать равновесные концентрации в системах. Выражение константы равновесия содержит несколько равновесных концентраций. Поэтому данная математическая задача может быть решена только с помощью составления такого числа дополнительных условий, чтобы число неизвестных не превышало числа уравнений. Дополнительные уравнения составляют на основании уравнения реакций. Однако более просто, а в отношении параллельных реакций и единственно возможно, составлять дополнительные уравнения на основании законов сохранения. Так, химическая реакция – это такая реакция, в которой не изменяется число атомов каждого элемента. Пример 7. Составьте уравнения, отражающие законы сохранения атомов, для реакции N2 + 3H2 ↔ 2NH3 Решение Пусть система задана через начальные исходные концентрации азота 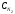 и водорода и водорода 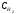 . Введенный в систему азот будет находиться в форме азота N2 и аммика. Составим уравнение относительно числа атомов азота в единицах моль/л. Введено . Введенный в систему азот будет находиться в форме азота N2 и аммика. Составим уравнение относительно числа атомов азота в единицах моль/л. Введено 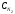 моль/л азота, в нем содержится 2 моль/л азота, в нем содержится 2 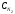 моль/л атомов азота. В системе установится равновесная концентрация непрореагирующего азота [N2 ] моль/л, котоорая будет содержать 2[N2 ] моль/л атомов азота. Образуется [NH3 ] моль/л аммиака, в котором будет содержаться [NH3 ] моль/л атомов азота. Следовательно можно составить равенство моль/л атомов азота. В системе установится равновесная концентрация непрореагирующего азота [N2 ] моль/л, котоорая будет содержать 2[N2 ] моль/л атомов азота. Образуется [NH3 ] моль/л аммиака, в котором будет содержаться [NH3 ] моль/л атомов азота. Следовательно можно составить равенство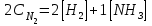 Аналогично составляются уравнение по числу атомов водорода (моль/л): 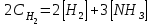 Полученные два уравнения наряду с выражением константы 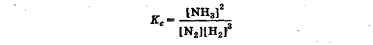 образуют систему из трех уравнений с тремя неизвестными. Пример 8. Рассчитайте равновесные концентрации в системе N2 +3H2↔2NH3 Если исходные концентрации в системе 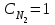 М, М, 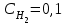 М, температура 25 0С М, температура 25 0СРешение: Рассчитаем ΔG0 и Kc. 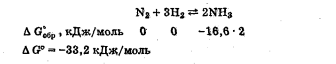 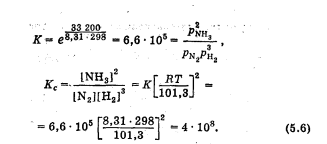 Для облегчения вычислений при решении задач такого типа удобно в качестве искомой неизвестной величины выбрать самую малую – её легче вычислить, а пренебрегая ею в качестве слагаемой и вычитаемой, можно получить более простые уравнения. Судя по величине 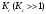 , малая величина находится в знаменателе, а сопоставляя , малая величина находится в знаменателе, а сопоставляя 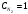 моль/л и моль/л и 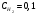 моль/л и уравнение реакции, приходим к выводу, что самой малой равновесной концентрацией будет моль/л и уравнение реакции, приходим к выводу, что самой малой равновесной концентрацией будет 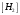 . . Из баланса по числу атомов водорода находим Из баланса по числу атомов азота находим 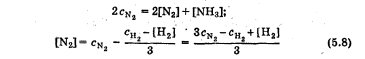 1) Подставим найденные величины в выражение 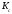 : :Поскольку 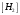 - малая величина, это выражение можно упростить: - малая величина, это выражение можно упростить: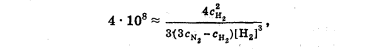 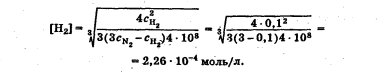 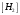 действительно мала по сравнению с действительно мала по сравнению с 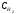 и тем более с и тем более с 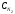 : :Следует иметь в виду, что этот расчет является теоретическим, так как при комнатной температуре из водорода и азота, аммиак не образуется. Эффективный при комнатрной температуре катализатор синтеза аммиака еще не найден. Пример 9. Рассчитайте равновесные концентрации в системе N2 +3H2↔2NH3 При температуре 450 0С, если исходные концентрации равны: А) 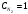 моль/л и моль/л и 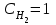 моль/л моль/лБ) 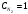 0 моль/л 0 моль/л 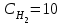 моль/л моль/лРешение. Принимаем, что ∆H0 и ∆S0 реакции не зависит от температуры, рассчитаем ∆G0723 К  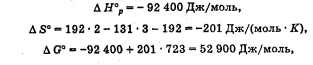 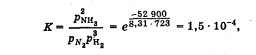 При величине константы, близко к 1, решение задачи без вычислительной техники трудоемко. Решаем задачу с помощью matlab. а) Перепишем уравнение (5.9), КС = 0,53, подставив вместо 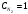 и и 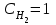 , величины, равные 1 , величины, равные 1 И составим уравнение для решения с помощью Matlab а (ОН-ЛАЙН РЕШЕНИЕ УРАВНЕНИЯ ЧЕТВЁРТОЙ СТЕПЕНИ) Из решения уравнения (5.9б) получаем [H2 ] = 0,568 моль/л. Откуда [NH3] = 0,288 моль/л, [N2] = 0,856 моль/л. б) В формуле (5.9 б) вместо исходных концентраций, равных 1 моль/л, подставляеи 10 моль/л. Получаем новое решение [H2] = 1,95 моль/л; [NH3] = 5,36 моль/л; [N2] = 7,32 моль/л. В общем случае применение свободной энергии Гиббса для описания химических реакций довольно трудоемко. Ориентировочно можно считать, что реакция идет количественно, если 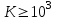 , и практически не идет, если , и практически не идет, если 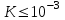 . .При стандартной температуре К > 103 соответствует ∆G0 < -20 кДж/моль и К < 10-3, если ∆G0 > 20 кДж/моль |
