Определитель второго порядка

• Название: Определитель второго порядка
• Дата: 22.11.2022
• Размер: 2.86 Mb.
• Имя файла: kollokvium_po_matematike (1)-1.docx
• Тип: Документы; #804976

1.определитель 2-го и 3-го порядка

Определитель второго порядка равен произведению элементов на главной диагонали минус произведение элементов на побочной диагонали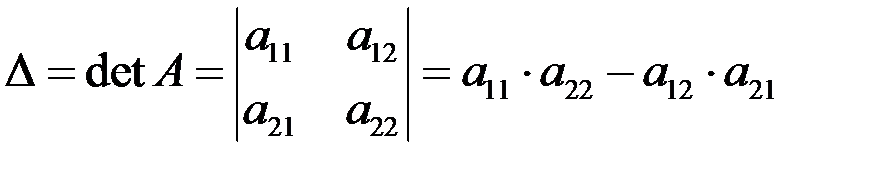

Определителем 3-го порядка, соответствующим матрице А, называется число D, которое определяется выражением: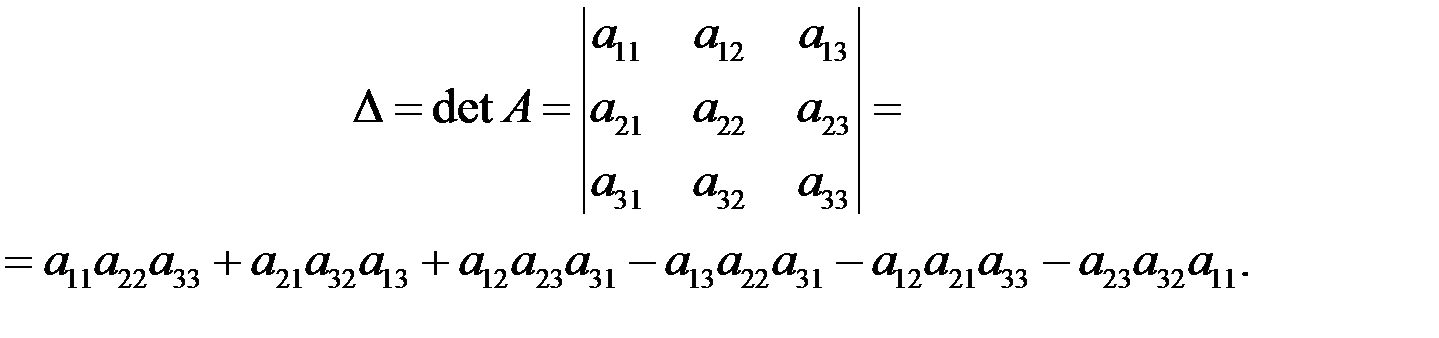



Элементы а₁₁, а₂₂, а₃₃ – расположены на главной диагонали, элементы а₁₃, а₂₂, а₃₁ – на побочной диагонали.

свойства определителей на примере определителя 3-го порядка:

1.Определитель равен сумме произведений элементов какого-нибудь столбца (или строки) на их алгебраические дополнения.

 2. Величина определителя не изменится, если каждую его строку заменить столбцом с тем же номером.

3. Перестановка двух столбцов или двух строк определителя равносильна его умножению на (–1).

4.Общий множитель всех элементов одного столбца или одной строки определителя можно вынести за знак определителя.

5. Если все элементы какой-либо строки или какого-либо столбца равны нулю, то определитель равен нулю.

6. Определитель, имеющий два одинаковых столбца или две одинаковых строки, равен нулю.

7. Определитель равен нулю, если элементы двух столбцов или двух строк пропорциональны.

8. Если каждый элемент некоторой строки (столбца) определителя представлен в виде суммы двух слагаемых, то определитель равен сумме двух определителей, у которых все строки (столбцы), кроме данной, прежние, а в данной строке (столбце) в первом определителе стоят первые слагаемые, а во втором – вторые: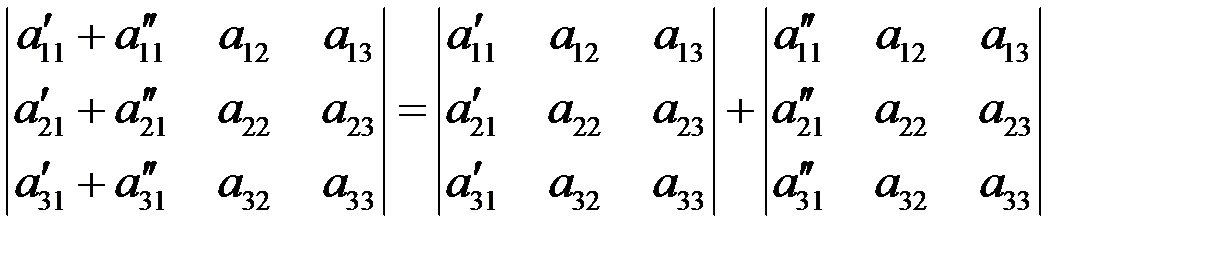

 9.Если к элементам некоторого столбца (или строки) определителя прибавить соответствующие элементы другого столбца (или строки), умноженные на общий множитель, то величина определителя не изменится. 

10. Сумма произведений элементов какого-нибудь столбца (или строки) на алгебраические дополнения элементов другого столбца (или строки) определителя равна нулю.

2.определение n-го порядка. метод вычисления

 Определителем матрицы А (определителем n-го порядка) называется алгебраическая сумма n! слагаемых, каждое из которых есть произведение n элементов матрицы, взятых по одному из каждой строки и каждого столбца. При этом произведение берётся со знаком «+», если подстановка из индексов входящих в него элементов чётная, и со знаком «-» в противном случае.

3.минор и алгебраическое дополнение элемента опредилителя .примеры.

4. матрицы. линейные операции над матрицами. свойства матриц.

Матрицей называется прямоугольная таблица чисел, содержащая m строк одинаковой длины.



Матрицы равны между собой, если равны все их соответствующие элементы.

Матрица, у которой число строк и столбцов равно – называется квадратной.

Матрица, все элементы которой, кроме элементов главной диагонали равны нулю, называется диагональной.

Диагональная матрица, у которой все элементы главной диагонали равны 1, называется единичной. Обозначается буквой Е.

Матрица, у которой все элементы по одну сторону от главной диагонали равны нулю, называется треугольной.

Матрица, у которой все элементы равны нулю, называется нулевой.

1. 
   
   
2. 
   
   
3. 
   
   
4. 
   
   
5. 
   
   
6. 
   
   
7. 
   
   
8. 
   
   

5.произведение двух матриц. переместительный закон умножения. пример умножения матриц 2х2





6.невырожденные матрицы. обратные матрицы.

Невырожденной матрицей называется квадратная матрица   -го порядка, определитель которой отличен от нуля. В противном случае матрица называется вырожденной.



7.ранг матрицы. свойства ранга матрицы



8.системы линейных уравнений. теорема Кронекера-Капелли



9.формула крамера.

(замена толбцов)



10. Решение систем линейных уравнений с помощью матрицы

Методом Гаусса решают системы линейных уравнений с тремя и более неизвестными.

1. 
   Запишите систему уравнений в виде расширенной матрицы. 
   

2. 
   Приведите матрицу к треугольному виду с помощью любых элементарных преобразований: переставляйте строки и столбцы, вычитайте и складывайте строки, умножайте и делите строки на числа (кроме 0), вычеркивайте повторяющиеся и нулевые строки.
   

3. 
   Верните треугольной матрице вид системы уравнений и решите ее обратным ходом, снизу вверх. В нижнем уравнении будет одна неизвестная. Узнайте ее значение и подставьте в предыдущее уравнение. Продолжайте, пока не узнаете значения всех неизвестных.
   

11. Вектор – это направленный отрезок прямой

Коллинеарные вектора

Определение. Вектора, параллельные одной прямой или лежащие на одной прямой называют коллинеарными векторами (рис. 2).

Сонаправленные вектора

Определение. Два коллинеарных вектора a и b называются сонаправленными векторами, если их направления совпадают: a↑↑b (рис. 3).

рис. 3

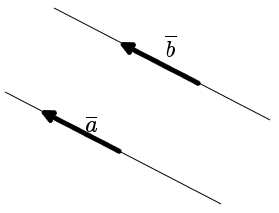
Противоположно направленные вектора

Определение. Два коллинеарных вектора a и b называются противоположно направленными векторами, если их направления противоположны: a↑↓b (рис. 4).

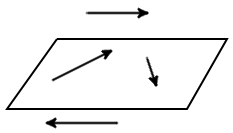
Компланарные вектора

Определение. Вектора, параллельные одной плоскости или лежащие на одной плоскости называют компланарными векторами. (рис. 5).

Всегда возможно найти плоскости параллельную двум произвольным векторам, по этому любые два вектора всегда компланарные.


Равные вектора

Определение. Вектора a и b называются равными, если они лежат на одной или параллельных прямых, их направления совпадают, а длины равны (рис. 6).

рис. 6

То есть, два вектора равны, если они коллинеарные, сонаправленые и имеют равные длины:

a = b, если a↑↑b и |a| = |b|.


Единичный вектор

Определение. Единичным вектором или ортом - называется вектор, длина которого равна единице.

1. Сложение векторов.

а ) Правило треугольника:  . Суммой векторов и называется вектор , идущий из начала первого вектора в конец второго или .

б ) Правило многоугольника  или .
в ) Если векторы образуют замкнутый многоугольник, как показано на рисунке, то сумма векторов равна нулю:
г) Правило параллелограмма: . Под суммой двух векторов
		с общим началом понимается вектор  , выходящий из общего начала и совпадающий по длине и направлению с диагональю параллелограмма, построенного на этих векторах.
2.  Вычитание векторов.
Под разностью векторов  и понимается вектор , который в сумме с вектором  дает вектор , т.е. . Другими словами, это вектор, идущий из конца «вычитаемого» вектора в конец «уменьшаемого» (вторая диагональ параллелограмма),  . Выражение  можно записать иначе . Эту формулу читают так: чтобы из вектора вычесть вектор надо к вектору прибавить вектор противоположный вектору .
3. Умножение вектора на число.
	При умножении вектора на число  длина вектора умножается на это число, а направление не изменяется. При умножении вектора на число длина умножается на число , а направление изменяется на противоположное.

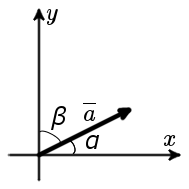
12.

Система ортов (или базисная система векторов) - это система единичных векторов осей координат.

Орт координатной оси Ox обозначается через i¯, оси Oy - через y¯, оси Oz - через k¯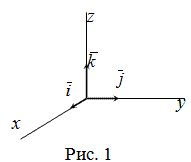 



Для любого вектора a¯=(ax;ay) , который лежит в плоскости xOy, имеет место следующее разложение: a¯=axi¯+ayj¯

Если вектор a¯=(ax;ay;az) расположен в пространстве, то разложение по ортам координатных осей имеет вид: 

Пример

Задание. Зная разложение a¯ по базисной системе векторов: a¯=3i¯−k¯, записать координаты этого вектора в пространстве.

Решение. Коэффициенты при ортах и есть координатами вектора, поэтому из того, что a¯=3i¯−0⋅j¯−k¯, получаем, что a(3.0.-1)

Определение направляющих косинусов

Определение. Направляющие косинусы вектора a – это косинусы углов, которые вектор образует с положительными полуосями координат.

Направляющие косинусы однозначно задают направление вектора.

Основное соотношение. Чтобы найти направляющие косинусы вектора a необходимо соответствующие координаты вектора поделить на модуль вектора.

Соответственно, координаты единичного вектора равны его направляющим косинусам.

Свойство направляющих косинусов. Сумма квадратов направляющих косинусов равна единице.


Формулы вычисления направляющих косинусов вектора

Формула вычисления направляющих косинусов вектора для плоских задач

В случае плоской задачи (рис. 1) направляющие косинусы вектора a = {a_x ; a_y} можно найти воспользовавшись следующей формулой

cos α =	ax	;	cos β =	ay
	|a|			|a|

Свойство:

cos² α + cos² β = 1

рис. 1

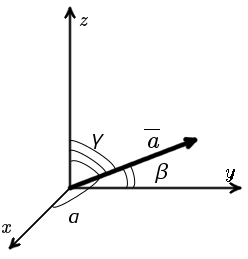
Формула вычисления направляющих косинусов вектора для пространственных задач

В случае пространственной задачи (рис. 2) направляющие косинусы вектора a = {a_x ; a_y ; a_z} можно найти воспользовавшись следующей формулой

cos α =	ax	;	cos β =	ay	;	cos γ =	az
	|a|			|a|			|a|

Свойство:

cos² α + cos² β + cos² γ = 1

рис. 2

Модуль(длинна) вектора |a| = √a_x² + a_y² + a_z²

13. Линейные операции над векторами в координатной форме

Пусть даны два вектора на плоскости: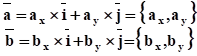



Линейные операции над векторами (сложение, вычитание и умножение вектора на число) в координатной форме выполняются аналитическим способом путем арифметических действий над их одноименными координатами:



1) сложение: ;



2) вычитание: ;



3) умножение вектора на число: , где k-число (скаляр).

Отметим условие коллинеарности векторов в координатной форме.



Если векторы коллинеарны (), то выполняется условие . Тогда

Или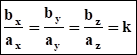



- условие коллинеарности векторов в координатной форме.

Если векторы коллинеарны, то их координаты пропорциональны друг другу.

чтобы найти координаты вектора, надо из координат его конца вычесть координаты начала

14. Скалярное произведение векторов – это произведение их длин на косинус угла между ними. формула скалярного произведения векторов для пространственных задач

В случае пространственной задачи скалярное произведение векторов a = {a_x ; a_y ; a_z} и b = {b_x ; b_y ; b_z} можно найти воспользовавшись следующей формулой:

a · b = a_x · b_x + a_y · b_y + a_z · b_z

Свойства скалярного произведения векторов

1. 
   Скалярное произведение вектора самого на себя всегда больше или равно нуля:
   

a · a ≥ 0

2. 
   Скалярное произведение вектора самого на себя равно нулю тогда и только тогда, когда вектор равен нулевому вектору:
   

a · a = 0   <=>   a = 0

3. 
   Скалярное произведение вектора самого на себя равно квадрату его модуля:
   

a · a = |a|²

4. 
   Операция скалярного умножения коммуникативна:
   

a · b = b · a

5. 
   Если скалярное произведение двух не нулевых векторов равно нулю, то эти вектора ортогональны:
   

a ≠ 0, b ≠ 0, a · b = 0   <=>   a ┴ b

6. 
   (αa) · b = α(a · b)
   
7. 
   Операция скалярного умножения дистрибутивна:
   

(a + b) · c = a · c + b · c

15. Приложения скалярного произведения.

1.) Установление ортогональности векторов.

a * b = 0 => a _I_ b; axbx + ayby + azbz = 0.

2.) Нахождение угла между векторами.

cos(phi) = (a * b) / (|a| * |b|) = (axbx + ayby + azbz) / (sqrt (ax^2 + ay^2 + az^2) * sqrt (bx^2 + by^2 + bz^2))

3.) Нахождение проекции одного вектора на направление другого.

NPb (a) = a * b / |b| = (axbx + ayby + azbz) / (bx^2 + by^2 + bz^2);

NPa(b) = a * b / |a| = (axbx + ayby + azbz) / (ax^2 +by^2 +bz^2);

4.) Нахождение работы постоянной силы.

A = F * S.

16. Векторное произведениие векторов. Площадь параллелограмма,на паре векторов

 Векторным произведением вектора a на вектор b называется вектор c, длина которого численно равна площади параллелограмма построенного на векторах a и b, перпендикулярный к плоскости этих векторов и направленный так, чтоб наименьшее вращение от a к b вокруг вектора c осуществлялось против часовой стрелки, если смотреть с конца вектора c (рис. 1).

рис. 1

Формулы вычисления векторного произведения векторов

Векторное произведение двух векторов a = {a_x; a_y; a_z} и b = {b_x; b_y; b_z} в декартовой системе координат - это вектор, значение которого можно вычислить, используя следующие формулы:

a × b =  ijk a_xa_ya_z b_xb_yb_z

 = i (a_yb_z - a_zb_y) - j (a_xb_z - a_zb_x) + k (a_xb_y - a_yb_x)

a × b = {a_yb_z - a_zb_y; a_zb_x - a_xb_z; a_xb_y - a_yb_x}
Свойства векторного произведения векторов

• 
  Геометрический смысл векторного произведения.
  

 Модуль векторного произведения двух векторов a и b равен площади параллелограмма построенного на этих векторах:

S_парал = [a × b]

• 
  Геометрический смысл векторного произведения.
  

 Площадь треугольника построенного на векторах a и b равна половине модуля векторного произведения этих векторов:

SΔ =	1	|a × b|
	2

• 
  Векторное произведения двух не нулевых векторов a и b равно нулю тогда и только тогда, когда вектора коллинеарны.
  
• 
  Вектор c, равный векторному произведению не нулевых векторов a и b, перпендикулярен этим векторам.
  
• 
  a × b = -b × a
  
• 
  (k a) × b = a × (k b) = k (a × b)
  
• 
  (a + b) × c = a × c + b × c
  

17.Приложение векторного произведения



18.Условие перпендикулярности векторов



19.Условие коллинеарности двух векторов. докаать а*а=0



20.Смешанное произведение векторов. Условие компланарности 3-х векторов

Смешанным (векторно-скалярным) произведением векторов  называется число, определяемое по формуле:  .

 Свойства смешанного произведения:

1.Смешанное произведение не меняется при циклической  перестановке его сомножителей, т.е.  .

2.При перестановке двух соседних сомножителей смешанное произведение меняет свой знак на противоположный, т.е.  .

3.Необходимое и достаточное условие компланарности трех векторов  :  =0.

4.Смешанное произведение трех векторов равно объему параллелепипеда, построенного на этих векторах, взятому со знаком плюс, если эти векторы образуют правую тройку, и со знаком минус, если они образуют левую тройку, т.е.  .

Если известны координаты векторов 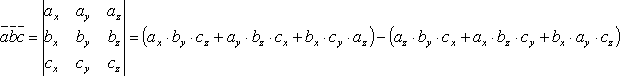 , то смешанное произведение находится по формуле: 

Условие комплонарности 3-х векторов



21.Смешаное произведение. Объем параллелепипеда.