цуа. Оптика. Элементы геометрической и электронной оптики
 Скачать 1.4 Mb. Скачать 1.4 Mb.
|
Формулы Рэлея — Джинса и ПланкаИз рассмотрения законов Стефана — Больцмана и Вина следует, что термодинамический подход к решению задача о нахождении универсальной функции Кирхгофа r,T не дал желаемых результатов. Следующая строгая попытка теоретического вывода зависимости r,T принадлежит английским ученым Д. Рэлею и Д. Джинсу (1877—1946), которые применили к тепловому излучению методы статистической физики, воспользовавшись классическим законом равномерного распределения энергии по степеням свободы. Формула Рэлея — Джинса для спектральной плотности энергетической светимости черного тела имеет вид где =kT— средняя энергия осциллятора с собственной частотой . Для осциллятора, совершающего колебания, средние значения кинетической и потенциальной энергий одинаковы (см. § 50), поэтому средняя энергия каждой колебательной степени свободы =kT. Как показал опыт, выражение (200.1) согласуется с экспериментальными данными только в области достаточно малых частот и больших температур. В области больших частот формула Рэлея — Джинса резко расходится с экспериментом, а также с законом смещения Вина (рис. 288). Кроме того, оказалось, что попытка получить закон Стефана — Больцмана (см. (199.1)) из формулы Рэлея — Джинса приводит к абсурду. Действительно, вычисленная с использованием (200.1) энергетическая светимость черного тела (см. (198.3)) в то время как по закону Стефана — Больцмана Rе пропорциональна четвертой степени температуры. Этот результат получил название «ультрафиолетовой катастрофы». Таким образом, в рамках классической физики не удалось объяснить законы распределения энергии в спектре черного тела.  В области больших частот хорошее согласие с опытом дает формула Вина (закон излучения Вина), полученная им из общих теоретических соображений: где r,T —спектральная плотность энергетической светимости черного тела, С и А — постоянные величины. В современных обозначениях с использованием постоянной Планка, которая в то время еще не была известна, закон излучения Вина может быть записан в виде Правильное, согласующееся с опытными данными выражение для спектральной плотности энергетической светимости черного тела было найдено в 1900 г. немецким физиком М. Планком. Для этого ему пришлось отказаться от установившегося положения классической физики, согласно которому энергия любой системы может изменяться непрерывно, т. е. может принимать любые сколь угодно близкие значения. Согласно выдвинутой Планком квантовой гипотезе, атомные осцилляторы излучают энергию не непрерывно, а определенными порциями — квантами, причем энергия кванта пропорциональна частоте колебания (см. (170.3)): где h= 6,62510–34 Джс — постоянная Планка. Так как излучение испускается порциями, то энергия осциллятора может принимать лишь определенные дискретные значения, кратные целому числу элементарных порций энергии 0: В данном случае среднюю энергию осциллятора нельзя принимать равной kT. В приближении, что распределение осцилляторов по возможным дискретным состояниям подчиняется распределению Больцмана (§ 45), средняя энергия осциллятора а спектральная плотность энергетической светимости черного тела Таким образом, Планк вывел для универсальной функции Кирхгофа формулу которая блестяще согласуется с экспериментальными данными по распределению энергии в спектрах излучения черного тела во всем интервале частот и температур. Теоретический вывод этой формулы М. Планк изложил 14 декабря 1900 г. на заседании Немецкого физического общества. Этот день стал датой рождения квантовой физики. В области малых частот, т. е. при h<<kT (энергия кванта очень мала по сравнению с энергией теплового движения kT), формула Планка (200.3) совпадает с формулой Рэлея — Джинса (200.1). Для доказательства этого разложим экспоненциальную функцию в ряд, ограничившись для рассматриваемого случая двумя первыми членами: Подставляя последнее выражение в формулу Планка (200.3), найдем, что т. е. получили формулу Рэлея — Джинса (200.1). Из формулы Планка можно получить закон Стефана—Больцмана. Согласно (198.3) и (200.3), 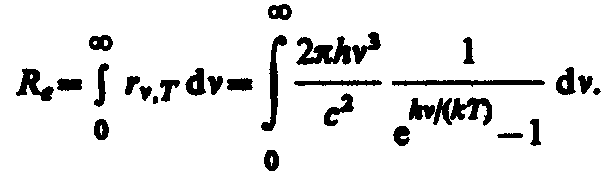 Введем безразмерную переменную x=h/(kt); dx=hd/(kT); d=kTdx/h. Формула для Re преобразуется к виду 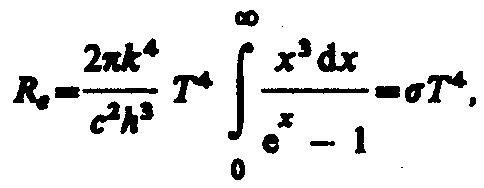 (200.4) (200.4)где 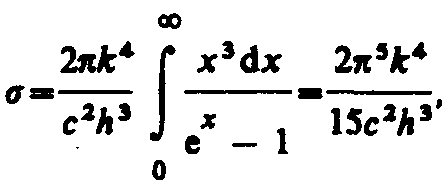 так как так как 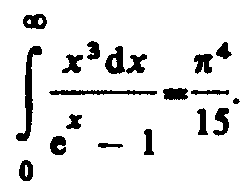 Таким образом, действительно формула Планка позволяет получить закон Стефана — Больцмана (ср. формулы (199.1) и (200.4)). Кроме того, подстановка числовых значений k, с иh дает для постоянной Стефана — Больцмана значение, хорошо согласующееся с экспериментальными данными. Закон смещения Вина получим с помощью формул (197.1) и (200.3): Таким образом, действительно формула Планка позволяет получить закон Стефана — Больцмана (ср. формулы (199.1) и (200.4)). Кроме того, подстановка числовых значений k, с иh дает для постоянной Стефана — Больцмана значение, хорошо согласующееся с экспериментальными данными. Закон смещения Вина получим с помощью формул (197.1) и (200.3):откуда Значение max, при котором функция достигает максимума, найдем, приравняв нулю эту производную. Тогда, введя x=hc/(kTmax), получим уравнение Решение этого трансцендентного уравнения методом последовательных приближений дает x=4,965. Следовательно, hc/(kTmax)=4,965, откуда т. е. получили закон смещения Вина (см. (199.2)). Из формулы Планка, зная универсальные постоянные h, k и с, можно вычислить постоянные Стефана — Больцмана и Вина b. С другой стороны, зная экспериментальные значения и b, можно вычислить значения h и k (именно так и было впервые найдено числовое значение постоянной Планка). Таким образом, формула Планка не только хорошо согласуется с экспериментальными данными, но и содержит в себе частные законы теплового излучения, а также позволяет вычислить постоянные в законах теплового излучения. Следовательно, формула Планка является полным решением основной задачи теплового излучения, поставленной Кирхгофом. Ее решение стало возможным лишь благодаря революционной квантовой гипотезе Планка. |
