Электроника. Организация эвм и систем однопроцессорные эвм

• Название: Организация эвм и систем однопроцессорные эвм
• Анкор: Электроника
• Дата: 14.12.2022
• Размер: 4.17 Mb.
• Имя файла: Book_1.doc
• Тип: Конспект; #845557
• страница: 15 из 18

2.11. Заключительные замечания

Представленный выше материал дает только общее представление о выполнении арифметических операций над двоичными числами в различных системах счисления. Реальные алгоритмы выполнения арифметических операций, используемые в современных ЭВМ, позволяют существенно ускорить процесс вычислений, особенно для операций умножения и деления. Однако эти алгоритмы весьма громоздки и сложны для первоначального понимания. Более полную информацию о них можно найти в литературных источниках, перечисленных ниже.
Библиографический сисок

1. 
   Искусство программирования. Т.1. Основные алгоритмы. 3-е изд., испр. и доп. / Д. Кнут; Под ред. Ю.В. Козаченко М.; СПб.; Киев: ВИЛЬЯМС, 2000. 729 с.
   
2. 
   Искусство программирования. Т.2: Получисленные алгоритмы. 3-е изд., испр. и доп. / Д. Кнут; Под ред. Ю.В. Козаченко М.; СПб.; Киев: ВИЛЬЯМС, 2000. 832с.
   
3. 
   Основы информатики: Учебник для вузов А.Я. Савельев. М.: МГТУ им. М.Э. Баумана, 2001. 328 с.
   
4. 
   Информатика: Системы счисления и компьютерная арифметика:
   / Е.Андреева, И.Фалина; М.: Лаборатория базовых знаний, 1999. 256 с.
   
5. 
   Электронные вычислительные машины и системы: Учеб. пособие для вузов. 3-е изд., перераб. и доп. / Б.М. Каган;М.: Энергоатомиздат, 1991. 592 с.
   
6. 
   Программирование арифметических операций в микропроцессорах: Учеб. пособие для технических вузов. / Злобин В.К., Григорьев В.Л. М.: Высшая школа, 1991. 303 с.
   
7. 
   Микропроцессоры и их применение в системах передачи и обработки сигналов: Учеб. пособие для вузов / Б.А. Калабеков; М.: Радио и связь, 1988. 368 с.
   
8. 
   Введение в микропроцессорную технику / Ч. Гилмор; Под ред. В.М. Кисельникова. М.: Мир, 1984. 334 с.
   

Вопросы для самопроверки

1. 
   Какие виды систем счисления вы знаете?
   
2. 
   В каких случаях целесообразно применять двоичную, восьмеричную и шестнадцатеричную систему счисления?
   
3. 
   Чем двоичная система счисления отличается от двоично-десятичной?
   
4. 
   Как различаются прямой, обратный и дополнительный коды для представления чисел?
   
5. 
   Когда следует применять прямой, обратный и дополнительный коды для представления чисел?
   
6. 
   Что такое переполнение разрядной сетки?
   
7. 
   В каких случаях возникает переполнение разрядной сетки?
   
8. 
   Для чего используют модифицированные коды?
   
9. 
   Опишите алгоритм перевода из дополнительного кода в десятичную систему.
   
10. 
    Поясните понятие «арифметика повышенной точности».
    
11. 
    Опишите формат ЧФЗ.
    
12. 
    Для чего нужны ЧФЗ, почему при работе с ними вводят масштабный коэффициент?
    
13. 
    Опишите формат ЧПЗ.
    
14. 
    В каких случаях используют ЧПЗ? В чем преимущества ЧФЗ и ЧПЗ?
    
15. 
    Что такое нормализация числа?
    
16. 
    Назовите существующие форматы ЧПЗ, используемые в ЭВМ.
    
17. 
    От чего зависит точность представления ЧПЗ в ЭВМ?
    
18. 
    Для чего используется нормализация числа?
    
19. 
    Какие методы ускорения умножения вы знаете? Кратко охарактеризуйте их.
    
20. 
    В каких случаях используется десятичная арифметика?
    
21. 
    Зачем нужна двоично-десятичная коррекция?
    
22. 
    Какие признаки формируются в ЭВМ при нарушении ограничения на длину разрядной сетки?
    
23. 
    Каким образом хранится символьная информация в ЭВМ?
    

Контрольные задания к главе 2

Контрольное задание имеет две формы:

Форма 1 – ответы на теоретические вопросы.

Форма 2 – выполнение арифметических операций.

Выбор формы задания зависит от дополнительных указаний преподавателя.

Форма 1. Ответы на вопросы

1. 
   На листах ответа должны быть указаны номер группы, фамилия студента и номер его варианта.
   
2. 
   Номера вопросов выбираются студентом в соответствии с двумя последними цифрами в его зачетной книжке. В табл. 2.7 а_n-1 – предпоследняя цифра номера, а_n – последняя цифра. В клетках таблицы стоят номера вопросов, на которые необходимо дать письменный ответ
   

Таблица 2.7

an an-1	0	1	2	3	4
0	1,5,9,13,19	2,6,10,14,20	3,7,11,15,21	4,8,12,16,22	1,7,12,17,23
1	3,8,10,18,20	4,6,12,13,22	2,7,9,16,23	1,5,11,14,21	3,6,9,14,19
2	1,6,9,18,19	2,5,10,17,20	1,8,11,16,21	3,5,9,18,22	2,7,9,17,19
3	1,5,9,13,19	2,6,10,14,20	3,7,11,15,21	4,8,12,16,22	1,7,12,17,23
4	3,8,10,18,20	4,6,12,13,22	2,7,9,16,23	1,5,11,14,21	3,6,9,14,19
5	1,6,9,18,19	2,5,10,17,20	1,8,11,16,21	3,5,9,18,22	2,7,9,17,19
6	1,5,9,13,19	2,6,10,14,20	3,7,11,15,21	4,8,12,16,22	1,7,12,17,23
7	3,8,10,18,20	4,6,12,13,22	2,7,9,16,23	1,5,11,14,21	3,6,9,14,19
8	1,6,9,18,19	2,5,10,17,20	1,8,11,16,21	3,5,9,18,22	2,7,9,17,19
9	1,5,9,13,19	2,6,10,14,20	3,7,11,15,21	4,8,12,16,22	1,7,12,17,23

an an-1	5	6	7	8	9
0	2,8,9,15,19	3,5,10,16,20	4,6,11,13,21	1,8,11,17,22	2,5,12,18,23
1	4,7,10,13,20	1,6,12,14,23	2,7,11,15,20	3,5,11,18,21	4,8,10,15,22
2	1,6,10,14,22	3,7,12,16,19	4,7,12,15,23	2,5,10,13,23	4,6,9,17,21
3	2,8,9,15,19	3,5,10,16,20	4,6,11,13,21	1,8,11,17,22	2,5,12,18,23
4	4,7,10,13,20	1,6,12,14,23	2,7,11,15,20	3,5,11,18,21	4,8,10,15,22
5	1,6,10,14,22	3,7,12,16,19	4,7,12,15,23	2,5,10,13,23	4,6,9,17,21
6	2,8,9,15,19	3,5,10,16,20	4,6,11,13,21	1,8,11,17,22	2,5,12,18,23
7	4,7,10,13,20	1,6,12,14,23	2,7,11,15,20	3,5,11,18,21	4,8,10,15,22
8	1,6,10,14,22	3,7,12,16,19	4,7,12,15,23	2,5,10,13,23	4,6,9,17,21
9	2,8,9,15,19	3,5,10,16,20	4,6,11,13,21	1,8,11,17,22	2,5,12,18,23

Форма 2. Выполнение арифметических операций над числами

1. 
   Все действия, производимые над операндами и результатами, включая пере­вод чисел из одной системы счисления в другую, должны быть подробно расписаны в соответствии с алгоритмами, рассмотренными в этом разделе.
   
2. 
   В операциях перемножения указать вариант операции, т.е. "старшими разря­дами вперед" или "младшими разрядами вперед".
   
3. 
   Результаты представить в десятичной системе счисления.
   
4. 
   На листах ответа должны быть указаны номер группы, фамилия студента и номер варианта задания.
   
5. 
   Номер варианта задания выбирается студентом в соответствии с двумя последними цифрами в его зачетной книжке. В табл. 2.8 а_n-1 – предпоследняя цифра номера, а_n – последняя цифра. В клетках табл. 2.8 стоят номера вариантов заданий, полный список которых приведен в табл. 2.9.
   

Таблица 2.8

an an-1	0	1	2	3	4	5	6	7	8	9
0	1	19	34	27	5	14	20	30	9	26
1	28	2	31	4	13	6	15	8	32	10
2	21	35	3	12	22	33	7	16	23	18
3	29	24	11	36	28	25	30	29	17	34
4	20	9	12	8	22	5	15	4	27	1
5	11	36	21	35	14	32	24	33	18	31
6	19	10	13	7	23	6	16	3	26	2
7	17	25	1	15	34	33	27	29	12	20
8	14	2	22	5	35	8	36	9	21	11
9	3	16	4	18	6	19	7	13	10	17

Задание 1. Выполнить арифметические действия, рассматривая операнды как ЧФЗ справа от МЗР в формате 1-го байта. Определить модуль результата. Формат результата – 2 байта.
Задание 2. Выполнить арифметические действия, рассматривая операнды как ЧПЗ с основанием 2 в следующем формате: несмещенный порядок – 4 бита, мантисса – 8 бит. Формат результата – тот же. Округление производить после приведения операнда к нормализованной форме. Результат нормализовать.
Задание 3. Выполнить арифметические действия над операндами, представив их в двоично-десятичном коде.

Варианты заданий Таблица 2.9

№ варианта	Операнды	Задание 1 (ЧФЗ)			Задание 2 (ЧПЗ)			Задание 3 (2-10)
		Операции			Операции			Операции
		X+Y	X-Y	X*Y	X+Y	X-Y	X*Y	X+Y	X-Y	X*Y
1	2	3	4	5	6	7	8	9	10	11
01	X Y	15 33	15 33	15 33	15.33 33.15	15.33 33.15	15.33 33.15	153 331	153 331	153 331
02	X Y	32 67	32 67	32 67	32.67 67.32	32.67 67.32	32.67 67.32	326 673	326 673	326 673
03	X Y	17 37	17 37	17 37	17.37 37.17	17.37 37.17	17.37 37.17	173 371	173 371	173 371
04	X Y	30 63	30 63	30 63	30.63 63.30	30.63 63.30	30.63 63.30	306 633	306 633	306 633
05	X Y	19 41	19 41	19 41	19.41 41.19	19.41 41.19	19.41 41.19	194 411	194 411	194 411
06	X Y	28 59	28 59	28 59	28.59 59.28	28.59 59.28	28.59 59.28	285 592	285 592	285 592
07	X Y	21 45	21 45	21 45	21.45 45.21	21.45 45.21	21.45 45.21	214 452	214 452	214 452
08	X Y	26 55	26 55	26 55	26.55 55.26	26.55 55.26	26.55 55.26	265 552	265 552	265 552
09	X Y	23 49	23 49	23 49	23.49 49.23	23.49 49.23	23.49 49.23	234 492	234 492	234 492

Продолжение табл. 2.9

1	2	3	4	5	6	7	8	9	10	11
10	X Y	24 51	24 51	24 51	24.51 51.24	24.51 51.24	24.51 51.24	245 512	245 512	245 512
11	X Y	25 53	25 53	25 53	25.53 53.25	25.53 53.25	25.53 53.25	255 532	255 532	255 532
12	X Y	22 47	22 47	22 47	22.47 47.22	22.47 47.22	22.47 47.22	224 472	224 472	224 472
13	X Y	27 57	27 57	27 57	27.57 57.27	27.57 57.27	27.57 57.27	275 572	275 572	275 572
14	X Y	20 43	20 43	20 43	20.43 43.20	20.43 43.20	20.43 43.20	204 432	204 432	204 432
15	X Y	29 61	29 61	29 61	29.61 61.29	29.61 61.29	29.61 61.29	296 612	296 612	296 612
16	X Y	38 54	38 54	38 54	38.54 54.38	38.54 54.38	38.54 54.38	385 543	385 543	385 543
17	X Y	31 65	31 65	31 65	31.65 65.31	31.65 65.31	31.65 65.31	316 653	316 653	316 653
18	X Y	16 35	16 35	16 35	16.35 35.16	16.35 35.16	16.35 35.16	163 351	163 351	163 351
19	X Y	13 31	13 31	13 31	13.31 31.13	13.31 31.13	13.31 31.13	133 331	133 331	133 331
20	X Y	18 72	18 72	18 72	18.72 72.18	18.72 72.18	18.72 72.18	187 721	187 721	187 721
21	X Y	15 48	15 48	15 48	15.48 48.15	15.48 48.15	15.48 48.15	154 481	154 481	154 481
22	X Y	41 58	41 58	41 58	41.58 58.41	41.58 58.41	41.58 58.41	415 584	415 584	415 584
23	X Y	22 81	22 81	22 81	22.81 81.22	22.81 81.22	22.81 81.22	228 812	228 812	228 812
24	X Y	19 74	19 74	19 74	19.74 74.19	19.74 74.19	19.74 74.19	197 741	197 741	197 741
25	X Y	46 73	46 73	46 73	46.73 73.46	46.73 73.46	46.73 73.46	467 734	467 734	467 734
26	X Y	38 62	38 62	38 62	38.62 62.38	38.62 62.38	38.62 62.38	386 623	386 623	386 623
27	X Y	14 51	14 51	14 51	14.51 51.14	14.51 51.14	14.51 51.14	145 511	145 511	145 511
28	X Y	23 36	23 36	23 36	23.36 36.23	23.36 36.23	23.36 36.23	233 362	233 362	233 362
29	X Y	34 71	34 71	34 71	34.71 71.34	34.71 71.34	34.71 71.34	347 713	347 713	347 713
30	X Y	19 64	19 64	19 64	19.64 64.19	19.64 64.19	19.64 64.19	196 641	196 641	196 641
31	X Y	42 69	42 69	42 69	42.69 69.42	42.69 69.42	42.69 69.42	426 694	426 694	426 694
32	X Y	35 68	35 68	35 68	35.68 68.35	35.68 68.35	35.68 68.35	356 683	356 683	356 683
33	X Y	21 75	21 75	21 75	21.75 75.21	21.75 75.21	21.75 75.21	217 752	217 752	217 752
34	X Y	17 66	17 66	17 66	17.66 66.17	17.66 66.17	17.66 66.17	176 661	176 661	176 661

Окончание табл. 2.9

35	X Y	35 52	35 52	35 52	35.52 52.35	35.52 52.35	35.52 52.35	355 523	355 523	355 523
36	X Y	28 83	28 83	28 83	28.83 83.28	28.83 83.28	28.83 83.28	288 832	288 832	288 832

Пример выполнения контрольного задания (форма 2)

№ варианта	Операнды	Задание 1 (ЧФЗ)			Задание 2 (ЧПЗ)			Задание 3 (2-10)
		Операции			Операции			Операции
		X+Y	X-Y	X*Y	X+Y	X-Y	X*Y	X+Y	X-Y	X*Y
№	X Y	18 33	18 33	18 33	18.33 33.18	18.33 33.18	18.33 33.18	183 331	183 331	183 331

Задание 1. Выполнить арифметические действия, рассматривая операнды как ЧФЗ справа от МЗР в формате 1-го байта. Определить модуль результата. Формат результата – 2 байта.

1. Выполним операцию сложения Z = X+Y = 18₍₁₀₎ + 33₍₁₀₎ = 51₍₁₀₎.

X = 18₍₁₀₎ = 0001 0010₍₂₎; Y = 33₍₁₀₎ = 0010 0001₍₂₎.

Выполним сложение в ПК: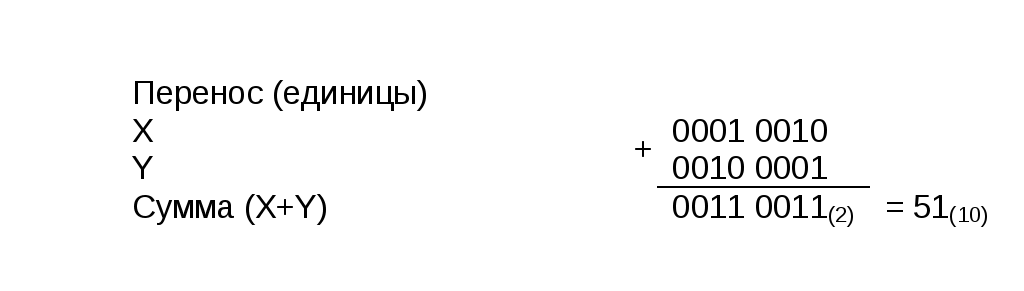


Результат: Z = 0011 0011₍₂₎ = 51₍₁₀₎ .

2. Выполним операцию вычитания Z = X-Y = 18₍₁₀₎ – 33₍₁₀₎ = -15₍₁₀₎.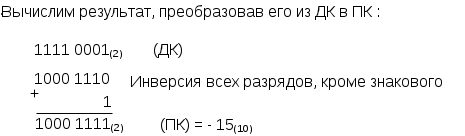


Результат: Z = 1000 1111₍₂₎ = 15₍₁₀₎ .
3. Выполним операцию умножения Z = X*Y = 18₍₁₀₎*33₍₁₀₎ = 594₍₁₀₎.

X = 18₍₁₀₎ = 0001 0010₍₂₎; Y = 33₍₁₀₎ = 0010 0001₍₂₎.

Выполним операцию умножения младшими разрядами вперед: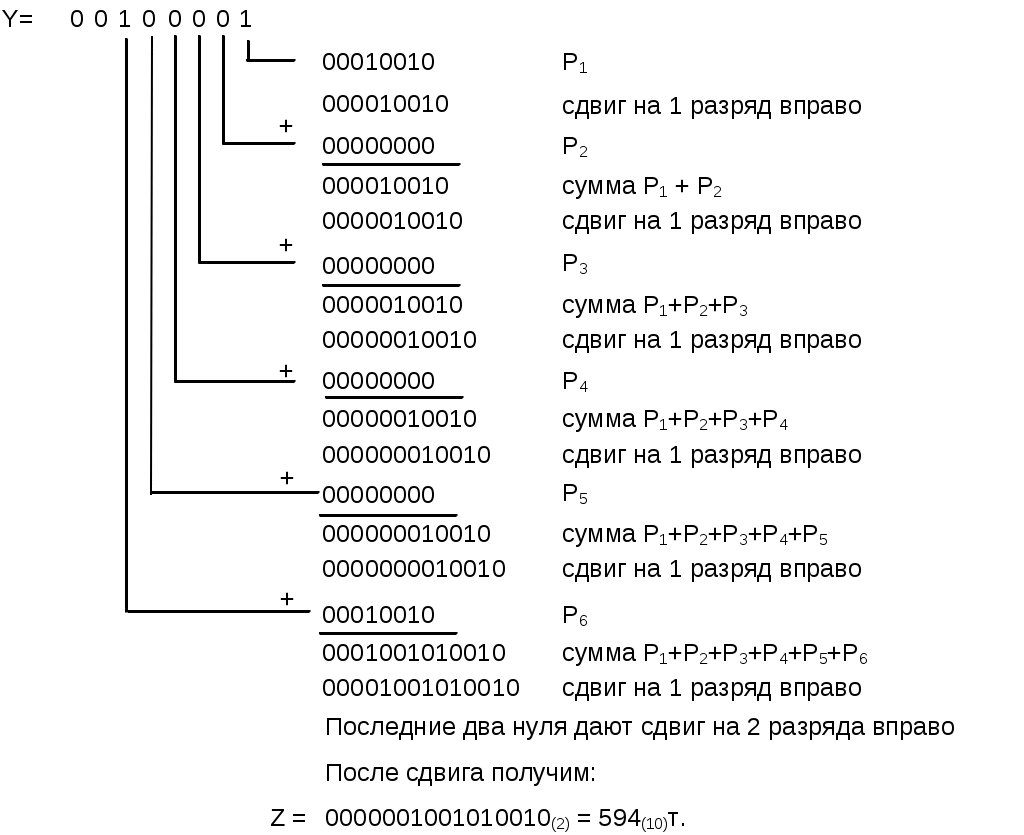

Задание 2. Выполнить арифметические действия, рассматривая операнды как ЧПЗ с основанием 2 в следующем формате: несмещенный порядок – 4 бита, мантисса – 8 бит. Формат результата – тот же. Округление производить после приведения операнда к нормализованной форме. Результат нормализовать.

X = 18.33₍₁₀₎; Y = 33.18₍₁₀₎.

• 
  Преобразуем дробную часть Х, равную 0.33₍₁₀₎, в двоичное число:
  

Таким образом, 0.33₍₁₀₎ = 0.01010100₍₂₎, a X = 18.33₍₁₀₎ = 00010010.01010100₍₂₎.

• 
  Представим X в формате ЧПЗ, округлив значение мантиссы до 8 разрядов (ненормализованное число):
  

• 
  Нормализуем X:
  

• 
  Преобразуем дробную часть Y, равную 0.18₍₁₀₎, в двоичное число:
  

Таким образом, 0.18₍₁₀₎ = 0.00101110₍₂₎, a Y = 33.18₍₁₀₎ = 00100001.00101110₍₂₎.

• 
  Представим Y в формате ЧПЗ, округлив значение мантиссы до 8 разрядов (ненормализованное число):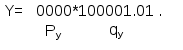
  

• 
  Нормализуем Y: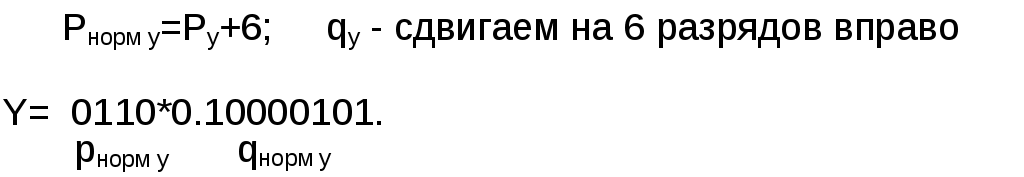
  

1. Выполним операцию сложения Z = X+Y = 18.33₍₁₀₎ + 33.18₍₁₀₎ = 51.51₍₁₀₎.


2. Выполним операцию вычитания Z = X-Y = 18.33₍₁₀₎ + 33.18₍₁₀₎ = -14.85₍₁₀₎.



Результат: Z = (-) 0110 * 0.00111100₍₂₎ = - 2⁶ * 0.234375 = - 15₍₁₀₎

3). Выполним операцию умножения Z = X*Y = 18.33₍₁₀₎*33.18₍₁₀₎ = 608.1894₍₁₀₎.

• 
  Перемножим мантиссы сомножителей (вариант умножения младшими разрядами вперед):
  

• 
  Сложим порядки сомножителей: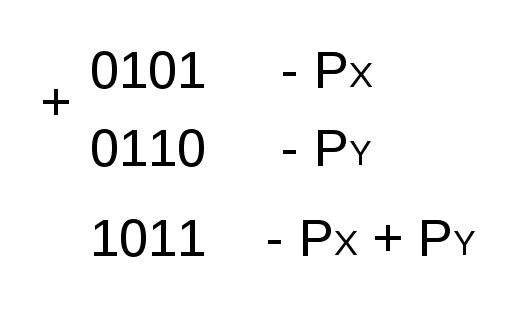
  

• 
  Нормализуем произведение: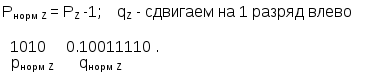
  

Результат: Z = 1010 * 0.10011000₍₂₎ = 2¹⁰ * 0.59375₍₁₀₎ = 608₍₁₀₎.
Задание 3. Выполнить арифметические действия над операндами, представив их в двоично-десятичном коде.
1. Выполним операцию сложения Z=X+Y= 183₍₁₀₎ + 331₍₁₀₎ = 514₍₁₀₎.

X = 183₍₁₀₎ = 0001 1000 0011_(2-10); Y = 331₍₁₀₎ = 0011 0011 0001_(2-10).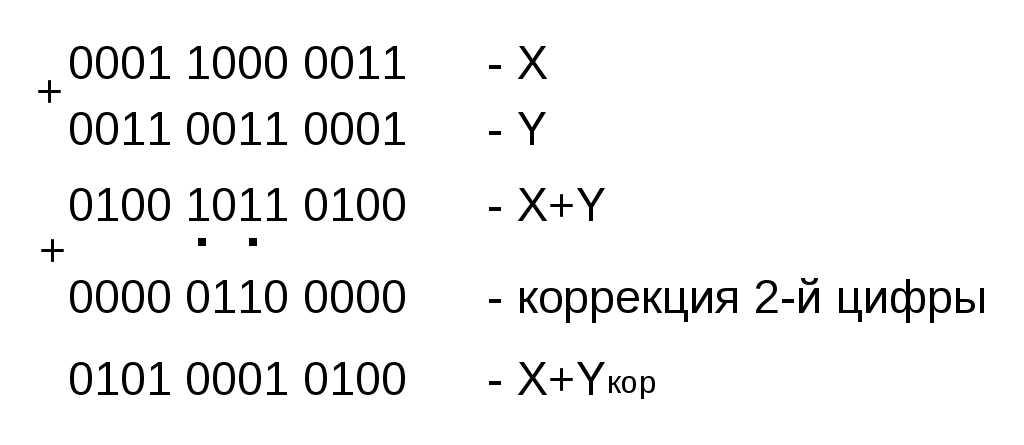


Результат: Z = 0101 0001 0100_(2-10) = 514₍₁₀₎.
2. Выполним операцию вычитания Z = X – Y = 183₍₁₀₎ – 331₍₁₀₎ = -148₍₁₀₎.

• 
  Представим |Y| в ДК с избытком 6: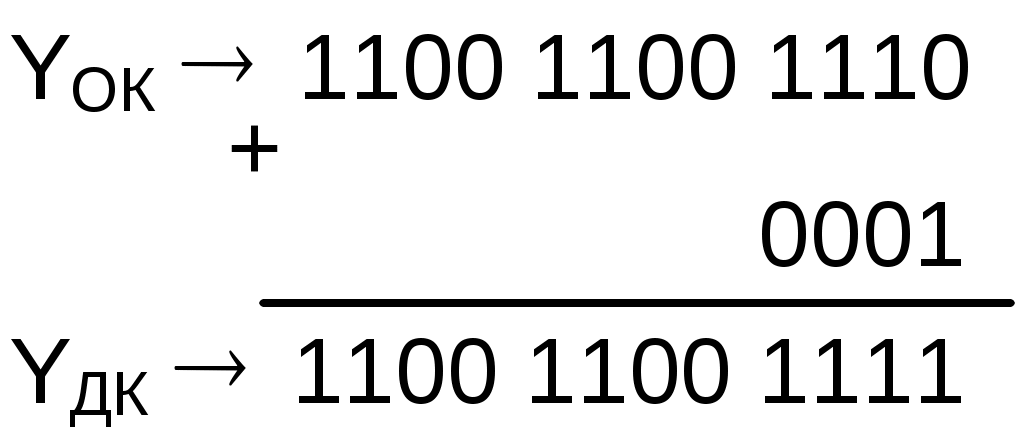
  

• 
  Выполним сложение: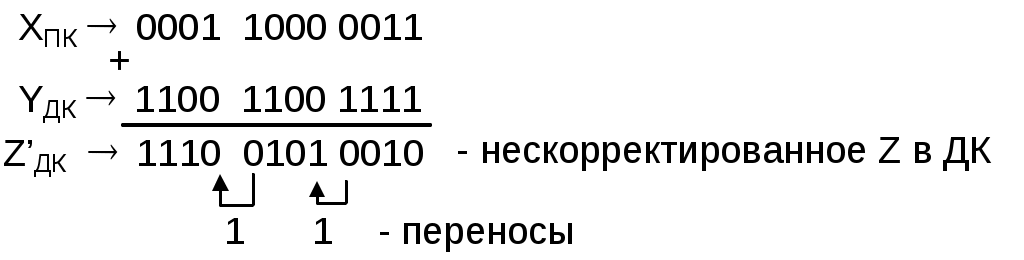
  

Отсутствие переноса из старшей тетрады является признаком того, что результат получился в ДК (т.е. отрицательный).

• 
  Перейдем к нескорректированному избыточному ПК: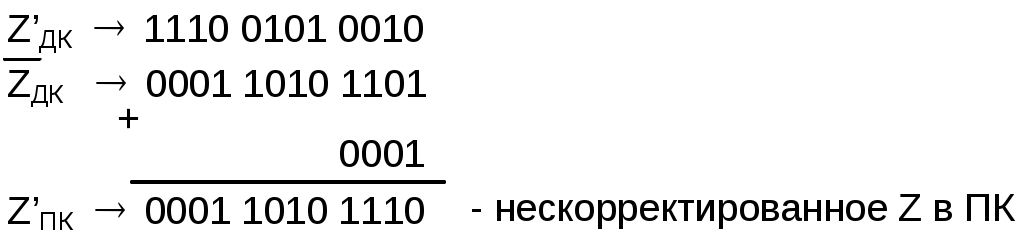
  

• 
  Произведем коррекцию результата в соответствии с п. 5 алгоритма выполнения операции вычитания двоично-десятичных чисел: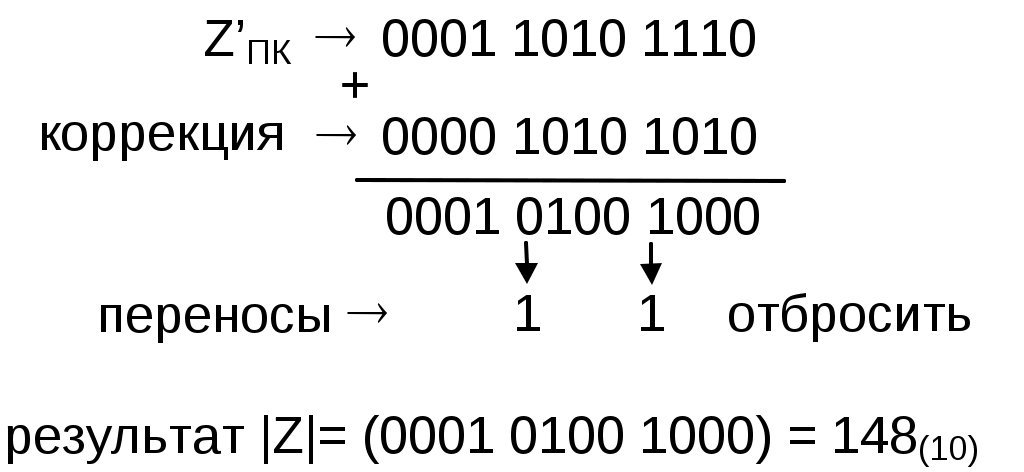
  

Поскольку ранее результат получался в ДК, т.е. отрицательный, необходимо добавить знак (-).
Результат: Z = - ( 0001 0100 1000)_(2-10) = -148₍₁₀₎.
3. Выполним операцию умножения Z = X * Y = 183₍₁₀₎ * 331₍₁₀₎ = 60573₍₁₀₎

X = 183₍₁₀₎ = 0001 1000 0011_(2-10); Y = 331₍₁₀₎ = 0011 0011 0001_(2-10).
Для решения примера выберем вариант перемножения "младшие разряды вперед". В соответствии с п. 1 алгоритма полагаем сумму частичных произведений P₀=0. (Частичные произведения будем обозначать P_i).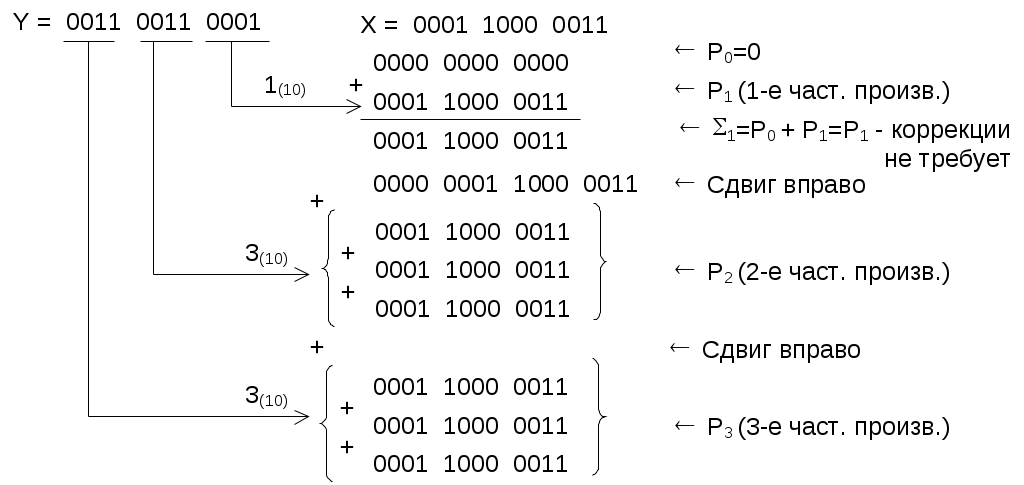

Формирование второго и третьего частичных произведений – более длительная операция, поскольку вторая и третья анализируемые тетрады содержат 3₍₁₀₎, поэтому каждая операция суммирования требует проверки необходимости коррекции. Вычислим P₂ ( P₂ = Р₃ ), последовательно суммируя слагаемые, образующие P₂:


Таким образом, второе (а также и третье) частичное произведение, состоящее из трех слагаемых, имеет вид
P₂ = Р₃ = 0101 0100 1001_(2-10).
Теперь можно вычислить сумму первого, второго и третьего частичного произведений, т.е. результат.

Окончательный результат: Z = 0110 0000 0101 0111 0011_(2-10) = 60573₍₁₀₎.