Организатор Калина (он же жирный хуй)
 Скачать 440.14 Kb. Скачать 440.14 Kb.
|
|
Зачатель: ёбаный Карпухин (он же длинный хуй) Организатор: Калина (он же жирный хуй)Также принимали участие: Смольяков (он же длинный, лысый, жирный Вадим (спортсмен)) Одинцов (он же Ванька) Колупаев (он же волосатый хуй) Филиппов (он же кроссфитёр) Ботов (он же Батон) Гоша (он же волосатый Куценко) Ольга Крупская (она же Соловьёва) p.s. на лечение донатить Кожану (88005553535) 1. Поле. Примеры полей. Поле остатков от деления на p. 2. Линейное пространство над полем. Его простейшие свойства 3. Линейно зависимые и независимые системы векторов. Их свойства. 4. Полные системы векторов. Их свойства. 5. Базис линейного пространства. Единственность разложения по базису. 6. Лемма о замене 7. Лемма Штейница и следствия из нее. Размерность линейного пространства 8. Подпространство линейного пространства. Сумма и пересечение подпространств 9.Линейная оболочка совокупности векторов. 10. Подстановки. Количество инверсий. Транспозиции. Обратная подстановка 11.Операции над матрицами. Ассоциативность произведения матриц 12. Определитель. Неизменность определителя при транспонировании матрицы. Линейность определителя. 13. Перестановка строк (столбцов) определителя. Определитель с двумя одинаковыми строками (столбцами). 14. Разложение определителя по строке (столбцу). 15. Определитель произведения матриц. 16. Элементарные преобразования матриц. Приведение матрицы к ступенчатому виду. 17. Ранг матрицы. Теорема о базисном миноре. 18. Обратная матрица: единственность, условие существования, методы вычисления. 19. Правило Крамера. 20. . Свойства решений однородной системы линейных уравнений. Связь решений однородной системы с решениями неоднородной. 21. Фундаментальная система решений однородной системы 22. Переход к другому базису в линейном пространстве. 23. Линейные операторы. Матрица линейного оператора. Связь координат образа и прообраза. 24. Изменение матрицы линейного оператора при изменении базиса. 25. Алгебра линейных операторов. Её связь с алгеброй матриц 26. Собственные векторы и собственные значения линейного оператора. Характеристическое уравнение. 27. Свойства собственных векторов линейного оператора 28. Условия приведения матрицы к диагональному виду. Жорданова нормальная форма матрицы 29. Евклидовы и унитарные пространства. Неравенство Шварца. Неравенство Коши – Буняковского. 30. Геометрия евклидовых пространств 31. Ортогональный и ортонормированный базисы. Процесс ортогонализации Грама-Шмидта 32. Симметрические (самосопряженные) операторы. Их матрицы. 33. Свойства собственных значений и собственных векторов симметрического оператора. 34. Существование для симметрического оператора ортонормированного базиса из собственный векторов 35. Ортогональные матрицы 36. Ортогональные операторы 37. Линейная и билинейная форма. Их общий вид. 38. Квадратичные формы. Матрица квадратичной формы. Изменение матрицы при изменении базиса. 39. Приведение действительной квадратичной формы к нормальному виду. 40. Положительно и отрицательно определённые квадратичные формы. Критерий Сильвестра. 6. Лемма о замене Пусть L - пространство на полем F, 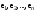 - базис L, - базис L, 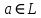 , , 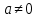 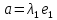 + … + + … + 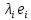 +…+ +…+ 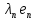 Если 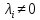 , то его можно заменить на a и получится, что , то его можно заменить на a и получится, что 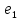 , , 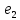 , … , , … , 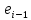 , a, , a, 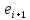 , … , , … , 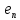 – базис – базисНужно доказать: а) линейную независимость, б) полноту; а) Пусть 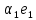 + … + + … + 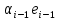 + + 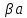 + + 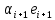 + … + + … + 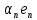 = 0 = 0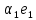 + … + + … + 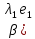 + … + + … + 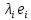 +…+ +…+ 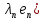 + … + + … + 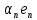 = 0 (подставили a) = 0 (подставили a)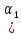 + +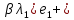 … + … +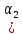 + +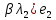 + … + + … +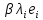 + … + + … + 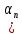 + +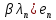 = 0, = 0, где 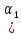 + +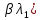 = … = = … = 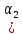 + +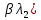 = … = = … = 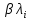 = … = = … = 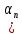 + +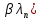 = 0, но = 0, но 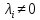 , значит, , значит, 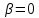 , , значит, 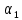 = = 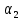 = … = = … = 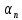 = 0. Следовательно, система линейно независимая. = 0. Следовательно, система линейно независимая.б) Пусть 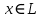 , x = , x = 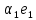 + … + + … + 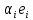 + … + + … + 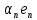 = = 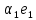 + … + + … + 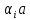 + … + + … + 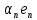 Из разложения а по базису: a = 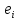 = = 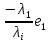 - … + - … + 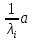 - … - - … - 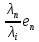 Подставим: x = 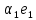 + … + + … + 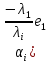 - … + - … + 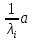 - … - - … - 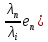 + … + + … + 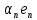 Значит, система полная. 22. Переход к другому базису в линейном пространстве Пусть  - линейное пространство, - линейное пространство, 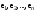 (I)и (I)и 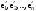 (II) - два базиса в (II) - два базиса в  . .Так как (I) - базис, любой вектор из  , в частности любой вектор системы (II), можно представить в виде линейной комбинации векторов системы (I), т.е. найдутся такие числа , в частности любой вектор системы (II), можно представить в виде линейной комбинации векторов системы (I), т.е. найдутся такие числа 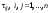 , что , что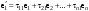 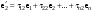 ………………………………. (11.1) 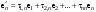 Определение 1. Матрица 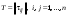 называется матрицей перехода от базиса (I) к базису (II). называется матрицей перехода от базиса (I) к базису (II).Замечание 1. Столбцы матрицы перехода 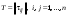 , являются координатами в разложении векторов , являются координатами в разложении векторов 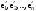 по базису (I). по базису (I).Справедливость этого замечания непосредственно следует из равенств (11.1). Замечание 2.Матрица перехода от базиса к базису является невырожденной матрицей. Доказательство этого факта опустим. Справедливо следующее утверждение. Теорема 1. Пусть  - линейное пространство, - линейное пространство, 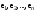 (I) и (I) и 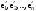 (II) - два базиса в (II) - два базиса в  , ,  - матрица перехода от (I) к (II), - матрица перехода от (I) к (II), 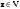 , , 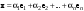 и и 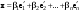 , тогда , тогда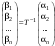 . (11.2) . (11.2)Доказательство. Подставим в разложение  по базису (II) выражения по базису (II) выражения 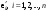 из (11.1), получим из (11.1), получим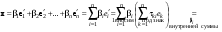 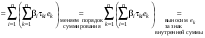 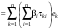 . .Последнюю сумму запишем развернуто: 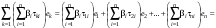 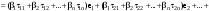 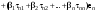 . .По условию 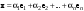 , используя теорему о единственности разложения вектора по базису (теорема 3 в лекции 10), получим , используя теорему о единственности разложения вектора по базису (теорема 3 в лекции 10), получим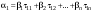 , ,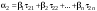 , , …………………………………… 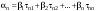 , ,что в матричном виде выглядит как равенство 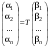 . .Отсюда следует 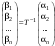 . .Теорема доказана. 23. Линейные операторы. Матрица линейного оператора. Связь координат образа и прообраза. Определение 1. Пусть  - линейное пространство и каждому вектору - линейное пространство и каждому вектору  , принадлежащему , принадлежащему  , поставлен в соответствие вектор , поставлен в соответствие вектор  , , 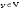 . Соответствие . Соответствие 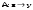 называется оператором, определенным в линейном пространстве называется оператором, определенным в линейном пространстве  . .Принята также запись: 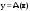 . Вектор . Вектор  называется прообразом, а называется прообразом, а  - образом при отображении оператором - образом при отображении оператором  . .Определение 2. Оператор  , определенный в линейном пространстве , определенный в линейном пространстве  , называется линейным, если: , называется линейным, если:1) 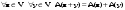 ; ;2) 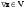 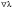 - вещественного числа - вещественного числа 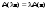 . .Определение 3. Пусть  - линейное пространство, - линейное пространство, 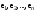 - базис в - базис в  , ,  - линейный оператор в - линейный оператор в  . Матрицей линейного оператора . Матрицей линейного оператора  в базисе в базисе 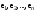 называется матрица называется матрица 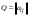 , , 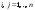 , такая, что , такая, что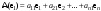 , ,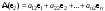 , ,…………………………………….. (12.1) 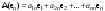 . .Замечание 1. Столбцы матрицы 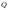 являются координатами в разложении векторов являются координатами в разложении векторов 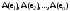 по базису по базису 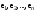 . .Теорема 1. Пусть  - линейное пространство, - линейное пространство, 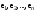 (I) - базис в (I) - базис в  , ,  - линейный оператор в - линейный оператор в  , , 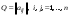 - матрица линейного оператора - матрица линейного оператора  в базисе (I), в базисе (I), 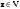 , , 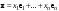 , , 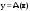 , , 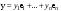 . Тогда . Тогда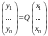 . . Доказательство. Имеем 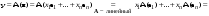 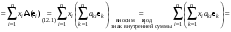 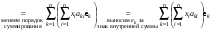 . .По условию 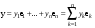 . .Используя теорему о единственности разложения вектора по базису (теорема 3 из лекции 10), получим 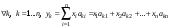 . (12.2) . (12.2)Заметим, что в последнем равенстве числа 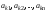 - элементы k-й строки матрицы - элементы k-й строки матрицы 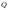 . . Привлекая правило умножения матриц, равенство (12.2) запишем в виде 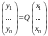 . .Теорема доказана. 24. Изменение матрицы линейного оператора при изменении базиса Пусть линейный оператор ^A: Xn → Xn в базисе e имеет матрицу Ae . Найдем матрицу этого оператора Af в базисе f . Пусть C — матрица перехода от базиса e к базису f . Теорема. Преобразование матрицы оператора ^A при переходе от "старого" базиса e к "новому" базису f определяется формулой:
Доказательство. Рассмотрим произвольный вектор x и его образ y = ^Ax . Обозначим координатные столбцы этих векторов: Xe и Ye — в "старом" базисе e ; Xf и Yf — в "новом" базисе f . Тогда
и
Отсюда, используя формулы преобразования вектора (Пусть системы векторов e = {e1, ..., en} и f = {f1, ..., fn} — два базиса n-мерного линейного пространства Ln. Обозначим xe = (x1,x2, ..., xn) и xf= (x'1,x'2, ..., x'n) — координаты вектора x ∈ Ln соответственно в базисах e и f. Справедливо следующее xe= Ce→f·xf :  Здесь Ce→f — матрица перехода от базиса e к базису f, это матрица, столбцами которой являются координаты базисных векторов f1, ..., fn в базисе e1, ..., en: |
