Организатор Калина (он же жирный хуй)
 Скачать 440.14 Kb. Скачать 440.14 Kb.
|
|
Неравенство Шварца В евклидовом пр-ве (x, y)2 ≤ (x, x)(y,y) Док-во: (x+ λy, x+ λy) ≥0 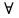 λ λ 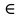 R. R.(x,x) +2λ(x,y) + λ2(y,y) ≥0 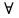 λ λ[ aλ2 + 2bλ + c ≥0 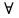 λ D ≤ 0 b2-ac ≤0 ] λ D ≤ 0 b2-ac ≤0 ] (x,y)2 – (x,x)(y,y) ≤0 Нормой вектора х 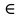 En называется число, равное En называется число, равное 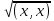 . Обозначим норму ||x||. . Обозначим норму ||x||.Неравенство Коши-Буняковского Для любых 2-х элементов x, y 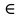 En справедливо: En справедливо:(x,y)2 ≤ ||x|| 2 * ||y|| 2 Док-во: Пусть α – произвольное вещественное число. Положим a = x – αy (a,a) = (x – αy, x – αy) ≥0 f(α) = (x – αy, x – αy) = (x, x) - 2α(x, y) + α2(y, y) ≥0 Т.к 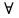 α f(α) ≥0, то дискриминант D квадратного трехчлена f(α) неположителен: α f(α) ≥0, то дискриминант D квадратного трехчлена f(α) неположителен:D = 4(x,y)2 – 4(x,x)(y,y) ≤0 Отсюда (x,y)2 ≤ (x,x)(y,y) или (x,y)2 ≤ ||x|| 2 * ||y|| 2. Теорема доказана 30. Геометрия евклидовых пространств Длиной (нормой) вектора v в евклидовом пространстве 𝔼 называется число 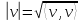 Имея в виду обозначение, длину |v| называют также модулем вектора. Рассматривается арифметическое значение квадратного корня, которое определено для любого вектора из-за неотрицательности подкоренного выражения. Поэтому каждый вектор имеет положительную длину, за исключением нулевого, длина которого равна нулю: |o|=0. Углом между ненулевыми векторами u и v евклидова пространства 𝔼 называется число 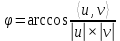 то есть то есть 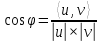 и и 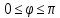 31. Ортогональный и ортонормированный базисы. Процесс ортогонализации Грама-Шмидта. Ортогональные векторы 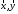 евклидова (или унитарного) пространства – такие, что евклидова (или унитарного) пространства – такие, что 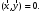 (записывается: (записывается: 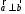 ) )Ортогональная система векторов 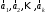 евклидова пространства – такая, что евклидова пространства – такая, что 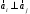 при при 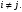 Ортонормированная система векторов – такая система, в которой векторы попарно ортогональны друг другу и длины векторов равны 1: 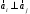 при при 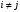 и и 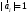 при всех при всех  Базис 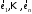 евклидова (или унитарного) пространства называется ортонормированным базисом, если он является ортонормированной системой векторов этого пространства. Аналогичным образом определяется ортогональный базис. евклидова (или унитарного) пространства называется ортонормированным базисом, если он является ортонормированной системой векторов этого пространства. Аналогичным образом определяется ортогональный базис.В любом конечномерном евклидовом или унитарном пространстве существует ортонормированный базис, и для его построения можно использовать процесс ортогонализации. Алгоритм построения ортогонального базиса. Пусть 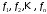 – произвольный базис евклидова пространства. Будем строить по нему ортогональный базис – произвольный базис евклидова пространства. Будем строить по нему ортогональный базис 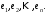 В качестве первого вектора нового базиса возьмём вектор 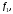 т.е. положим т.е. положим 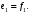 Вектор 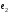 будем искать в виде будем искать в виде 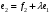 , и подберём , и подберём 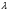 так, чтобы выполнялось условие так, чтобы выполнялось условие 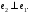 Имеем: Имеем: 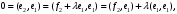 откуда откуда 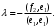 Вектор 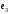 будем искать в виде будем искать в виде 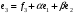 , и подберём , и подберём 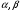 так, чтобы выполнялись условия так, чтобы выполнялись условия 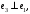 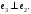 Имеем: Имеем: 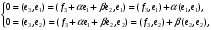 откуда откуда 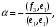 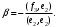 Далее будем искать вектор 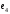 в виде в виде 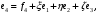 и будем подбирать коэффициенты и будем подбирать коэффициенты 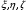 так, чтобы этот вектор был перпендикулярен векторам так, чтобы этот вектор был перпендикулярен векторам 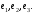 Процесс завершится построением ортогонального базиса 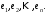 32. Симметрические (самосопряженные) операторы. Их матрицы. 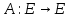 Е-евклидово про-во Е-евклидово про-воА называется симметрическим оператором, если (Ах,у)=(х,Ау) 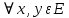 Теорема. Если в Е задать ортонормированный базис е1, ..., еn, то у симметрического оператора матрица будет симметрическая Если матрица некоторого оператора в некотором ортонормированном базисе симметрическая, то оператор симметрический Док-во: А –симметрическая A=AT ; aij = aji 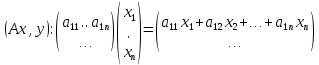 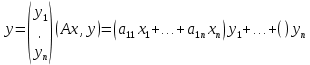 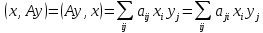 Наоборот, 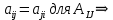 выполняется определение симметрического оператора выполняется определение симметрического оператора33. Свойства собственных значений и собственных векторов симметрического оператора. 1) Все собственные значения действительны Док-во:  Е конечномерно Е конечномерное1, ..., еn – его базис 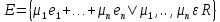 Рассмотрим унитарное про-во: 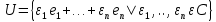 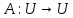 Пусть u - собственный вектор, 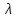 – собственное значение – собственное значение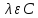 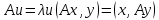 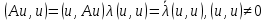 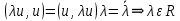 2) Собственные значения с разными 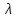 ортогональны друг другу ортогональны друг другу Док-во: 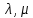 – собственные значения – собственные значения 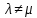 u, v- собственные вектора соотв. собств. значениям 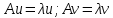 Из 1-ого 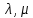 – действительные числа – действительные числа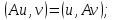 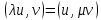 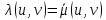 ; ; 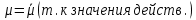 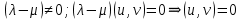 34. Существование для симметрического оператора ортонормированного базиса из собственный векторов 35. Ортогональные матрицы Пусть 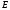 – евклидово пространство. Линейный оператор – евклидово пространство. Линейный оператор 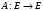 называется ортогональным, если он не изменяет скалярного произведения, т.е. для любых называется ортогональным, если он не изменяет скалярного произведения, т.е. для любых 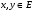 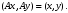 (19) (19)Из определения следует, что ортогональный оператор не изменяет длин векторов и углов между ними, т.е. сохраняет все геометрические свойства фигур. На плоскости или в трёхмерном пространстве ортогональный оператор определяет движение (например, поворот, симметрию относительно прямой, точки, плоскости). Матрицу линейного оператора  будем обозначать так же буквой будем обозначать так же буквой  Для ортогонального оператора имеет место утверждение: Для ортогонального оператора имеет место утверждение:Теорема. Линейный оператор 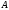 является ортогональным в том и только том случае, если его матрица в ортонормированном базисе удовлетворяет условию является ортогональным в том и только том случае, если его матрица в ортонормированном базисе удовлетворяет условию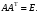 (20) (20) Условие (20) равносильно условию 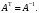 Собственные значения ортогонального оператора по модулю равны 1. Ортогональная матрица – матрица, удовлетворяющая условию (20). У ортогональной матрицы обратная матрица совпадает с транспонированной. Ортогональная матрица – это матрица перехода от одного ортонормированного базиса к другому. 36. Ортогональные операторы Пусть E – евклидово пространство. Линейный оператор A : E → E называется ортогональным, если он не изменяет скалярного произведения, т.е. для любых x, y ϶ E (Ax, Ay) =(x, y). Матрицу линейного оператора A будем обозначать также буквой A. Для ортогонального оператора имеет место утверждение: Теорема. Линейный оператор A является ортогональным в том и только том случае, если его матрица в ортонормированном базисе удовлетворяет условию AT=A-1 37. Линейная и билинейная форма. Их общий вид. L – линейное пространство над полем F. Линейной формой называется отображение α: L →F , удовлетворяющее для всех x, y  L, λ ϶ F следующим условиям:1) α (x+y) =α (x) + α(y); 2) α(λx) =λα (x).линейность L, λ ϶ F следующим условиям:1) α (x+y) =α (x) + α(y); 2) α(λx) =λα (x).линейностьL конечномерно и e1,..,en – его базис. αi=α(ei ) (i=1,...,n). x 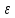 L. x=x1e1+...+ xn en ( x1,.., xn L. x=x1e1+...+ xn en ( x1,.., xn 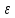 F). F).α(x)= α1x1+...+αnxn. канонический вид Отображение B : LxL → F называется билинейной формой, если оно для всех x, y, z 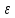 L и λ L и λ 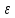 F удовлетворяет условиям: F удовлетворяет условиям:1) B(x+y, z) =B(x, z) +B(y, z); 2) B(λx, y) =λB(x, y); 3) B(x, y +z) =B(x,y)+B(x, z); 4) B(x,λ y) =λB(x, y). в пространстве L есть конечный базис e1,…,en. Если обозначить bij=B(ei,ej ), то для любых векторов x, y 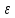 L мы будем иметь: L мы будем иметь: 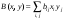 n2 слагаемых n2 слагаемых38. Квадратичные формы. Матрица квадратичной формы. Изменение матрицы при изменении базиса. 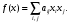 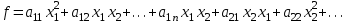 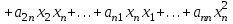 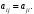 матрица квадратичной формы – симметрическая.(A=AT) матрица квадратичной формы – симметрическая.(A=AT)Изменение матрицы при переходе в др. базис: A1=STAS S=Te→e1 Д-во: 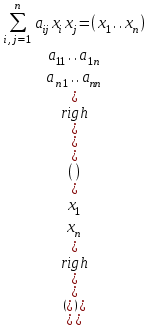 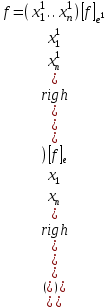 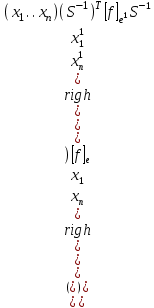 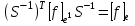 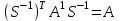 39. Приведение действительной квадратичной формы к нормальному виду. Определение. Нормальным видом квадратичной формы называется сумма квадратов неизвестных с коэффициентами «+1» или « 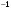 ». ».Теорема. Всякую квадратичную форму можно привести некоторым невырожденным линейным преобразованием неизвестных к нормальному виду. Доказательство. Пусть 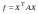 - квадратичная форма ранга - квадратичная форма ранга  . Следовательно, . Следовательно, 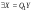 - линейное преобразование неизвестных, приводящее - линейное преобразование неизвестных, приводящее 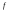 к виду к виду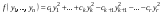 , (14.20) , (14.20)где 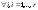 , , 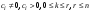 (теорема 3 и следствие из теоремы 2). (теорема 3 и следствие из теоремы 2). Положим 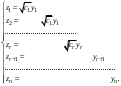 (14.21) (14.21)Равенства (14.21) можно записать в виде следующего матричного равенства:  , ,где 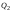 - невырожденная матрица (так как - невырожденная матрица (так как 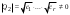 ), следовательно, существует ), следовательно, существует 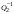 и равенство и равенство 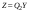 можно разрешить относительно можно разрешить относительно  : : 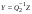 . .Последовательное выполнение линейных преобразований 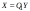 и и 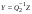 является линейным преобразованием с матрицей является линейным преобразованием с матрицей 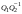 (теорема 1); линейное преобразование (теорема 1); линейное преобразование 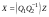 приводит квадратичную форму приводит квадратичную форму 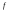 к нормальному виду к нормальному виду . .Теорема доказана. 40. Положительно и отрицательно определённые квадратичные формы. Критерий Сильвестра. Определение. Квадратичная функция  на линейном пространстве L называется положительно определенной, если на линейном пространстве L называется положительно определенной, если  ; ; Пусть в некотором базисе квадратичная функция записана в виде квадратичной формы 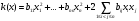 (1) (1)с матрицей 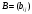 |
