Организатор Калина (он же жирный хуй)
 Скачать 440.14 Kb. Скачать 440.14 Kb.
|
|
f1 = с11· e2 + с21· e1 + ... + сn1· en, f2 = с12· e1 + с22· e2 + ... + сn2· en, ..., fn = с1n· e2 + ... + сnn· en. Формулу преобразования координат вектора при изменении базиса принято записывать в виде xf= (Ce→f)− 1·xe), получаем
Сравнивая с выражением Yf = Af · Xf , приходим к формуле (1), которую требовалось доказать. 25. Алгебра линейных операторов. Её связь с алгеброй матриц. Алгеброй называется множество, которое является пространством над полем F, где определено умножение ab Первые 8 аксиом линейного пространства действуют. 9) (a+b)c = ac+bc 10) aλb=λab=λab 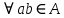 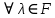 A, B : L -> L (A+B)x = Ax + Bx (A+B)(x+y)=(A+B)x + (A+B)y = Ax + Ay + Bx + By = (A+B)x + (A+B)y (AB)x = A(Bx) AB(x+y)=A(B(x+y))=A(Bx+By)=(AB)x+(AB)y=(AB)(x+y) (AB) α (x) = A(B(αx)) = (Bαx) A = αA(Bx) = α (ABx) 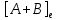 = =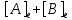 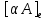 = α = α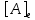 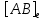 = =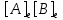 26. Собственные векторы и собственные значения линейного оператора. Характеристическое уравнение. Определение 4. Квадратные матрицы  и и  называются подобными, если существует невырожденная матрица называются подобными, если существует невырожденная матрица 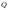 , такая, что , такая, что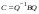 . .Теорема 2. Пусть  - линейное пространство, - линейное пространство, 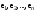 (I) и (I) и 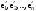 (II) - два базиса в (II) - два базиса в  , ,  - матрица перехода от (I) к (II), - матрица перехода от (I) к (II),  - линейный оператор в - линейный оператор в  , ,  - матрица оператора - матрица оператора  в (I), в (I),  - матрица оператора - матрица оператора  в (II). Тогда в (II). Тогда 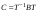 . .Это утверждение примем без доказательства. Пусть 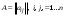 . Матрица . Матрица 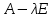 , где , где  - единичная матрица порядка - единичная матрица порядка  , а , а  - произвольное вещественное число, называется характеристической матрицей для - произвольное вещественное число, называется характеристической матрицей для  . Она имеет вид . Она имеет вид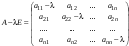 . .Определитель 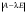 - некоторый многочлен порядка - некоторый многочлен порядка  относительно относительно  . . Определение 5. Многочлен 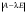 называется характеристическим многочленом матрицы называется характеристическим многочленом матрицы  , а его корни - характеристическими корнями матрицы , а его корни - характеристическими корнями матрицы  . .Теорема 3. Подобные матрицы имеют одинаковый набор характеристических корней. Доказательство. Пусть 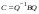 , , 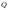 - невырожденная матрица. Имеем - невырожденная матрица. Имеем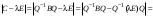 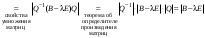 . .Характеристические многочлены матриц В и С совпадают, следовательно, совпадают и характеристические корни. Теорема доказана. Следствие. Матрицы, задающие линейный оператор в различных базисах, имеют один набор характеристических корней (теорема 2 + теорема 3). Определение 6. Характеристические корни матрицы линейного оператора (в любом базисе) называются характеристическими корнями линейного оператора. Определение 7. Весь набор характеристических корней называется спектром оператора. Определение 8. Пусть  - линейное пространство, - линейное пространство,  - линейный оператор в - линейный оператор в  . Вектор . Вектор 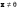 называется собственным вектором оператора называется собственным вектором оператора  , если найдется действительное число , если найдется действительное число  такое, что такое, что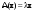 . .Число  называется собственным значением, соответствующим данному собственному вектору называется собственным значением, соответствующим данному собственному вектору  . .Справедливо следующее утверждение, которое приведем без доказательства. Теорема 4. Действительные характеристические корни линейного оператора, если они существуют, и только они, служат собственными значениями линейного оператора. Характеристическое уравнение в математике, 1) Х. у. матрицы — алгебраическое уравнение вида 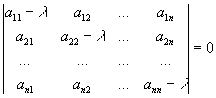 ; ;Матрицу {\displaystyle A-\lambda E}  . .Уравнение  . .27. Свойства собственных векторов линейного оператора Теорема. Пусть собственные значения 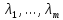 оператора различны. Тогда отвечающие им собственные векторы линейно независимы. оператора различны. Тогда отвечающие им собственные векторы линейно независимы.Доказательство проведем методом математической индукции по количеству векторов. Для одного собственного вектора утверждение теоремы очевидно. Предположим, что утверждение теоремы верно для m-1 векторов 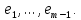 Добавим к этим векторам еще один вектор Добавим к этим векторам еще один вектор 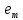 . Предположим, что эта система из m векторов линейно зависима, т.е. существуют числа . Предположим, что эта система из m векторов линейно зависима, т.е. существуют числа 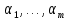 , одновременно не равные нулю, такие, что , одновременно не равные нулю, такие, что 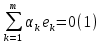 Применим к обеим частям равенства оператор: 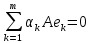 Так как векторы 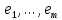 - собственные, отвечающие различным собственным значениям - собственные, отвечающие различным собственным значениям 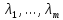 , то: , то: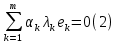 Вычтем из равенства равенство, умноженное на 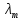 : :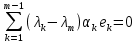 Так как все числа 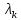 различны, то из линейной независимости векторов различны, то из линейной независимости векторов 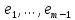 следует равенство нулю коэффициентов следует равенство нулю коэффициентов 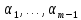 . Но тогда из равенства (1) следует, что . Но тогда из равенства (1) следует, что 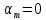 . Это означает, что векторы . Это означает, что векторы 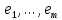 линейно независимы. линейно независимы. Теорема доказана. Следствие. Если характеристический многочлен линейного оператора имеет nразличных корней, то существует базис, в котором матрица этого оператора имеет диагональный вид. Действительно, если характеристический многочлен оператора имеет ровно n различных корней, то оператор имеет n различных собственных значений. Этим собственным значениям соответствуют n собственных векторов, причем они линейно независимы. Возьмем их в качестве базисных. Очевидно, в таком базисе матрица оператора будет диагональной, и на диагонали будут стоять собственные значения оператора. 28. Условия приведения матрицы к диагональному виду. Жорданова нормальная форма матрицы Определение: Матрица приводится к диагональному виду, если существует базис в котором матрица этого оператора диагональная. А-матрица n*n над полем F, матрица линейного оператора D= 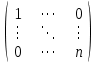 Существует ли такой переход S, что S-1AS=D? Диагональная ли D? Если да, то матрица А приводится, если нет, то А-не приводится Пусть А-приводится к диагональному виду, т.е. S S-1AS=D A = SDS-1; A2=SDS-1SDS-1 = SD2S-1 A3 = SDS-1SDS-1SDS-1 = SD3S-1 Ak = SDkS-1 (S-1BS)m = S-1BmS Теорема: матрица приводится к диагональному виду базис из собственных векторов и на диагонали собственные числа Доказательство: 1)Дано: А-приводится к диаг. виду. Д-ть: базиса из собственных векторов S-1AS=D S - невырожденная матрица перехода: S= 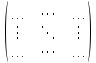 e1’ e2’ en’ D=[A]e’= 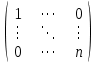 Ae1’=1e1’+0e2’+…+0en’ Ae1’=1e1’+0e2’+…+0en’Ae1’=1e1’ – собственный вектор, 1 – собственное значение Ae2’=2e2’ – собственный вектор, 2 – собственное значение базис из собственных векторов 2) Дано: базиса из собственных. Д-ть: матрица приводится к диаг. виду. e1, e2, …, en – исходный базис собственных векторов u1,u2,…, un – новый базис собственных векторов S=Teu [A]u= 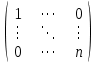 Au1=1u1=1u1+0u2+…+0un Au1=1u1=1u1+0u2+…+0unAu1 Aun Au2=2u2=0u1+2u2+…+0un и т.д. [A]u - диагональная [A]u = S-1AS существует Достаточность условия приведения приводимости к диагональному виду: Если корни характеристического уравнения 1, …, n различны U1, U2, …, Un собственные векторы. Знаем: U1, U2, …, Un – линейно независимы U1, U2, …, Un – базис Если матрица симметрическая (т.е. AT=A), то приводится (для поля R) 29. Евклидовы и унитарные пространства. Неравенство Шварца. Неравенство Коши – Буняковского. Линейное пр-во E над полем R называется Евклидовым, если определено умножение (x,y) 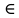 R, x,y R, x,y 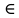 Е и оно удовлетворяет: Е и оно удовлетворяет:(х,х)≥0, если (х,х)=0 x=0. Линейность (x+y,z)=(x,z)+(y,z) (λx,y)= λ(x,y) λ 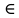 R R(y,x)=(x,y) (x,y) – скалярное произведение В 3-х мерном линейном пространстве (x,y) = |x|*|y|*cos( 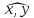 ) )Унитарное пр-во – линейное пр-во над полем C в котором есть скалярное произведение (компланарное число) и: (х,х)≥0, если (х,х)=0 x=0. (x+y,z) = (x,z)+(y,z) (λ x,y) = λ(x,y) λ 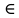 R R(y,x) = 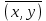 (x, λy) = 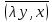 = = 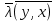 = λ(x,y) = λ(x,y)(x,y) = x*y = x1y1 + x2y2 + … + xnyn ,поэтому (x,0)=0 |
