Основы технологии машиностроения комплекс учебнометодических материалов
 Скачать 1.21 Mb. Скачать 1.21 Mb.
|
|
Результаты измерений партии деталей
На основании данных измерений строим статистические оценки распределения размеров: гистограмму и полигон распределения (рис. 74). Ступенчатая линия характеризует гистограмму распределения; ломаная линия, соединяющая точки, соответствующие середине каждого интервала, характеризует полигон распределения размеров. При большом числе замеряемых деталей и большом количестве интервалов размеров ломаная линия приближается к плавной кривой – кривой распределения размеров.  Рис. 74. Гистограмма и полигон распределения размеров Для построения гистограммы рекомендуется измеренные размеры разбивать не менее чем на шесть интервалов, при этом общее число замеряемых деталей должно быть не менее 100. Чем больше число замеряемых деталей, тем точнее получаем полное распределение размеров. Как показывает практика, в технологии машиностроения в зависимости от условий обработки рассеивание величин погрешностей подчиняется различным распределениям, известным из математической статистики. Наибольшее практическое применение получили закон нормального распределения – закон Гаусса, закон Максвелла, закон модуля разности, закон равной вероятности. Многочисленными исследованиями установлено, что распределение размеров деталей, обработанных на настроенном станке, подчиняется нормальному распределению 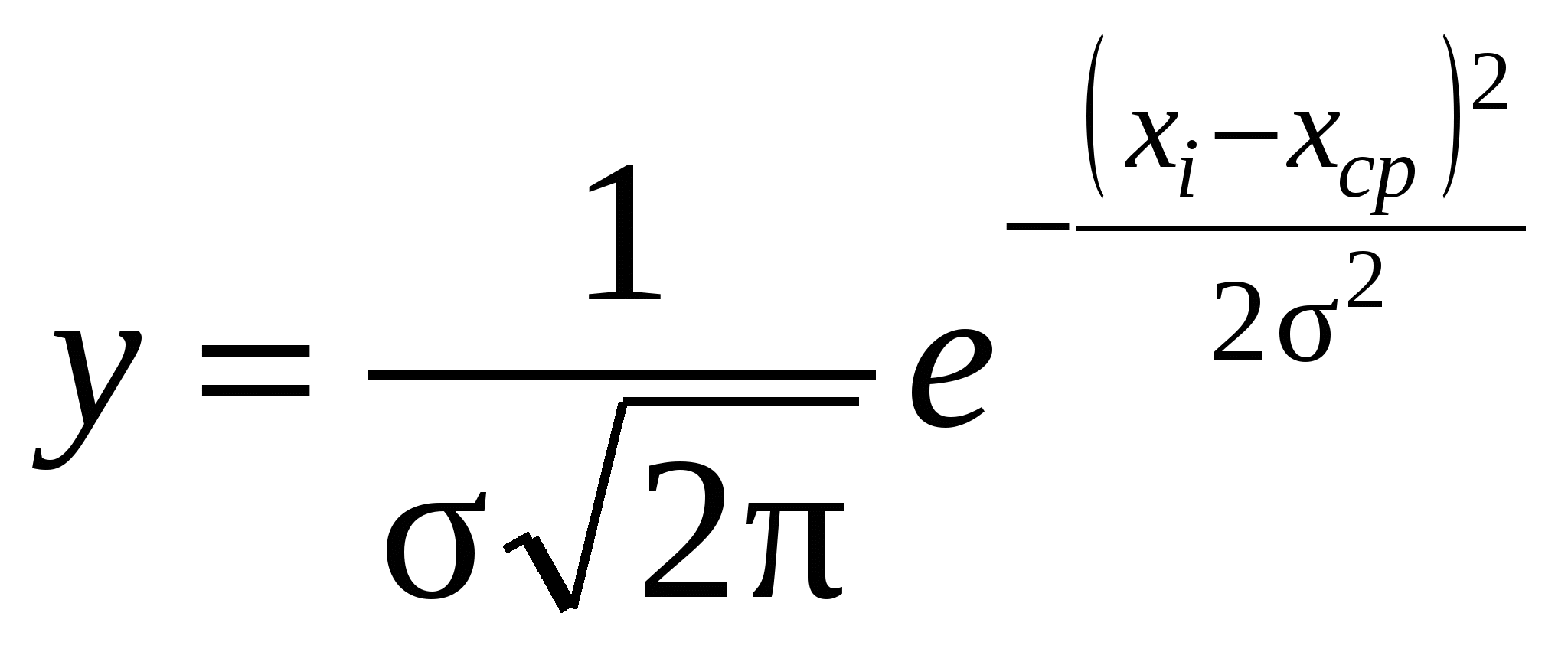 , (4) , (4)где у – функция нормального распределения; σ – среднее квадратичное отклонение; хi – конкретный размер детали; хср – среднее арифметическое размеров деталей данной партии, где n – количество деталей в партии. Кривая нормального распределения изменяется от - ∞ до + ∞. Распределение размеров имеет реальные границы, которые определяются полем рассеивания W = 6σ (рис. 75). Вероятность попадания размеров детали в заштрихованные области – 0,27%.  Рис. 75. Характеристики кривой нормального распределения размеров Мерой рассеивания является величина σ, показывающая, насколько тесно сгруппированы размеры деталей около центра группирования. Мерой центра группирования является хср. Свойства нормального распределения 1. Теоретическая кривая нормального распределения симметрична относительно центра группирования (рис. 75). 2. Чем больше рассеивание, тем шире поле рассеивания, меньше ордината у, σ3>σ2>σ1 (рис. 76, а). 3. При неизменном рассеивании, но различной величине центра группирования, кривая смещается, не изменяя своей формы, σ1 = σ2 , хср2 >хср1 (рис. 76, б).
а) б) Рис. 76. Кривые распределения: а – при различных σ и постоянном значении xср; б – при различных xсрi и постоянном значении σ Второе свойство характерно при изменении действия случайных причин. Это свойство используется для оценки случайных погрешностей при условии ∆сис = const. Третье свойство характерно при изменении действия систематических причин. Используется для оценки систематических погрешностей при условии ∆сл = const. На практике кривая распределения часто отклоняется от теоретического распределения, что учитывается соответствующими коэффициентами: коэффициентом относительной ассиметрии α (рис. 77, а), коэффициентом относительного рассеивания k (рис. 77, б).
а) б) Рис. 77. Кривые распределения при различных коэффициентах: а – относительной ассиметрии α; б – относительного рассеивания k Коэффициент относительной ассиметрии можно определить по формуле где  Рис. 78. Параметры кривой рассеивания, отличающейся от теоретического распределения Коэффициент относительного рассеивания можно определить по формуле Использование свойств нормального распределения для анализа точности при механической обработке По кривой распределения можно оценить точность обработки. 1. Определить величину случайной погрешности ∆сл. Для этого делают выборку деталей, их измеряют, определяют хср, σ, 6σ = ω. Величина случайной погрешности ∆сл приравнивается величине поля рассеивания ω (рис. 79, а) ∆сл = ω. (8) 2. Определить величину систематической погрешности ∆сис. Для этого делают две выборки деталей в разные моменты времени (через один час, два часа, посменно – время выбирается в зависимости от условий). Детали измеряют и определяют хср1 и хср2, находят ∆сис (рис. 79, б) ∆сис = хср2 - хср1. (9)
а) б) Рис. 79. Иллюстрация величины: а – случайной погрешности ∆сл; б – систематической погрешности ∆сис, при условии σ1= σ2 3. Сравнить точность обработки на различных станках. Прежде чем приступить к оценке точности, проведем анализ. Исходя из соотношения, ∆ = ∆сис + ∆сл , (10) где ∆ - общая погрешность обработки, считаем, что ∆сис подчиняется определенным закономерностям их изменения, поэтому их можно учесть, уменьшить или совсем исключить. Величину ∆сл устранить невозможно. Поэтому можно считать, что ∆, как минимум, оценивается ∆сл, т. е. ∆ = ∆сл . (11) При обработке деталей, чтобы получить размеры в пределах допуска, стараются выдержать соотношение ∆ ≤ Т, (12) где Т – допуск выполняемого размера. Данное соотношение называется условием 100% точности обработки. Исходя из этого условия, можно записать, что ∆сл ≤ Т. (13) Вернемся к нашему вопросу по п.3. Для сравнения точности обработки на различных станках производят две выборки, по одной на каждом станке. Детали измеряют и определяют хср1, хср2, σ1 , σ2, 6σ1 = ω1, 6σ1 = ω2, ω1 = ∆сл1, ω2 = ∆сл 2. По найденным величинам случайных погрешностей находим величины допусков обрабатываемых поверхностей на различных станках Т1 =∆сл1 ; Т2 =∆сл2. По величинам допусков в соответствии с размерами обработанных поверхностей оцениваются их квалитеты Т1 →IТ1 и Т2 →IТ2. Найденная точность обработанной поверхности соответствует точности станка, на котором она выполнена. Оценкой квалитетов IT1 и IT2 сравнивается точность различных станков (рис. 80).  Рис. 80. Иллюстрация величин случайных погрешностей на различных станках 4. Определить погрешность наладки. Производится выборка деталей, их измеряют и определяют хср, считается известным Lн. ∆н = хср – Lн, (14) где ∆н – погрешность наладки, Lн – размер настройки инструмента. 5. Определить возможный процент брака. Расчеты по определению брака будут более точными, если кривая рассеивания будет ближе соответствовать нормальному распределению. В тех случаях, когда имеет место ∆сл > Т, то возможно появление брака (рис. 81). Площадь, ограниченную кривой нормального распределения, можно определить по формуле 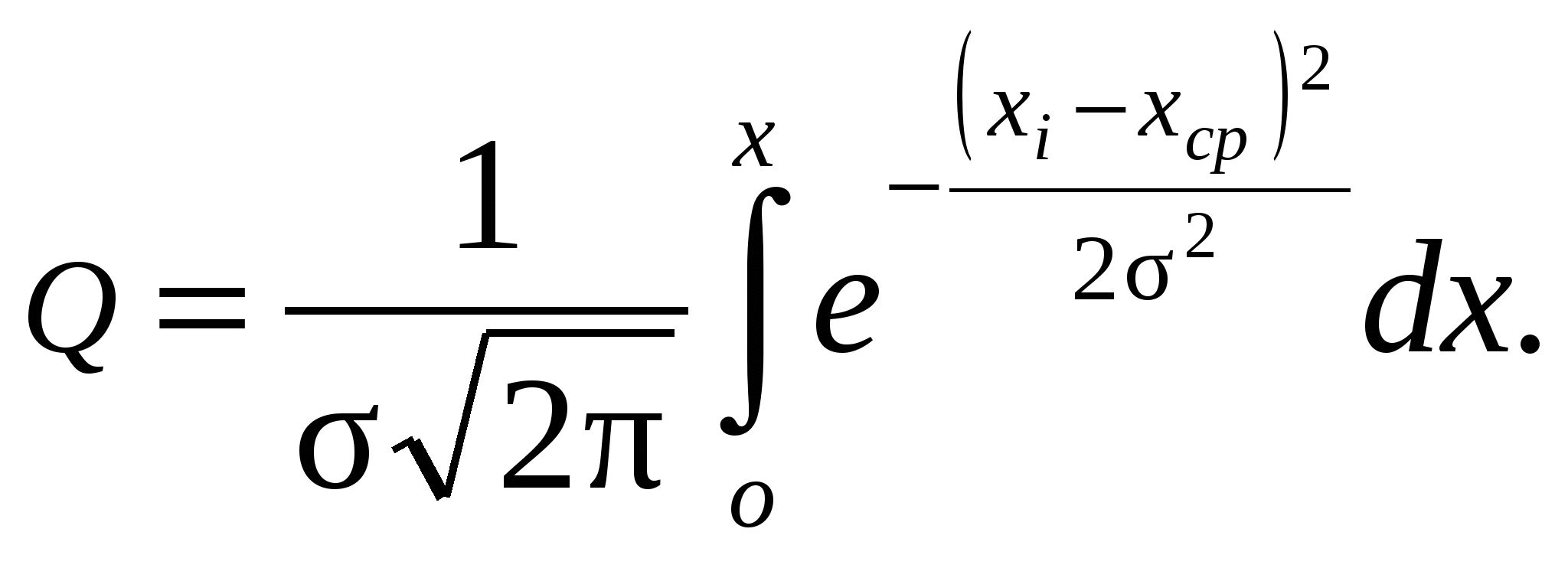 (15) (15) Рис. 81. Иллюстрация к определению возможного процента брака: х – текущее значение размера, σ – средне квадратичное отклонение размеров На рис. 81 брак соответствует заштрихованной площади. Для вычисления величины брака определяется площадь, ограниченная кривой нормального распределения. Количество годных деталей (в %) определяется по формуле (15). Значение Q принимается равным 0,5. Формулу (15) можно записать в виде нормированной функции где Пример: производится обточка валиков, в результате обработки получили среднеквадратичное отклонение σ = 0,09мм. По условию допуск при обработке – Т = 0,36мм. Определить возможный процент исправимого и неисправимого брака, полагая, что кривая распределения близка к нормальному, а центр рассеивания совпадает с серединой поля допуска (рис. 82).  Рис. 82. Пример построения кривой распределения 1. Определяем величину неисправимого брака –х = 0,18, Q1= F(-0,18/0,09) = F(-2) = 0,4772, Fбр1 = 0,5-0,4772 = 0,023→2,3% – неисправимый брак. 2. Определяем величину исправимого брака х = 0,18, Q2= F(2) = 0,4772, Fбр 2 = 2,3% – исправимый брак. Суммарная величина брака Fбр = 4,6%. Следовательно, с помощью анализа кривых рассеивания можно:
Метод точечных диаграмм Метод точечных диаграмм позволяет выявить рассеивание размеров в процессе обработки (во времени). Для построения диаграмм поступают следующим образом: по оси абсцисс откладывают номера последовательно обрабатываемых деталей, а по оси ординат − их размеры (рис. 83).  Рис. 83. Точечная диаграмма при условии ∆сис =const  Рис. 84. Точечная диаграмма при условии ∆сис ≠const При большом количестве обрабатываемых деталей эта диаграмма очень не удобна. Для большего удобства рассмотрим диаграммы, в которых по оси абсцисс откладываются номера групп деталей, а по оси ординат – средние размеры деталей этих групп.  Рис. 85. Точечная диаграмма при большом количестве обрабатываемых деталей Если рассеивание средних размеров подчиняется нормальному распределению, то фактическое поле рассеивания средних размеров будет определяться по формуле где m – количество деталей в группе. Для регулирования технологического процесса вычисляют контрольные границы, выход средних размеров за пределы которых требует вмешательства в процесс с целью регулировки. Для данной диаграммы (рис. 85) контрольные границы будут определяться по формулам где ВКГ и НКГ – верхняя и нижняя контрольные границы средних размеров. Контрольные вопросы
|
