Курс_5. Контрольная по теории информации_2. Основы теории информации
 Скачать 49.92 Kb. Скачать 49.92 Kb.
|
|
Контрольная работа № 2 На тему: Основы теории информации. 1. Дискретная информация характеризуется: - повторными процессами распределения случайной величины - непрерывным процессом изменения некоторой величины + последовательными точными значениями некоторой величины 2. Аналоговая информация характеризуется: - последовательными точными значениями некоторой величины + непрерывным процессом изменения некоторой величины - повторными процессами распределения случайной величины 3. При формальном представлении информации: - ряду однородных объектов ставится в соответствие некий код, позволяющий индентифицировать любой объект из данных однородных объектов по этому коду - совокупности объектов ставится в соответствие формальный код + каждому описываемому объекту или понятию ставится в соответствие некоторый числовой код 4. Специальные таблицы для перевода неформальных данных в цифровой вид называются: - символьные преобразователями + таблицами кодировки - таблицами взаимодействия - таблицами шифрования 5. В таблице кодировки ASCII+ печатные и управляющие символы занимают: + первые 128 позиций таблицы - первые 127 позиций таблицы - все 256 символов таблицы - последние 128 позиций таблицы - последние 127 позиций таблицы 6. Информация может быть нескольких типов: + непрерывная - устойчивая + дискретная - частотная - повторная 7. Информация может быть нескольких типов: + непрерывная - частотная - повторная - устойчивая + дискретная 8. Информация может быть нескольких типов: + непрерывная - частотная + дискретная - повторная - устойчивая 9. Частота дискретизации определяет: - время, в течении которого затухают колебания исследуемой величины - период между измерениями непрерывной величины, колеблющихся разных разных фазах + период между измерениями значений непрерывной величины 10. Общая схема передачи информации имеет вид: + исходная информация - шифровка - сжатие - шумозащитное кодирование - канал связи(проявляется действие шумов) - декодирование шумозащитных кодов - распаковка - дешифровка - полученная информация - исходная информация - шифровка - сжатие - канал связи - распаковка - дешифровка - полученная информация - исходная информация - сжатие - шифрование - шумозащитное кодирование - канал связи(проявляется действие шумов) - декодирование шумозащитных кодов - распаковка - дешифровка - полученная информация - исходная информация - шифровка - сжатие - шумозащитное кодирование - канал связи - декодирование шумозащитных кодов - дешифровка - распаковка - полученная информация - исходная информация - сжатие - шумозащитное кодирование - канал связи - декодирование шумозащитных кодов - дешифровка - полученная информация 11. Клод Шеннон предложил способ изменения количества информации: - средствами визуального определения - путем непосредственного использования символов + содержащейся в одной случайной величине, относительно другой случайной величины 12. Функция f-инъекция, если: - на разных значениях аргумента она принимает одинаковые значения + на разных значениях аргумента она принимает разные значения - она зависит от двух и более аргументов - в роли аргумента выступает функция 13. Если дискретные случайные величины X и Y заданы законами распределения P(X=Xi)=pi, P(Y=Yj)=qj и совместным распределением P(X=Xi,Y=Yj)=pij, то количество информации, содержащейся в X относительно Y равно: 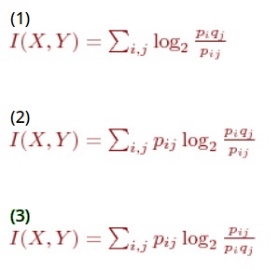 - 1 - 2 + 3 14. Если непрерывные случайные величины X, Y заданы плотностями распределения вероятностей pX(t1), pY(t2) и pXY(t1,t2), то количество информации, содержащейся в X относительно Y равно: 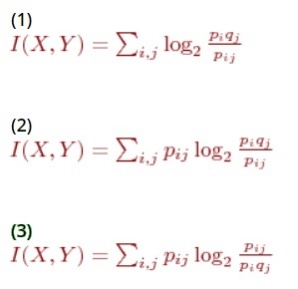 - 1 + 2 - 3 15. I(X,X) = + 1 - 2 - 3 16. Укажите свойства меры информации и энтропии: + 1, 3 - 2, 5 + 4, 6 + 1, 4 - 2, 6 17. Если задана функция inf(s)=-log[sub]2[/]p(s), где s-это предложение, смысловое содержание которого измеряется, p(s) - вероятность истинности s, то эта функция обладает свойствами: + если s-истинно, то inf(s)=0 - inf(s)>=0 + если s[sub]1[/]=>s[sub]2[/] - истинно, то inf(s[sub][/]1)>=inf(s[sub]2[/]) - inf(s)<=0 + если s[sub]1[/]=>s[sub]2[/] - истинно, то inf(s[sub][/]1)<=inf(s[sub]2[/]) 18. Если задана функция inf(s)=-log[sub]2[/]p(s), где s-это предложение, смысловое содержание которого измеряется, p(s) - вероятность истинности s, то если s[sub]1[/]=>s[sub]2[/]: - inf(s[sub]1[/])<=inf(s[sub]2[/]) + inf(s[sub]1[/])>=inf(s[sub]2[/]) - inf(s[sub]1[/])=inf(s[sub]2[/]) 19. Если задана функция inf(s)=-log[sub]2[/]p(s), где s-это предложение, смысловое содержание которого измеряется, p(s) - вероятность истинности s, то: + inf(s)>=0 - inf(s)<=0 + inf(s)=0, при условии, что s - истинно 20. Найти среднюю длину code1 для дискретной случайной величины X: - ML1(X)=2.2 бит/сим - ML1(X)=3.5 бит/сим + ML1(X)=3 бит/сим 21. Найти среднюю длину code2 для дискретной случайной величины X: - ML2(X)=3 бит/сим + ML2(X)=2.2 бит/сим - ML2(X)=3.2 бит/сим 22. Найти среднюю длину code3 для дискретной случайной величины X: + ML3(X)=2.2 бит/сим - ML3(X)=2.8 бит/сим - ML3(X)=3 бит/сим 23. Суть основной теоремы о кодировании при отсутствии помех заключается в том, что: - при очень малой длине n сообщения, при кодировании методом Шеннона-Фэно всего сообщения целиком среднее количество бит на единицу сообщения будет сколь угодно мало отличаться от энтропии единицы сообщения. Данное правило действует только на короткие сообщения - с ростом длины n сообщения, при кодировании методом Шеннона-Фэно всего сообщения целиком среднее количество бит на единицу сообщения будет очень удалено от энтропии единицы сообщения + с ростом длины n сообщения, при кодировании методом Шеннона-Фэно всего сообщения целиком среднее количество бит на единицу сообщения будет сколь угодно мало отличаться от энтропии единицы сообщения 24. Кодирование, основанное на основной теореме о кодировании при отсутствии помех: - легко реализуемо + практически не реализуемо - невозможно 25. Недостатками кодирования, основанного на основной теореме о кодировании при отсутствии помех, являются: + такое кодирование делает невозможным отправку сообщения по частям - отправка сообщения по частям происходит очень медленно - исходная длина кода не должна передаваться вместе с сообщением + необходимость отправки или хранения собственно полученного кода вместе с его исходной длиной 26. Метод Шеннона-Фэно состоит в том, что: - значения дискретной случайной величины располагают в порядке возрастания их вероятностей, а затем последовательно умножают на две части с приблизительно равными вероятностями, к коду первой части добавляют 0, а к коду второй - 1 - значения дискретной случайной величины располагают в порядке убывания их вероятностей, а затем последовательно делят на две части с приблизительно равными вероятностями, к коду первой части добавляют 1, а к коду второй - 0 + значения дискретной случайной величины располагают в порядке убывания их вероятностей, а затем последовательно делят на две части с приблизительно равными вероятностями, к коду первой части добавляют 0, а к коду второй - 1 27. По методу Хаффмена код строится: - на основе реляционной теории + при помощи двоичного дерева - посредством линейной структуры 28. Максимально плотно сжимает метод: + Хаффмена - Шеннона-Фэно - Винера 29. Вычислить длины в битах сообщения "AABCDAACCCCDBB" в коде ASCII+ и его полученного кода + L(AABCDAACCCCDBB) = 62 бит, длина исходного сообщения = 112 бит - L(AABCDAACCCCDBB) = 52 бит, длина исходного сообщения = 94 бит - L(AABCDAACCCCDBB) = 76 бит, длина исходного сообщения = 137 бит 30. Считая, что код генерируется дискретной случайной величиной X с распределением P(X=A)=2/3, P(X=B)=1/3 вычислить длины кодов Хаффмена, блочного Хаффмена (для блоков длины 2 и 3) для сообщения ABAAAB: - LХаффмена-1(ABAAAB) = 5 бит, LХаффмена-2(ABAAAB) = 5 бит, LХаффмена-3(ABAAAB) = 6 бит - LХаффмена-1(ABAAAB) = 5 бит, LХаффмена-2(ABAAAB) = 6 бит, LХаффмена-3(ABAAAB) = 4 бита + LХаффмена-1(ABAAAB) = 6 бит, LХаффмена-2(ABAAAB) = 5 бит, LХаффмена-3(ABAAAB) = 5 бит 31. Считая, что код генерируется дискретной случайной величиной X с распределением P(X=A)=2/3, P(X=B)=1/3 вычислить длину арифметического кода для сообщения ABAAAB: - Lарифметический(ABAAAB) = 2 бита + Lарифметический(ABAAAB) = 1 бит - Lарифметический(ABAAAB) = 1.5 бит 32. Закодировать сообщение "СИНЯЯ СИНЕВА СИНИ", используя адаптивный алгоритм Хаффмена с упорядоченным деревом: + код(СИНЯЯ СИНЕВА СИНИ) = 'С'0'И' 00'Н'100'Я'001100' '101001011100'Е'11000'В'10100'А'1010101101101111 - код(СИНЯЯ СИНЕВА СИНИ) = 'С'0'И' 00'Я'101'Я'001101' '101001011100'С'11110'И'10100'И'1010111101101011 - код(СИНЯЯ СИНЕВА СИНИ) = 'С'0'И' 01'Я'100'Я'111100' '101001011100'Е'11010'В'11100'А'1010111100101010 33. Закодировать сообщение BBCBBC, используя адаптивный алгоритм Хаффмена с упорядоченным деревом: - 'C'01'B'0100 - 'B'11'C'1001 + 'B'10'C'1101 34. Закодировать сообщение "AABCDAACCCCDBB", используя адаптивный алгоритм Хаффмена с упорядоченным деревом: - код(AABCDAACCCCDBB) = 'A'10'B'00'C'011'D'00011001111100110011110 + код(AABCDAACCCCDBB) = 'A'10'B'00'C'000'D'00011001111100110011001 - код(AABCDAACCCCDBB) = 'A'11'B'11'C'010'D'00011001111100110000101 35. Закодировать сообщение "КИБЕРНЕТИКИ", используя адаптивный алгоритм Хаффмена с упорядоченным деревом: + код(КИБЕРНЕТИКИ) = 'К'0'И'00'Б'100'Е'000'Р'1 100'Н'1111000'Т'100110111 - код(КИБЕРНЕТИКИ) = 'К'0'И'00'Б'101'Е'010'Р'1 100'Н'1100001'Т'100110001 - код(КИБЕРНЕТИКИ) = 'К'0'И'00'Б'100'Е'000'Р'1 100'Н'1111000'Т'101010001 36. Вычислить длины в битах сообщения "КИБЕРНЕТИКИ" в коде ASCII+ и его полученного кода - L(КИБЕРНЕТИКИ) = 98 бит, длина исходного сообщения = 102 бита - L(КИБЕРНЕТИКИ) = 72 бита, длина исходного сообщения = 75 бит + L(КИБЕРНЕТИКИ) = 85 бит, длина исходного сообщения = 88 бит 37. Вычислить длины в битах сообщения "СИНЯЯ СИНЕВА СИНИ" в коде ASCII+ и его полученного кода - L(СИНЯЯ СИНЕВА СИНИ) = 104 бит, длина исходного сообщения = 124 бит + L(СИНЯЯ СИНЕВА СИНИ) = 114 бит, длина исходного сообщения = 136 бит - L(СИНЯЯ СИНЕВА СИНИ) = 124 бит, длина исходного сообщения = 148 бит 38. Составить адаптивный арифметический код с маркером конца для сообщения BAABC: + 01000010111001 - 01000011000011 - 01000010110100 39. Распаковать сообщение 'A'0'F'00'X'0111110101011011110100101, полученное по адаптивному алгоритму Хаффмена с упорядоченным деревом - FFXAAAXFXAXFFAA - AFXFFAXFXAXAAAF + AFXAFFXFXAXAFFA 40. LZ77 и LZSS обладают следующими очевидными недостатками: + невозможность кодирования подстрок, отстоящих друг от друга на расстоянии, большем длины словаря - длина подстроки, которую можно закодировать, ограничена размером оперативной памяти компьютера + длина подстроки, которую можно закодировать, ограничена размером буфера 41. При чрезмерном увеличении размера словаря и буфера для алгоритмов LZ77 и LZSS, то это приведет: - к снижению стойкости кода - к увеличению эффективности кодирования + к снижению эффективности кодирования 42. "Скользящее" окно НЕ использует алгоритм: - LZ77 + LZ78 - LZSS 43. Закодировать сообщения "СИНЯЯ СИНЕВА СИНИ", вычислить длины в битах полученных кодов, используя алгоритм LZW (словарь - ASCII+ и 16 фраз): + 0'C'0'И'0'Н'0'Я'0'Я'0"(256)0'Н'0'Е'0'В'0'А'(257)О'И', длина 14 * 9 = 126 бит - 0'C'0'И'0'Н'0'Я'0"(261)0'Н'0'Е'0'В'0'А'(256)(256)О'И', длина 13 * 9 = 117 бит - 1'C'1'И'0'Н'0'Я'1'Я'0"(256)0'Н'1'Е'0'В'0'А'(256)(261)О'И', длина 12 * 9 = 108 бит 44. Запатентованным является алгоритм: - LZ78 - LZSS + LZW 45. Закодировать сообщения "AABCDAACCCCDBB", вычислить длины в битах полученных кодов, используя алгоритм LZ77 (словарь - 12 байт, буфер - 4 байта): - (0,0,'А')(10,1,'В')(1,0,'C')(11,1,'D')(7,2,'D')(11,2,'C')(5,2, 'B')(0,0,'B'), длина 8 * 13 = 104 бита + (0,0,'А')(10,1,'В')(1,0,'C')(11,1,'D')(7,2,'D')(11,2,'C')(5,2, 'B')(0,0,'B'), длина 8 * 15 = 120 бита - (0,0,'А')(11,1,'С')(0,0,'C')(10,10,'С')(8,2,'С')(7,11,'C')(7,8, 'B')(10,0,'B'), длина 8 * 10 = 80 бита |
