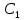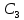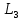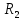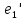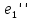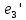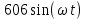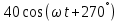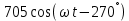Задачи. Основная часть Расчет электрической цепи постоянного тока
 Скачать 7.24 Mb. Скачать 7.24 Mb.
|
Основная частьРасчет электрической цепи постоянного токаЗадача № 1 Упростить схему, заменив последовательно и параллельно соединенные резисторы четвертой и шестой ветвей эквивалентными. Дальнейший расчет вести для упрощенной схемы. Определить токи во всех ветвях схемы методом контурных токов. Составить на основании законов Кирхгофа систему уравнений для расчета токов во всех ветвях схемы. Определить токи во всех ветвях схемы методом узловых потенциалов. Результаты расчета токов, проведенного двумя методами, свести в таблицу и сравнить между собой. Составить баланс мощностей в исходной схеме (схеме с источником тока) вычислив суммарную мощность нагрузок (сопротивлений). Определить ток I1 в заданной по условию схеме с источником тока, используя метод эквивалентного генератора. Начертить потенциальную диаграмму для любого замкнутого контура включающего обе ЭДС. Таблица 1.1- Исходные данные варианта 79.
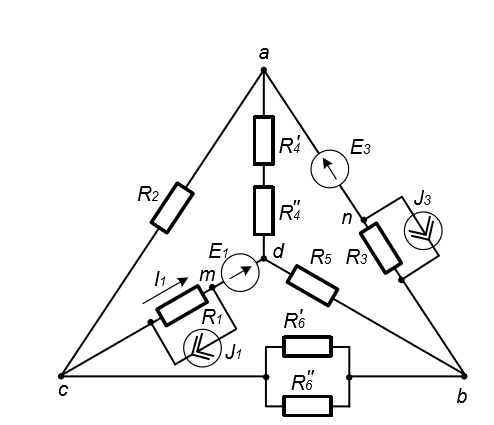 Рис. 1. 1 Исходная электрическая схема цепи 1. Упростим схему, заменив последовательно и параллельно соединенные резисторы четвертой и шестой ветвей эквивалентными. Дальнейший расчет вести для упрощенной схемы. 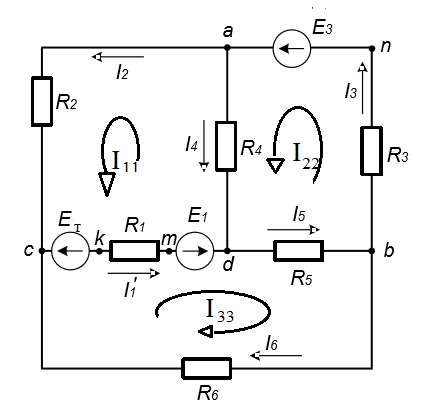   R4 = R'4 + R"4= 5+5= 10 (Ом); R6 = (R'6 * R''6) / (R'6 + R''6) = (175*70) / (175+70) = 50 (Ом); EТ = R1J1 = 0,6*12,5 = 7,5 (В). 2. Определим токи во всех ветвях схемы методом контурных токов. Выбираем независимые контуры и направления контурных токов в каждом из них(I11, I22, I33). На основании второго закона Кирхгофа составляем систему уравнений для контурных токов I11, I22, I33:  к11: (R1+R2+R4)I11– R4I22 +R1I33 =Е1-Eт к11: (R1+R2+R4)I11– R4I22 +R1I33 =Е1-Eтк22: –R4I11 + (R3+R4+R5)I22+R5I33 = Е3 к33: R1I11+R5I22 + (R1+R5+R6)I33 = E1 – ET Подставляем значения R и Е в данной системы:  к11: (12,5+17,5+10)I11 –10I22 + 12,5I33 =45-7,5 к11: (12,5+17,5+10)I11 –10I22 + 12,5I33 =45-7,5к22: –10I11 + (25+10+37,5)I22 +37,5I33 =75 к33: 12,5 I11 + 37,5I22 + (12,5+37,5+50)I33 =45– 7,5  к11: 40I11 – 10I22 +12,5I33 = 37,5 к11: 40I11 – 10I22 +12,5I33 = 37,5к22: –10I11 + 72,5I22 +37,5I33 = 75 к33: 12,5I11 +37,5I22 + 100I33 = 37,5 Находим контурные токи, используя определители: Δ = 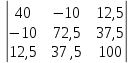 = 203046.875 = 203046.875Δ1 = 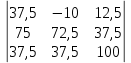 = 281250 = 281250Δ2 = 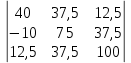 = 282421.875 = 282421.875Δ3 = 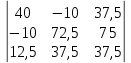 = −64921.875 = −64921.875I11 = 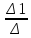 = = 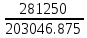 = 1,385 (А) = 1,385 (А)I22 = 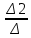 = = 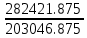 = 1,391 (А) = 1,391 (А)I33 = 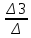 = = 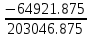 = -0,319 (А) = -0,319 (А)Выразим истинные токи через контурные: I'1= I11+I33=1,385-0,319=1.065 (А) I2=I11 = 1,385 (A) I3=I22=1,391 (A) I4=I22–I11=1.391–1,385 =0,006 (A) I5=I22+I33=1,391–0,319=1,071 (A) I6=I33= -0,319 (A) В ветви, содержащей ET, истинное значение тока I1 находим по исходной схеме, используя первый закон Кирхгофа для узла m, предварительно проставив направление найденного значения I’3 и заданного J1: I1= I’1 + J1 = 1,065+ 1= 2,065 (A) 3. Составим на основании законов Кирхгофа систему уравнений для расчета токов во всех ветвях схемы. Осуществляем проверку найденных токов по 1-му закону Кирхгофа:  узел a: I2 + I4 –I3= 0 узел a: I2 + I4 –I3= 0 узел b: I3– I5 + I6 = 0 узел c: I1 - I6 – I2–J1 = 0 узел d: I5 – I1 – I4 +J1=0  узел a: 1,385 + 0,006– 1,391= 0 узел a: 1,385 + 0,006– 1,391= 0узел b: 1,391– 0,319 – 1,071= 0 узел c: 2,065+0,32 – 1,385– 1= 0 узел d: 1,07 – 2,065 – 0,006+ 1 =0 Осуществляем проверку найденых токов по 2-му закону Кирхгофа:  к11: R1I1+R2I2 – R4I4= E1 к11: R1I1+R2I2 – R4I4= E1к22: R3I3 +R4I4+R5I5 = Е3 к33: R1I1 + R5I5+ R6I6 = E1  к11: 12,5*2,065 +17,5*1,386 – 10*0,006=29,994 к11: 12,5*2,065 +17,5*1,386 – 10*0,006=29,994к22: 25*1,391 +10*0,006 +1.075*37,5 = 44,9985 к33: 12,5*2,065 + 37,5*1,072 – 70*0,319 = 30.015  к11: 29,994 ≈ 30 (В) к11: 29,994 ≈ 30 (В)к22: 44,9985 ≈ 45 (В) к33: 30,015 ≈ 30 (B) 4. Определим токи во всех ветвях схемы методом узловых потенциалов. Система для расчета потенциалов в узлах, составленная из схемы: Рис 1.2.  узел a: (g2+g3+g4)φa – g3φb– g2φc = E3g3 узел a: (g2+g3+g4)φa – g3φb– g2φc = E3g3узел b: –g3φa + (g3+g5+g6)φb– g6φc = – E3g3 узел c: –g2φa–g6φb+ (g1+g2+g6)φc =(ET – E1)g1 Найдем проводимости ветвей: g1=1/R1=1/12,5= 0,08 (Oм-1) g2=1/R2=1/17,5= 0,057 (Oм-1) g3=1/R3=1/25= 0,04 (Oм-1) g4=1/R4=1/10= 0,1 (Oм-1) g5=1/R5=1/37,5= 0,026 (Oм-1) g6=1/R6=1/50= 0,02 (Oм-1) Подставляем коэффициенты g и E данную систему:  узел a: 0,197φa – 0,04φb – 0,057φc = 3 узел a: 0,197φa – 0,04φb – 0,057φc = 3узел b: –0,04φa + 0,086φb– 0,02φc = – 3 узел c: – 0,057φa– 0,02φb+ 0,157φc = – 3 Находим потенциалы узлов, используя определители: Δ = 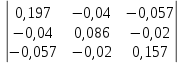 = 0,00914916 = 0,00914916Δ1 = 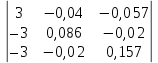 = 0,00187033557 = 0,00187033557Δ2 = 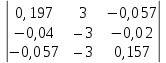 = – 0,22052129 = – 0,22052129Δ3 = 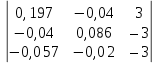 = – 0,13274521 = – 0,13274521φa= 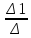 = = 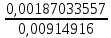 = 0,031 (B) = 0,031 (B)φb = 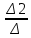 = = 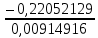 = –24,1029 (B) = –24,1029 (B)φc = 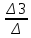 = = 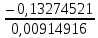 = –14,509 (B) = –14,509 (B)φd = 0 (B) Находим истинные токи: I'1= (φc – φb+E1-Eт)g1 = (-14,509+30-7,5)*0,1333 = 1,065 (A) I2 = (φa– φc )g2 = ( 0,0317-14,509)*0,0952 = 1,384 (А) I3=(φb – φa + E3 )g3=(-24,1029-0,0317+45)*0,0666 = 1,389 (А) I4=(φa – φd)g4= (0,0317-0)*0,1666 = 0,005 (А) I5=(φd – φb)g5=(0 +24,1029)*0,444= 1,074 (А) I6=(φc – φb)g6=(–14,509+24,1029)*0,333 = 0,319 (А) 5. Результаты расчета токов, проведенного двумя методами, свести в таблицу и сравнить между собой. Таблица 1.2 - Результаты расчета токов.
6. Составить баланс мощностей в исходной схеме (схеме с источником тока) вычислив суммарную мощность нагрузок (сопротивлений). Pист. эн. =Pнагрузки Pист. эн. = J1I1R1 + E3I3 + E1I’1 =0,6*12,5*2,065+75*1,391+45*1,06= 15,4875+104,325+47,7= 167,5125 (Вт) Pнагрузки=I12R1 + I22R2 + I32R3 + I42R4 + I52R5 + I62R6 = 34,65+33,714 + 48,37 + 0.00036 + 43,014+5,088 = 167,836 (Вт) 167,5125 = 167,836 (Вт) Допускается расхождение баланса активных мощностей ΔP= 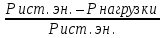 *100%= *100%= 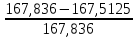 *100%= 0,19% <0,5% *100%= 0,19% <0,5% 7. Определим ток I2 в заданной по условию схеме с источником тока, используя метод эквивалентного генератора. Выделим ветвь с I2 из схемы, а оставшуюся часть схемы представим в виде активного двухполюсника – эквивалентного генератора. 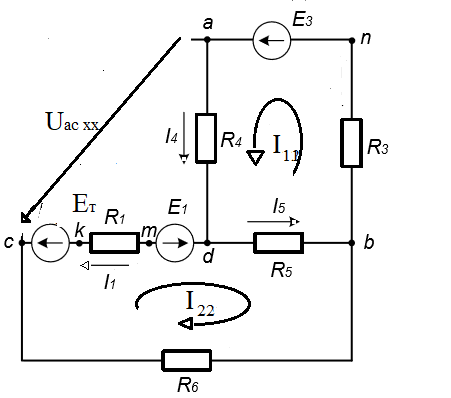 Рис 1. 4 Схема цепи с оборванной ветвью I2 = Uac xx/(Rвх+ R1) Для нахождения Uac xx применим метод контурных токов:  к11: (R3+R4+R5)I11 + R5I22 = Е3 к11: (R3+R4+R5)I11 + R5I22 = Е3к22: R5I11 + (R1+R5+R6)I22 = E1 – ET Подставляем значения R и E в данную систему:  к11: (25 + 10 + 37,5)I11 + 37,5I22 = 75 к11: (25 + 10 + 37,5)I11 + 37,5I22 = 75к22: 37,5I11 + (12,5 + 37,5 + 50)I22 = 37,5  к11: 72,5I11 + 10I22 = 75 к11: 72,5I11 + 10I22 = 75к22: 10I11 + 100I22 = 37,5 Находим контурные токи, используя определители: Δ= 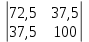 = 5843.75 = 5843.75Δ1= 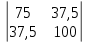 = 6093.75 = 6093.75Δ2= 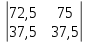 = −93.75 = −93.75I11 = 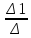 = = 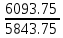 = 1,052 (А) = 1,052 (А)I22 = 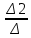 = = 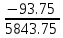 = -0,0337 (А) = -0,0337 (А)Рассчитаем истинные токи в ветвях: I1 = I22 = |-0,0337|=0,0337 (A) I4=I11= 1,052 (A) Выразим Uac xxпо второму закону Кирхгофа: Uac xx – I1R1 – I4R4 = E1–Eт Uac xx= I1R1 + I4R4 +E1–Eт = 45-7,5+10*1,052+12,5*0,0337 = 48,441 (В) Внутреннее сопротивление эквивалентного источника равно входному сопротивлению относительно выводов « c-a » пассивного двухполюсника. Входное сопротивление двухполюсника относительно выводов «c-a» определяется при устранении из схемы активного двухполюсника всех источников (ветви с источниками тока разрываются, а источники ЭДС в ветвях закорачиваются). 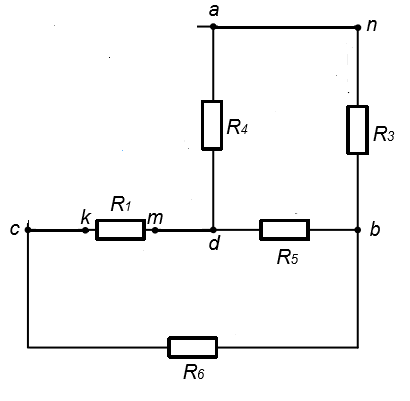 Рис. 1.4 Схема без источников ЭДС Чтобы рассчитать Raх.bc нужно свернуть цепь, то есть предварительно от треугольника R4, R3, R5 перейти к эквивалентной звезде Ra, Rb, Rd: 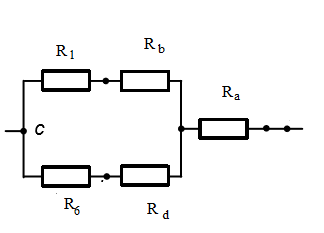 Рис. 1.5 Схема замещения (пассивная) Рассчитаем сопротивления лучей эквивалентной звезды: 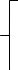 Ra=(R3R4)/(R3+R4+R5)=(25*10)/(25 + 10 + 37,5)= 3,448 (Ом) Rb=(R4R5)/( R3+R4+R5)=(10*37,5)/( 25 + 10 + 37,5) = 5,17 (Ом) Rd=(R3R5)/( R3+R4+R5)=(25*37,5)/(25 + 10 + 37,5 ) = 12,93 (Ом) Rвх.BC = Ra + (Rb + R1)*(Rd + R6) / (Rd + R1 + Rb + R6) = 3,448 + (5,17 + 12,5)*(12,93 + 50) / (5,17+ 12,5 + 12,93 + 50) = 17,2445 (Ом) Подставим найденные значения Rвх.ac и Uac xx и найдем I2: I2 = Uac xx/(Raх.bc+ R2) = 48,441/ (17,2445 + 17,5) = 1,394 (A) 8. Начертить потенциальную диаграмму для любого замкнутого контура включающего обе ЭДС. Потенциальная диаграмма для контура "cmdbnac" φc= 0 (B) φm= φc – R1I1 = – 15,49 (B) φd= φm – E1= – 15,49 + 30 = 14,51 (B) φb= φd –I5R5 = 14,51 – 22,5*1,071 = -9,58 (B) φn= φb – R3I3 = -9,58 – 20,865 = – 30,45 (B) φa= φn + E3= –30,45 + 45 = 14,55 (B) φc= φa – R2I2= 14,55 – 14,54 = 0,01 ≈ 0 (B)  Рис. 1.6 Потенциальнвя диграмма II. Расчет цепи переменного синусоидального токаЗадача 2. Определить комплексы действующих значений токов во всех ветвях, воспользовавшись одним из методов расчета линейных электрических цепей. По результатам, полученным в пункте 1, определить показания ваттметра. Построить совмещенную векторную диаграмму для токов и напряжений. На основании законов Кирхгофа составить в общем виде систему уравнений для расчета токов во всех ветвях цепи в двух формах: дифференциальной и символической. Таблица 2.1. Исходные данные варианта 79
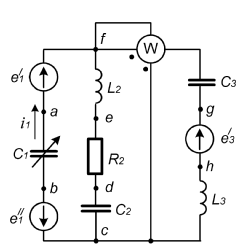 Рис. 2.1 Исходная схема цепи Упростим схему цепи, обозначив комплексы всех величин: 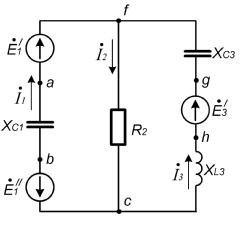 Рис. 2.2 Упрощенная схема цепи. Находим комплексные значения действующих ЭДС: 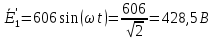 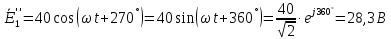 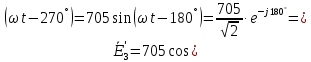 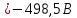 Производим расчет угловой частоты: 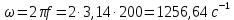 Находим величины сопротивлений всех реактивных элементов цепи: 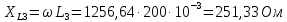 71 го тока. 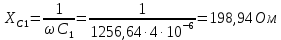 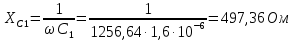 Составим систему уравнений по методу контурных токов: 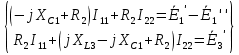 Подставляем известные 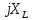 , , 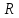 , , 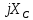 и и 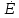 : :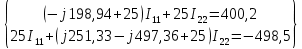 Подсчитываем коэффициенты: 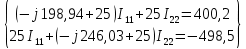 Решаем полученную систему методом Крамера; вычисляем определители системы: 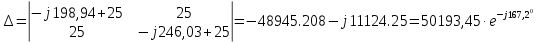 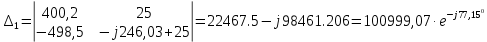 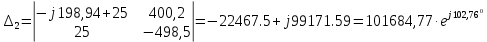 Находим контурные токи: 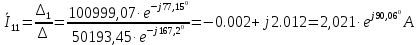 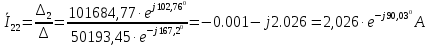 Перейдем от контурных токов к токам в ветвях: 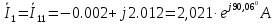 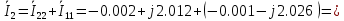 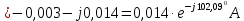 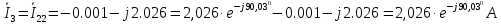 Рассчитываем показания ваттметра: 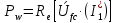 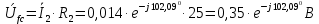 Находим сопряжённый комплекс: 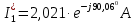 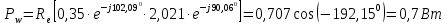 Рассчитываем падения напряжений для построения векторной диаграммы: 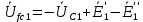 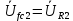 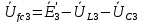 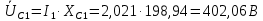 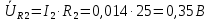 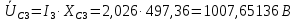 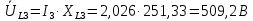 Составим уравнения на основании законов Кирхгофа. Дифференциальная форма:  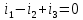 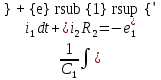 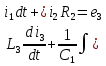  Символическая форма: Символическая форма: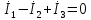 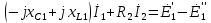 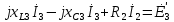 Построим потенциальную диаграмму, выбрав m 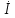 =1 А/см, m =1 А/см, m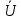 =200 В/см: =200 В/см: 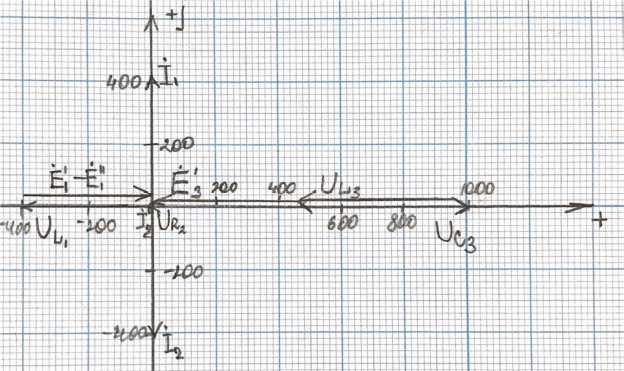        III. Расчет переменной трехфазной цепи синусоидального токаРассчитать токи; Определить мгновенное значение напряжения между точками b c; Подсчитать активную мощность трехфазной системы; Построить векторную диаграмму токов и напряжений. Таблица 3.1 -Исходные данные варианта № 79
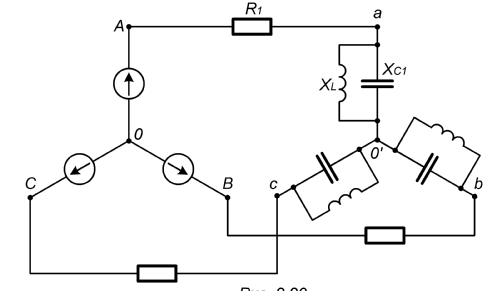 Рис. 3.1 – Исходная схема электрической цепи Для того, чтобы найти токи, необходимо, в первую очередь, рассчитать комплексные действующие значение ЭДС генератора: 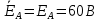 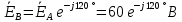 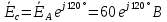 Угловая частота колебаний: 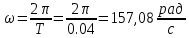 Сопротивления реактивных элементов: 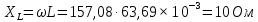 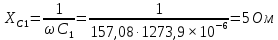 Рассчитаем сопротивление участка ao’: 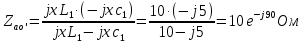 Рассчитаем общее сопротивление одной фазы: 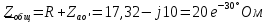 Теперь рассчитаем токи: 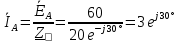 А А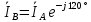 А А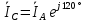 А АОпределим мгновенное значение напряжения между заданными точками b, c. 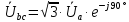 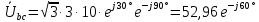 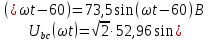 Далее подсчитаем активную мощность трехфазной системы: Далее подсчитаем активную мощность трехфазной системы:P = 3PA Pa = Re[ 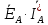 ] ]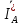 = 3 = 3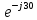 (A) (A)Pa = Re[60*3 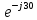 ] = Re[180 ] = Re[180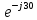 ] = 155 Вт ] = 155 ВтР = 3*155 = 465 Вт Теперь построим совмещенную векторную диаграмму токов и напряжений на каждом участке цепи. Для этого рассчитаем необходимые падения напряжений: 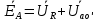 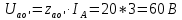 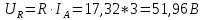 С 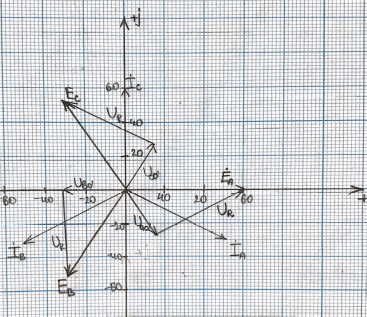 троим диаграмму, учитывая направления токов и напряжений. троим диаграмму, учитывая направления токов и напряжений. mU = 20 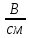 mI = 1 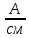 Рис. 3.2 – Совмещенная векторная диаграмма токов и напряжений | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||