Лекции. Основные понятия и определения

• Название: Основные понятия и определения
• Дата: 27.03.2018
• Размер: 1.94 Mb.
• Имя файла: Лекции.docx
• Тип: Контрольные вопросы; #39570
• страница: 50 из 58

ЗАДАЧИ

Элементарные конструкции

1. Какие нижеприведенных записей являются можно использовать в качестве имен:

X Begin a[3] 3D_Studuo Step1 sin(x) CTEK a15x Str.X α1 конец _XX x_x

2. Какие из записей ниже являются целыми литералами:

0 +006 -45 3. .55 0712 &034 0xabc 0X12a5 &habc &H12A5

3. Какие из записей ниже можно считать литералами с плавающей точкой:

-123.4 34.05 75. -.05 0.0123 -34.593E-12 -2e5 1D15 d-23 1e1 -1e-1.2 0E-3

4. Записать на языках C и Basic следующие арифметические выражения:

a)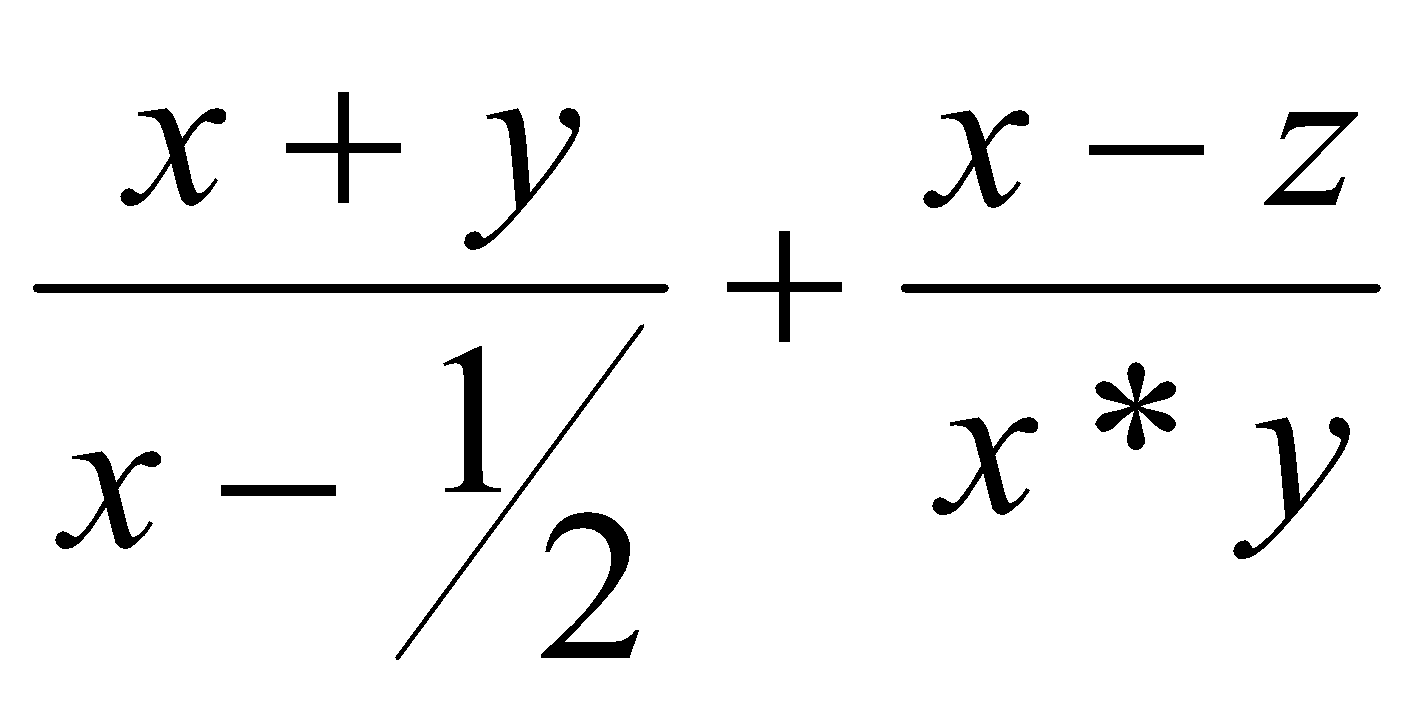

б)

в)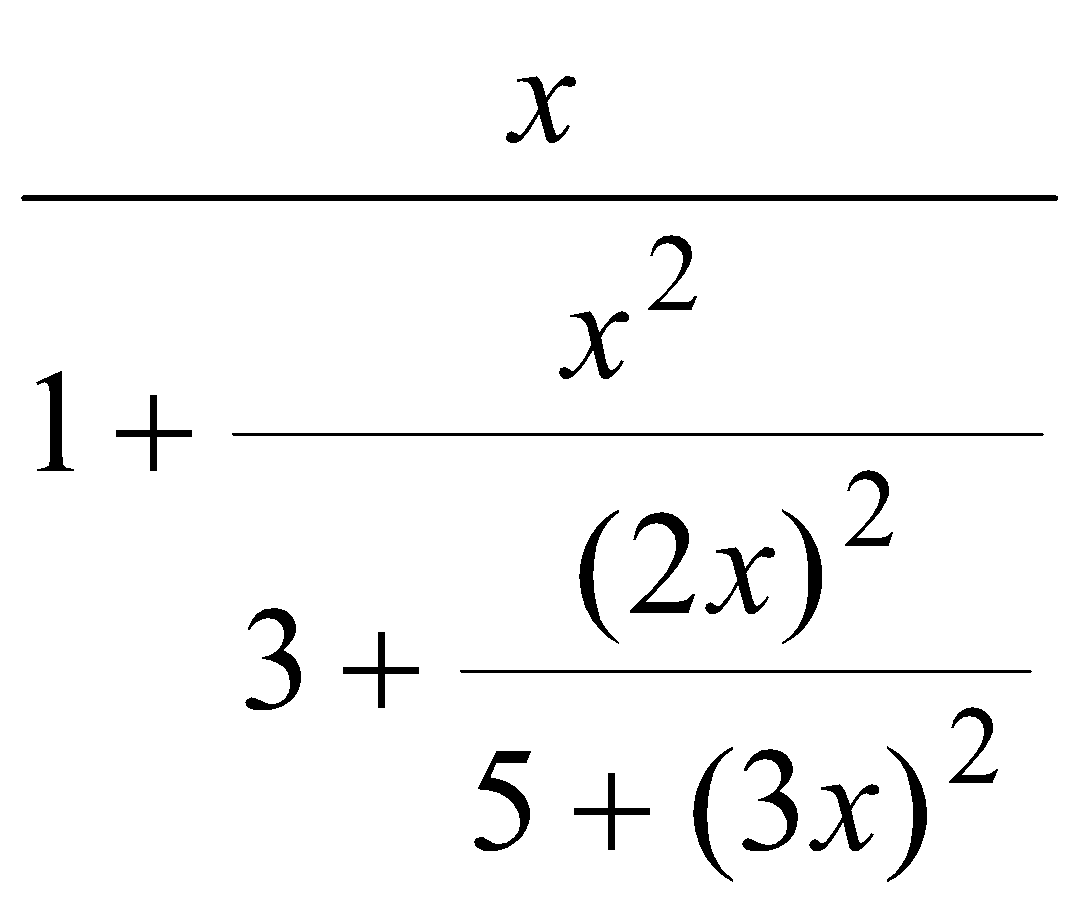

г)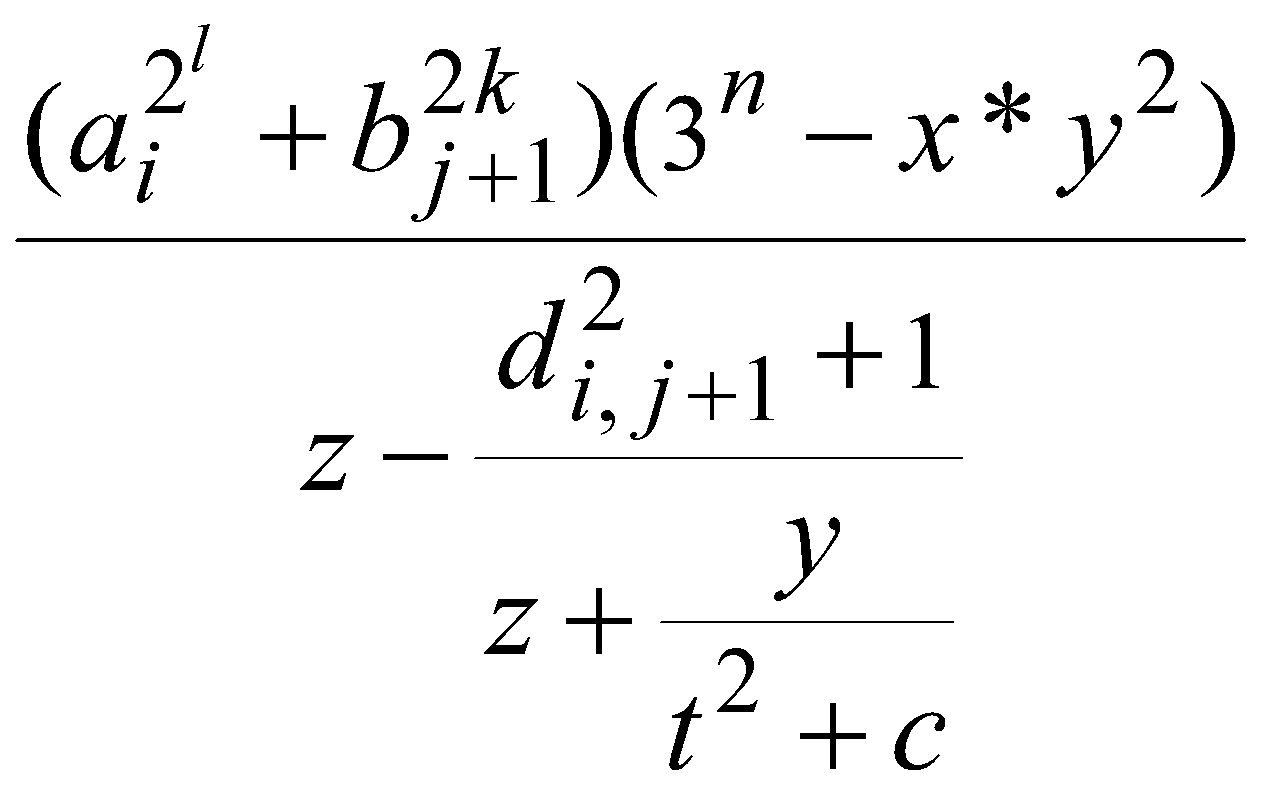

д)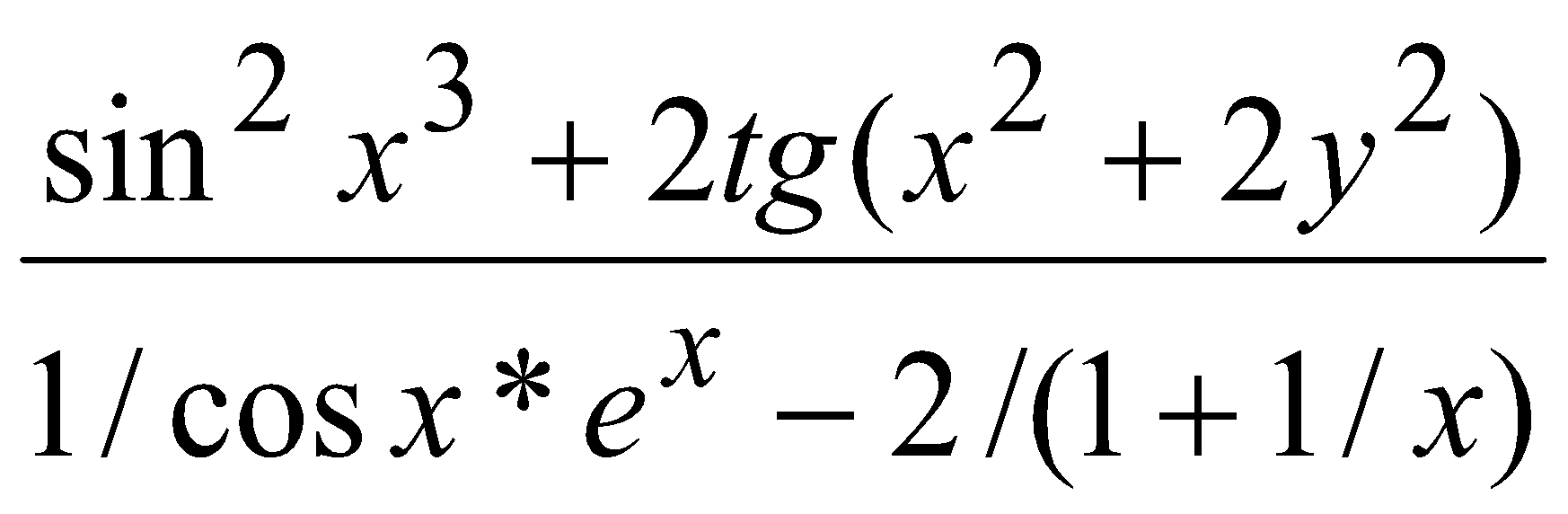

е)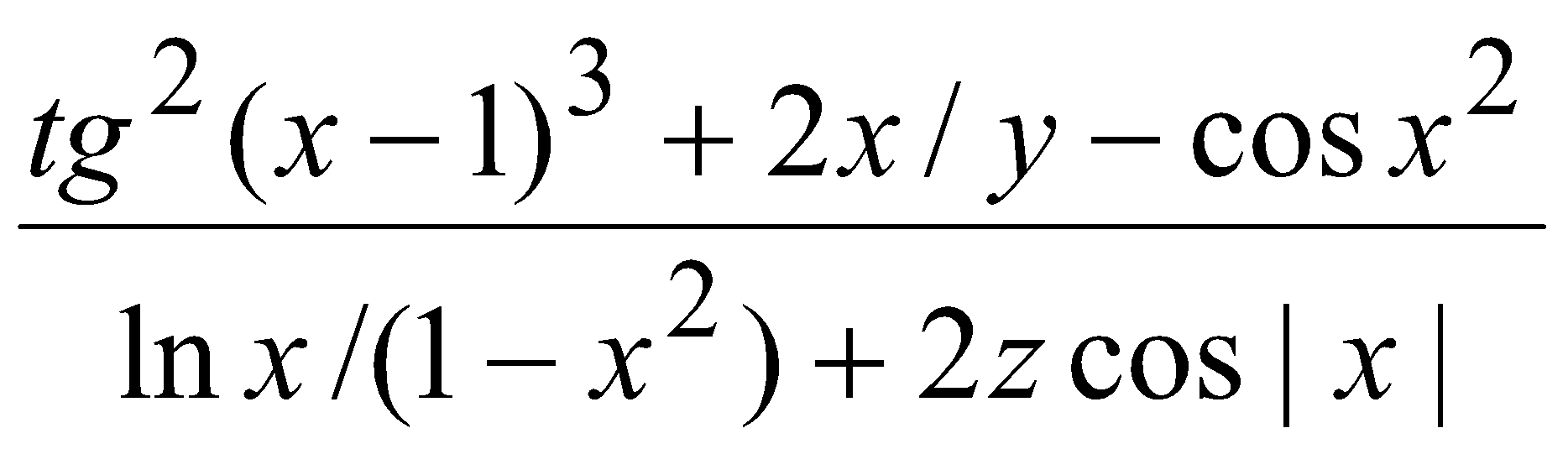

5. Определить число сотен натурального числа.

6. Дано трехзначное натуральное число n. Записать его в обратном порядке, например, 456 → 654.

7. Записать логическое выражение, принимающее значение true, если точка М(x,y) попадает в заштрихованную область:

a) y б) y

1 1

x -1 1 x

1 2

-1

в) y г) y

2

2

-2 1 1 2 x -1 1 x

-2 -2

8. Записать логическое выражение, принимающее значение true, если из отрезков с длинами x, y, z можно составить треугольник.

9. Начертить на плоскости XY области, в которой перечисленные ниже выражения принимают значения true(выражения записаны на языке C):

а) x²+y²<=1 || x>0

б) x>y == y>0

в) x+y<=1 || x>=0 && !(y<0)

г) x²+y²<1 && y>=x ==y>.5

Простые циклы

1. Вычислить и напечатать таблицу функции:

2x³/(x²+1), если |x|<3

y =

1.5|tg π/x|, если |x|>=3.

x изменяется от –6 до 6 с шагом Δx=1.

2. Вычислить и напечатать таблицу функции:

e^-x sin 2x, если x<0.4

y =

ln x cos πx, если x>=0.4.

x изменяется от –2 до 2 с шагом Δx=0.2.

3. Найти сумму ряда u_n=n/(n²+1), n=1...∞. Вычисления прекратить при достижения условия u_n < 10^-5.

4. Найти сумму элементов последовательностей, заданных ниже. Вычисления прекратить при выполнении условия: |u_n|<10^-5.

а) u_n=xⁿ/(2n)! б) u_n=x²ⁿsin(xⁿ)/n².

5. Вычислить cos 15x по формуле:

cos nx = cos (n-1)x cos x – sin (n-1)x sin x,

где cos x = 0.15, sin x = √(1 – cos²x).

6. Дано целое M(M > 1). Найти наибольшее целое к, при котором 4^k < M.

7. Дан массив: {x_i}, i = 1...n. Переставить элементы массива в обратном порядке. Вспомогательный массив не использовать.

8. Дан массив: {x_i}, i = 1...n. Найти максимальный по модулю элемент массива.

9. Дан массив: {x_i}, i = 1...n. Сформировать массив {y_i}, i = 1...n по правилу:

{x_n, ..., x₃, x₁, x₂, x₄, ..., x_n-1}.

10. Дан массив: {x_i}, i = 1...n, задающий рост студентов в группе. Определить, выстроены ли они по росту.

11. Дан массив: {x_i}, i = 1...n. Определить число "соседств" 2-х положительных чисел.

12. Дан массив: {x_i}, i = 1...n. Найти максимальный и минимальный элементы и поменять их местами.

13. Даны массивы: {x_i}, i = 1...n, {y_i}, i = 1...n. Преобразовать их элементы следующим образом: x_i=max(x_i,y_i), y_i= min(x_i,y_i).

14. Дан массив: {x_i}, i = 1...n. Найти сумму элементов, меньших максимального.

15. Дан массив: {x_i}, i = 1...n. Поменять местами наибольший из отрицательных и наименьший из положительных элементов.

16. Дан массив: {x_i}, i = 1...n. Сформировать массив {y_i}, i = 1...n по правилу: расположить все неотрицательные элементы массива x в порядке их следования, затем все отрицательные.

17. Вычислить: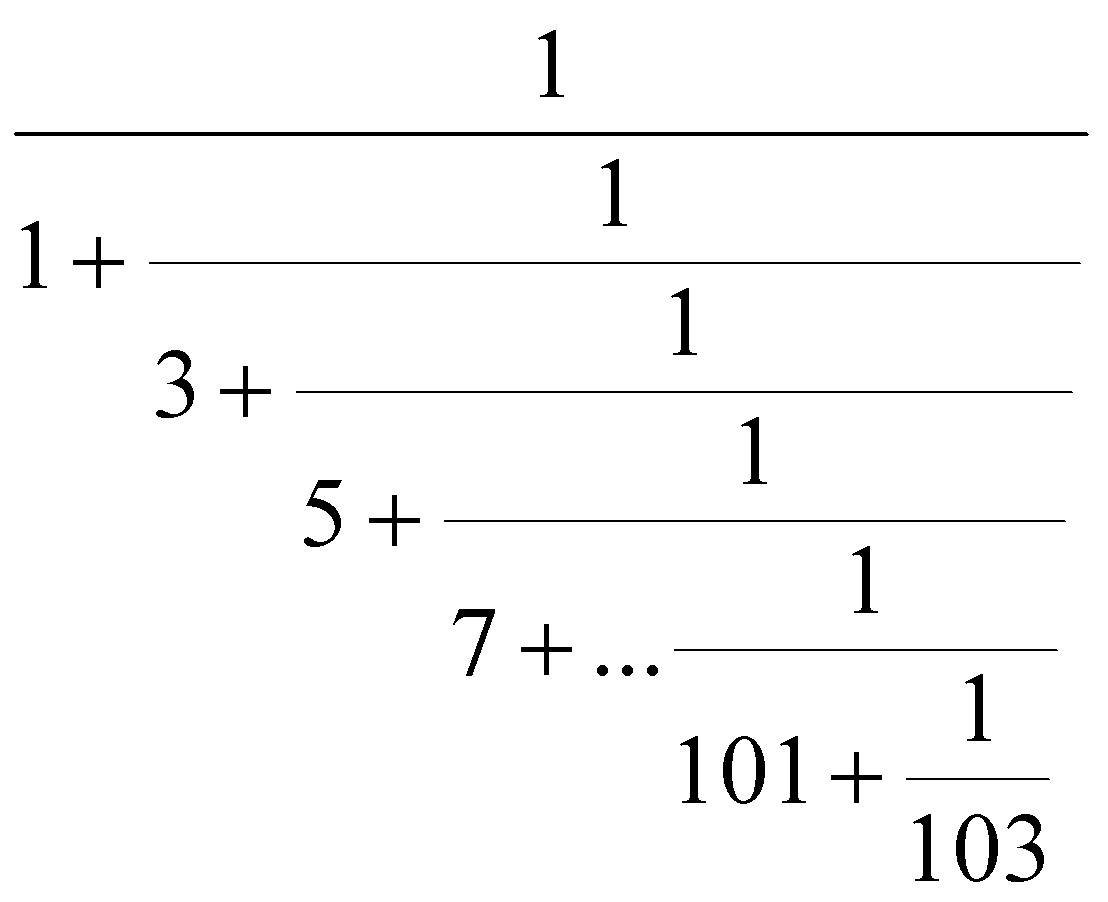



18. Дан целый массив: {x_i}, i = 1...n. Выбросить из него все элементы, равные max x_i.

19. Дан массив: {x_i}, i = 1...n. Найти Σy_kz_k, где y_k – отрицательный элемент массива {x_i} в порядке следования, z_k – неотрицательный элемент того же массива в обратном порядке.

20. Создать целый массив {x_i}, i = 1...n, состоящий из чисел Фибоначчи. Числа Фибоначчи вычисляются по формуле: a₀=a₁=1; a_n=a_n-1+a_n-2.

21. Заданы n материальных точек на плоскости. Каждая точка характеризуется массой m и 2 координатами: x и y. Найти центр "тяжести" этих точек. Расчетные формулы:

x_ц = Σx_i m_i / Σx_i y_ц = Σy_i m_i /y_i, i = 1...n.

22. Дана матрица {a_ij}, i =1...n, j = 1...n. Поменять местами элементы строки k с элементами столбца m, сохраняя прежний порядок их следования.

23. Дан упорядоченный по возрастанию значений элементов массив: {x_i}, i = 1...n и дано произвольное значение b. Вставить это значение в массив так, чтобы не нарушилась упорядоченность.

24. Дан массив: {x_i}, i = 1...n. Преобразовать массив {x_i}, i = 1...n-1 исключением из него минимального элемента массива с сохранением порядка следования остальных элементов массива x.

25. Известны координаты на плоскости n вершин ломаной линии, заданные в порядке обхода. Определить ее длину.

26. Дан массив: {x_i}, i = 1...n. Найти возрастающую подпоследовательность наибольшей длины.

27. Дано натуральное число. Выяснить, равен ли квадрат числа сумме его цифр.

28. Дано натуральное число. Является ли оно палиндромом? Примеры палиндромов: 2222, 6116, 0440 и т.д.

29. Клиент вносит в банк ежемесячно некоторые суммы(значение вводится с клавиатуры). Ежеквартально начисляются n процентов на сумму счета. Сколько будет на счете в начале следующего года, если в начале текущего эта сумма составляла N рублей. Клиент вносит в банк ежемесячно некоторые суммы(значение вводится с клавиатуры). Ежеквартально начисляются n процентов на сумму счета. Сколько будет на счете в начале следующего года, если в начале текущего эта сумма составляла N рублей.