(ПГС02 2016) Основы расчета строительных конструкций. Основные понятия курса. Цели и задачи курса. Состав, строение, состояние и физические свойства грунтов
 Скачать 1.65 Mb.
|
|
Раздел 3. Определение напряжений в массивах грунтов. Введение. Напряжения в массивах грунтов, служащих основанием, средой или материалом для сооружения, возникают под воздействием внешних нагрузок и собственного веса грунта. Основные задачи расчета напряжений: - распределение напряжений по подошве фундаментов и сооружений, а также по поверхности взаимодействия конструкций с массивами грунта, часто называемых контактными напряжениями; - распределение напряжений в массиве грунта от действия местной нагрузки, соответствующей контактным напряжениям; - распределение напряжений в массиве грунта от действия собственного веса, часто называемых природным давлением. 3.1. Определение контактных напряжений по подошве сооружения. При взаимодействии фундаментов и сооружений с грунтами основания на поверхности контакта возникают контактные напряжения. Характер распределения контактных напряжений зависит от жесткости, формы и размеров фундамента или сооружения и от жесткости (податливости) грунтов основания. 3.1.1. Классификация фундаментов и сооружений по жесткости. Различают три случая, отражающие способность сооружения и основания к совместной деформации: - абсолютно жесткие сооружения, когда деформируемость сооружения ничтожно мала по сравнению с деформируемостью основания и при определении контактных напряжений сооружение можно рассматривать как недеформируемое; - абсолютно гибкие сооружения, когда деформируемость сооружения настолько велика, что оно свободно следует за деформациями основания; - сооружения конечной жесткости, когда деформируемость сооружения соизмерима с деформируемостью основания; в этом случае они деформируются совместно, что вызывает перераспределение контактных напряжений. Критерием оценки жесткости сооружения может служить показатель гибкости по М. И. Горбунову-Посадову
где  и  - модули деформации грунта основания и материала конструкции;  и  – длина и толщина конструкции.3.1.2. Модель местных упругих деформаций и упругого полупространства. При определении контактных напряжений важную роль играет выбор расчетной модели основания и метода решения контактной задачи. Наибольшее распространение в инженерной практике получили следующие модели основания: - модель упругих деформаций; - модель упругого полупространства. 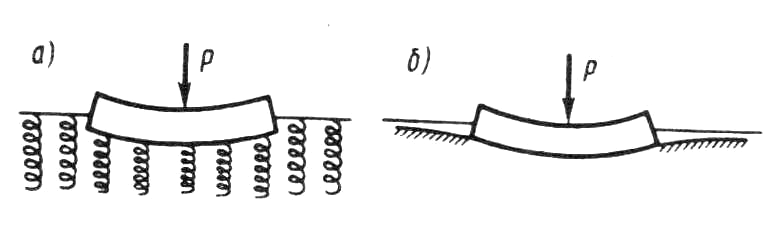 Рис. 3.1. Деформации поверхности основания: а – по модели местных упругих деформаций; б – по модели упругого полупространства Модель местных упругих деформаций. Согласно этой модели, реактивное напряжение в каждой точке поверхности контакта прямо пропорционально осадке поверхности основания в той же точке, а осадки поверхности основания за пределами габаритов фундамента отсутствуют (рис. 3.1.а.):
где  – коэффициент пропорциональности¸ часто называемый коэффициентом постели, Па/м.Модель упругого полупространства. В этом случае поверхность грунта оседает как в пределах площади загрузки, так и за её пределами, причём кривизна прогиба зависит от механических свойств грунтов и мощности сжимаемой толщи в основании (рис. 3.1.б.):
где  - коэффициент жесткости основания,  – координата точки поверхности, в которой определяется осадка;  - координата точки приложения силы  ;  – постоянная интегрирования.3.1.3. Влияние жесткости фундаментов на распределение контактных напряжений. Теоретически эпюра контактных напряжений под жестким фундаментом имеет седлообразный вид с бесконечно большими значениями напряжений по краям. Однако вследствие пластических деформаций грунта в действительности контактные напряжения характеризуется более пологой кривой и у края фундамента достигает значений, соответствующих предельной несущей способности грунта (пунктирная кривая на рис. 3.2.а.) 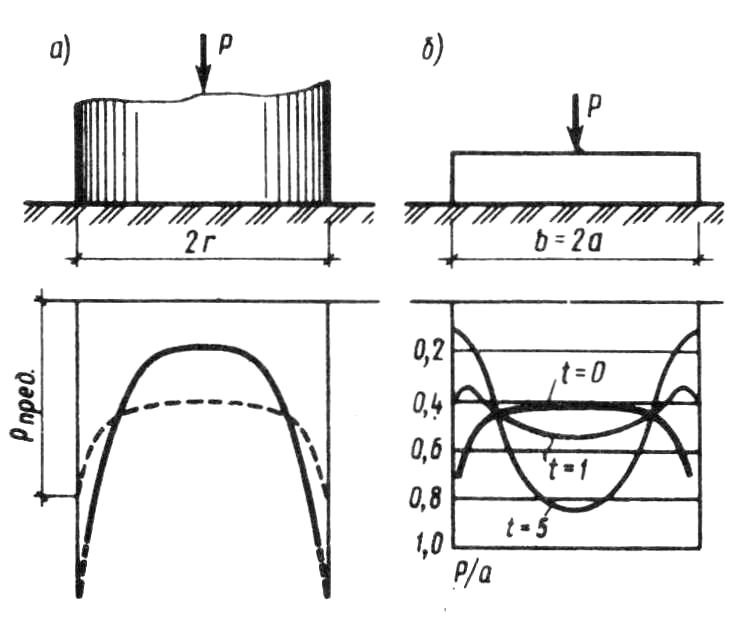 Рис.3.2. Эпюры контактных напряжений: а – под жестким круглым штампом; б – под плоским фундаментом при различном показателе гибкости Изменение показателя гибкости существенно сказывается на изменении характера эпюры контактных напряжений. На рис. 3.2.б. приведены контактные эпюры для случая плоской задачи при изменении показателя гибкости t от 0 (абсолютно жесткий фундамент) до 5. 3.2. Распределение напряжений в грунтовых основаниях от собственного веса грунта. Вертикальные напряжения от собственного веса грунта на глубине z от поверхности определяются формулой:
а эпюра природных напряжений будет иметь вид треугольника (рис. 3.3.а) При неоднородном напластовании с горизонтальным залеганием слоев эта эпюра будет уже ограничиваться ломаной линией Оабв, где наклон каждого отрезка в пределах мощности слоя 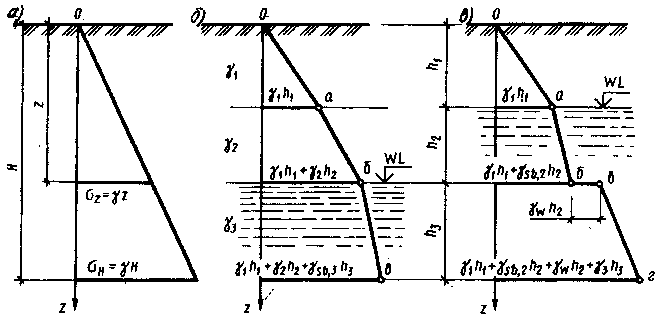 определяется значением удельного веса грунта этого слоя  (рис. 3.3.б). Рис.3.3. Характер распределения напряжений по оси фундамента в зависимости от формы и площади его подошвы Неоднородность напластования может вызываться не только наличием слоев с разными характеристиками, но и наличием в пределах толщи грунта уровня подземных вод (WL на рис. 3.3.в). В этом случае следует учесть уменьшение удельного веса грунта за счет взвешивающего действия воды на минеральные частицы:
где  - удельный вес грунта во взвешенном состоянии;  - удельный вес частиц грунта;  - удельный вес воды, принимаемый равным 10 кН/м3;  – коэффициент пористости грунта.3.2.0. Определение напряжений в грунтовом массиве от действия местной нагрузки на его поверхности. Распределение напряжений в основании зависит от формы фундамента в плане. В строительстве наибольшее распространение получили ленточные, прямоугольные и круглые фундаменты. Таким образом, основное практическое значение имеет расчет напряжений для случаев плоской, пространственной и осесимметричной задач. Напряжения в основании определяется методами теории упругости. Основание при этом рассматривается как упругое полупространство, бесконечно простирающееся во все стороны от горизонтальной поверхности загружения. 3.2.1. Задача о действии вертикальной сосредоточенной силы. Решение задачи о действии вертикальной сосредоточенной силы, приложенной к поверхности упругого полупространства полученное в 1885 г. Ж. Буссинеском, позволяет определить все компоненты напряжений и деформаций в любой точке полупространства 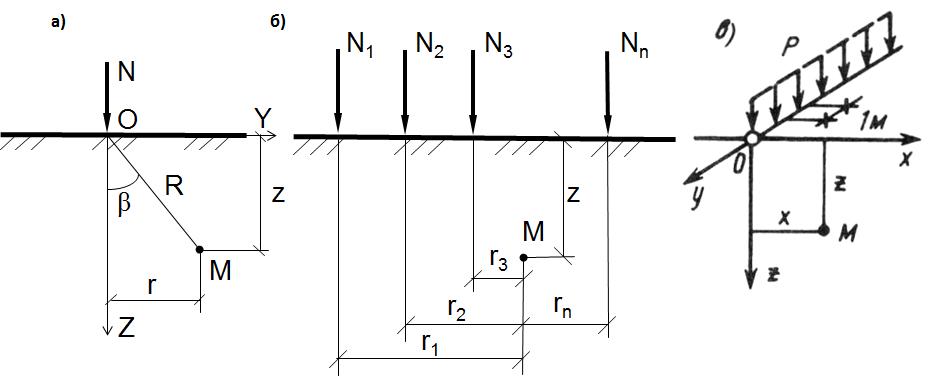 от действия силы (рис. 3.4.а). Рис. 3.4. Расчетные схемы основных задач: а – задача Буссинеска; б – задача о действии нескольких сил; в – задача Фламана Вертикальные напряжения определяются по формуле:
Используя принцип суперпозиции можно определить значение вертикального сжимающего напряжения в точке при действии нескольких сосредоточенных сил, приложенных на поверхности (рис. 3.4.б):
В 1892 г. Фламан получил решение для вертикальной сосредоточенной силы в условиях плоской задачи (рис. 3.4.в):
Зная закон распределения нагрузки на поверхности в пределах контура загружения, можно, интегрируя выражение (3.6) в пределах этого контура, определить значения напряжений в любой точке основания для случая осесимметричной и пространственной нагрузки (рис. 3.5.), а интегрируя выражение (3.8) – для случая плоской нагрузки. 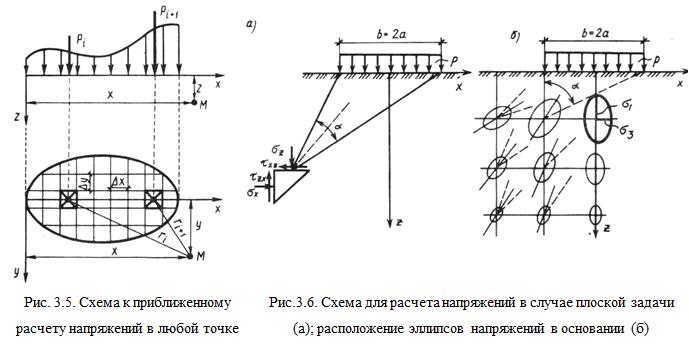 3.2.2. Плоская задача. Действие равномерно распределенной нагрузки. Схема для расчета напряжений в основании в случае плоской задачи при действии равномерно распределенной нагрузки интенсивностью  показана на рис. 3.6.а.Точные выражения для определения компонент напряжений в любой точке упругого полупространства были получены Г. В. Колосовым в виде:
где  ,  ,  - коэффициенты влияния, зависящие от безразмерных параметров  и  ; и  – координатные точки, в которой определяются напряжения;  – ширина полосы загружения.На рис. 3.7. а-в показано в виде изолиний распределение нарпряжении 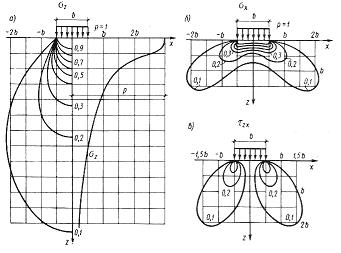 ,  и  в массиве грунте для случая плоской задачи. Рис.3.7. Изолинии напряжений для случая плоской задачи и эпюра вертикальных сжимающих напряжений по оси полосы загружения В некоторых случаях при анализе напряженного состояния основания оказывается удобнее пользоваться главными напряжениями. Тогда значения главных напряжений в любой точке упругого полупространства под действием полосовой равномерно распределенной нагрузки можно определить по формулам И. Х. Митчелла:
где  - угол видимости, образованный лучами, выходящими из данной точки к краям загруженной полосы (рис.3.6.б).3.2.3. Пространственная задача. Действие равномерно распределенной нагрузки. В 1935 г. А. Лявом были получены значения вертикальных сжимающих напряжений  в любой точке основания от действия нагрузки интенсивностью , равномерно распределенной по площади прямоугольника размером  .Практический интерес представляют компоненты напряжений 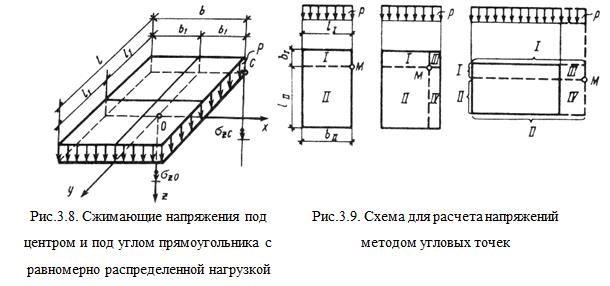 , относящиеся к вертикали, проведенной через угловую точку  этого прямоугольника, и  , действующие по вертикали, проходящей через его центр (рис. 3.8.). Используя коэффициенты влияния можно записать:
где -  и  - соответственно коэффициенты влияния для угловых и центральных напряжений, зависящие от соотношения сторон загруженного прямоугольника и относительной глубины точки, в которой определяются напряжения.Между значениями и имеется определенное соотношение.
Тогда оказывается удобным выразить формулы (3.11) через общий коэффициент влияния и записать их в виде:
Коэффициент зависит от безразмерных параметров  и  :  ,  (при определении углового напряжения ),  (при определении напряжения под центром прямоугольника ).3.2.4. Метод угловых точек. Метод угловых точек позволяют определить сжимающие напряжения в основании по вертикали, проходящей через любую точку поверхности. Возможны три варианта решения (рис.3.9.). Пусть вертикаль проходит через точку , лежащую на контуре прямоугольника. Разделив этот прямоугольник на два так, чтобы точка М являлась угловой для каждого из них, можно представить напряжения  как сумму угловых напряжений I и II прямоугольников, т.е.
Если точка лежит внутри контура прямоугольника, то его следует разделить на четыре части так, чтобы эта точка являлась угловой для каждого составляющего прямоугольника. Тогда:
Наконец, если точка лежит вне контура загруженного прямоугольника, то его нужно достроить так, чтобы эта точка вновь оказалась угловой.
3.2.5. Влияние формы и площади фундамента в плане. На рис. 3.10. построены эпюры нормальных напряжений 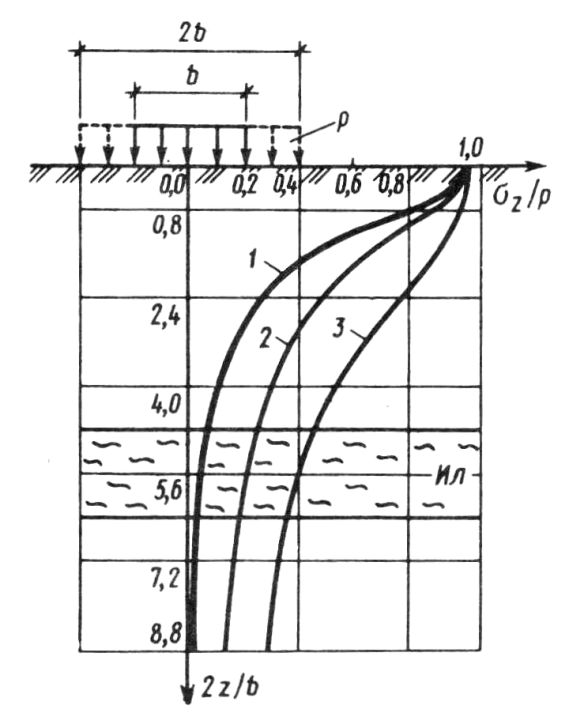 по вертикальной оси, проходящей через центр квадратного фундамента при  (кривая 1), ленточного фундамента  (кривая 2), и тоже, шириной  (кривая 3). Рис. 3.10. Характер распределения напряжений по оси фундамента в зависимости от формы и площади его подошвыВ случае пространственной задачи (кривая 1) напряжения с глубиной затухают значительно быстрее, чем для плоской задачи (кривая 2). Увеличение ширины, а, следовательно, и площади фундамента (кривая 3) приводит к ещё более медленному затуханию напряжений с глубиной. |
, где 
; 
; 
, где 
; 
; 
; 
,
; 
