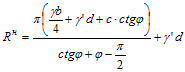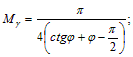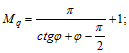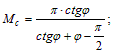(ПГС02 2016) Основы расчета строительных конструкций. Основные понятия курса. Цели и задачи курса. Состав, строение, состояние и физические свойства грунтов
 Скачать 1.65 Mb.
|
|
Раздел 4. Прочность и устойчивость грунтовых массивов. Давление грунтов на ограждения. Введение. При определенных условиях может происходить потеря устойчивости части грунтового массива, сопровождающаяся разрушением взаимодействующих с ней сооружений. Это связано с формированием в массиве некоторых областей, где соотношение между действующими напряжениями становится таким, что прочность грунта оказывается исчерпанной. Оценка устойчивости массива грунтов основывается на анализе напряжений, возникающих в них от собственного веса и проектируемого сооружения, и сопоставлений с предельными их значениями. Условие предельного равновесия в точке грунтового массива, характеризуются следующими выражениями теории предельного равновесия:
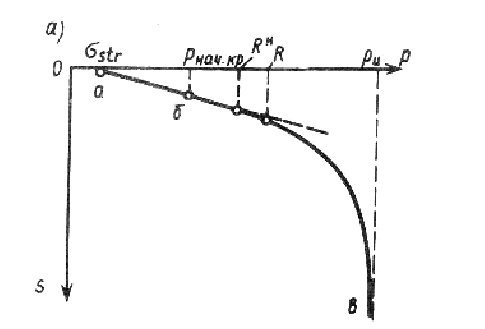
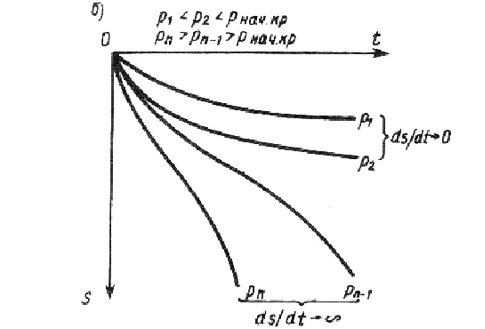
Эти выражения позволяют дать оценку напряженного состояния грунта, т.е. установить, находится ли грунт в до предельном или предельном состоянии, а, следовательно, на сколько устойчив массив. Предельное состояние грунта соответствует точке в рис. 4.1а, где осадка S уходит в бесконечность, т.о. теория предельного равновесия исследует только напряженное состояние массива грунтов и не дает возможности определить развивающиеся в нем деформации. 4.1. Критические нагрузки на грунты основания. Фазы напряженного состояния грунтовых оснований. (страница 1 из 4) Рассмотрим график зависимости  на рис. 4.1, а.Для связного грунта начальный участок графика Оа будет почти горизонтальным, протяженность этого участка определится величиной  структурной прочности грунт, а деформация имеет упругий характер. При увеличении давления (участок аб) осадка возрастает, развивается процесс уплотнения за счёт уменьшения пористости грунта. Зависимость  близка к линейной, осадки стремятся к постоянной величине (4.1, б).
Ни в одной точке основания не формируется предельное состояние. Наибольшее напряжение, ограничивающее этот участок, называется начальной критической нагрузкой pнач кр., а изменение нагрузки от 0 до pнач кр. характеризует фазу уплотнения грунта. При изменении давления под подошвой фундамента от 0 до pнач кр. ни в одной точке основания не возникает предельное состояние, т.е. происходит только уплотнение грунта, что абсолютно безопасно для основания.
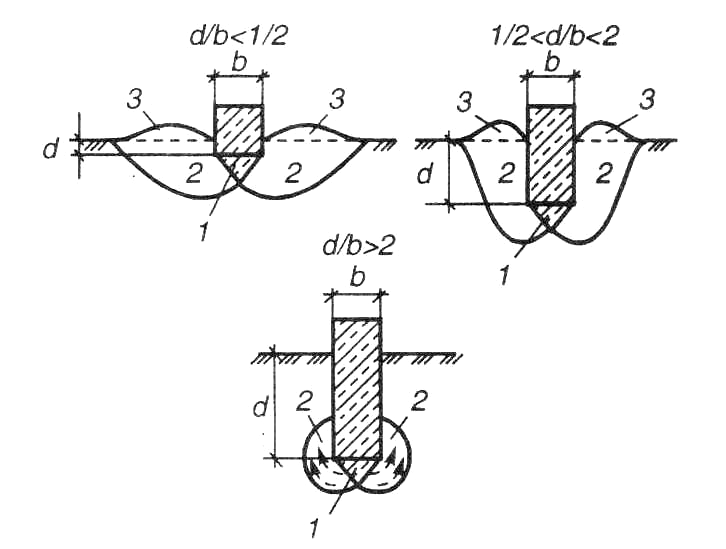
При дальнейшем увеличении нагрузки (участок бв рис.4.1, а) в точках, расположенных под краями фундамента, касательные напряжения по некоторым площадкам становятся равными их предельным значениям. По мере возрастания нагрузки эти точки объединяются в зоны, размеры которых увеличиваются. Возникают сдвиговые деформации, имеющие пластический характер. График зависимости всё больше отклоняется от линейного. Участок бв называют фазой сдвигов. Концу этой фазы соответствует ри, называемая предельной критической нагрузкой, при которой в основании образуются замкнутые области предельного равновесия, и происходит потеря устойчивости грунтов, т.е. полное исчерпание несущей способности.В зависимости от глубины заложения подошвы фундамента d/b очертания областей предельного равновесия имеют различный характер (рис. 4.2). Нагрузки, соответствующие pнач pкр. и ри называют критическими нагрузками, их определяют методами теории предельного равновесия. 4.1.1. Начальная критическая нагрузка. Начальная критическая нагрузка соответствует случаю, когда в основании под подошвой фундамента в единственной точке под гранью фундамента возникает предельное состояние. Выберем в основании точку М (рис. 4.3) и определим такое контактное напряжение р, при котором в этой точке возникнет предельное напряженное состояние. В модели линейно-деформируемой среды полные напряжения в точке М определятся как
где α – угол видимости. Предельное напряженное состояние в точке М реализуется при соблюдении условия (4.2). Подставив (4.3) в (4.2) получим:
Запишем соотношение для глубины самой нижней точки, в которой возможно предельное состояние от подошвы фундамента.
Решая это уравнение относительно p:
По определению при pнач.кр zmax=0. Тогда в единственной точке основания под гранью фундамента будет выполняться условие предельного равновесия:
Фундамент, спроектированный так, что напряжение под его подошвой не превышает начальной критической нагрузки (p нач.кр.), будет находиться в совершенно безопасном состоянии. Однако, как показала практика, грунты основания при этом будут обладать значительным резервом несущей способности. 4.1.2. Нормативное сопротивление и расчетное давление. Если допустить под подошвой центрально нагруженного фундамента шириной b развитие зон предельного равновесия на глубину  , то несущая способность основания остается обеспеченной. При этом осадки во времени затухают и стремятся к постоянной величине, а зависимость оказывается достаточно близкой к линейной. Следовательно, при этих условиях для расчётов деформации основания можно использовать формулы теории линейного деформирования грунтов.Нормативное сопротивление грунта основания Rн соответствует наибольшему среднему сжимающему напряжению под подошвой фундамента при котором по подошве фундамента допускается развития областей предельного состояния на глубину равную b/4.
Одним из основных условий определения размеров фундаментов является требование  , гдер – расчетное давление под подошвой фундамента.Выражение (4.8) часто представляют в виде трехчленной формулы:
здесь Mγ, Mq, Mc – некоторые функции от угла φ.
Значения этих коэффициентов приведены в СП 22.13330.2016 «Основания зданий и сооружений.» Актуализированная редакция СНиП 2.02.01-83*. Дальнейшие исследования позволили еще дальше отодвинуть практический предел среднего напряжения под подошвой фундамента, где так же допустим расчет осадок с учетом линейной деформации грунтов оснований. Эта величина, согласно СП 22.13330.2016, получила название расчетного сопротивления грунта R (4.11). В этом случае формула (4.9) имеет несколько более сложный вид (учет подвальных помещений, учет неоднородности грунта и т.п.) и будет рассмотрена в курсе «Основания и фундаменты».
4.1.3. Предельная критическая нагрузка. Предельная критическая нагрузка ри соответствует напряжению под подошвой фундамента, при котором происходит исчерпание несущей способности грунтов основания (рис. 4.1), что приводит к выдавливанию грунта из под фундамента и его огромнейшей осадке (рис. 4.2). Нагрузка, соответствующая ри приводит к полной потере устойчивости грунта основания и является абсолютно недопустимой для проектируемого сооружения. Решением этой задачи занимались Л.Прандль, К.Терцачи, В.В.Соколовский, М.В.Малышев. На рис. 4.3. представлена одна (левая) область предельного равновесия и два «семейства» линий скольжении, которые образуют ромбы скольжения с определенными углами наклона линий. 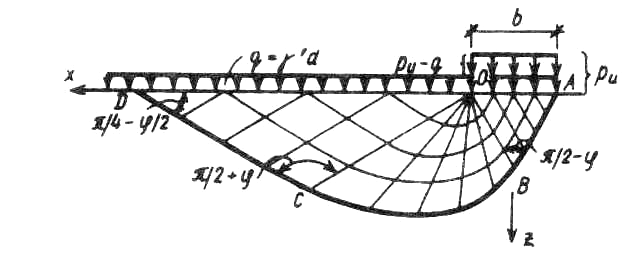 Рис.4.3. Линии скольжения при предельной полосовой нагрузке для невесомого основания (  =0)Наиболее полное решение этой задачи получено в 1952 году В.В.Соколовским.
где Nγ, Nq, N c= f(φ, δ) – затабулированные безразмерные коэффициенты. Приведенные выше решения справедливы при относительно небольших глубинах заложения фундаментов и однородном строении основания, поэтому в практических расчетах обычно используют инженерные способы, в той или иной мере учитывающие строгие решения теории предельного равновесия. 4.2. Практические способы расчета несущей способности и устойчивости оснований. Принципы расчета оснований фундаментов по I предельному состоянию (по прочности и несущей способности грунтов). Согласно СП 22.13330.2016 несущая способность основания считается обеспеченной при выполнении условия:
где: F – равнодействующая расчетной силы (нагрузки), приложенной к основанию; Fu – сила предельного сопротивления (равнодействующая предельной нагрузки); γс – коэффициент условий работы, зависящий от вида грунта. γn – коэффициент надежности по назначению сооружения. 4.3. Устойчивость откосов и склонов. Откосом называется искусственно созданная поверхность, ограничивающая природный грунтовый массив, выемку или насыпь. Откосы образуются при возведении различного рода насыпей (дамбы, земляные плотины и т.д.) и выемок (котлованы, траншеи, каналы и т.п.). Склоном называется откос, образованный природным путём и ограничивающий массив грунта естественного сложения. Основными причинами потери устойчивости откосов и склонов являются: - устройство недопустимо крутого откоса или подрезка склона, находящегося в состоянии, близком к предельному; - увеличение внешней нагрузки (возведение сооружений, складирование материалов на откос или вблизи его бровки); - изменение внутренних сил (изменение удельного веса грунта при изменении его влажности); - неправильное назначение расчетных характеристик прочности грунта или снижение его сопротивления сдвигу за счёт повышения влажности и др. причин; - проявление гидродинамического давления, сейсмических сил, различного рода динамических воздействий (движение транспорта, забивка свай и т.п.). 4.3.1. Понятие о коэффициенте запаса устойчивости откосов и склонов. Коэффициент устойчивости часто принимается в виде:
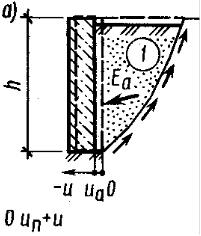
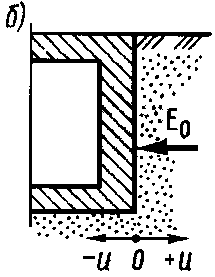
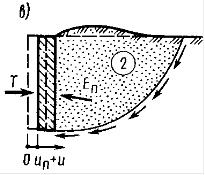
где φ, с – расчетные значения характеристик сопротивления сдвигу грунта, принятые в проекте; φ’, с’ – то же, соответствующие предельному состоянию откоса или склона. Устойчивость откоса или склона считается обеспеченной, если,  где  =1,1…1,3 - нормативный коэффициент устойчивости.Группы методов используемых для расчетов устойчивости склонов и откосов: - элементарные решения; - строгие решения; - инженерные методы; - численные методы. При этом анализируются два типа задач: 1). Оценка устойчивости откоса или склона заданной крутизны 2). Определение оптимальной крутизны откоса или склона при заданном .4.4. Простейшие методы расчетов устойчивости. 4.4.1. Устойчивость откосов в идеально сыпучих грунтах (ϕ ≠0; с=0). Имеется откос с углом заложения α, при заданном φ для песка, слагающего откос (рис.4.4, а). Рассмотрим равновесие частицы, свободно лежащей на поверхности откоса: т.к. грунт обладает только внутренним трением, то устойчивость будет обеспечена, если T≤T’. Задавшись весом частицы P и учитывая, что коэффициент 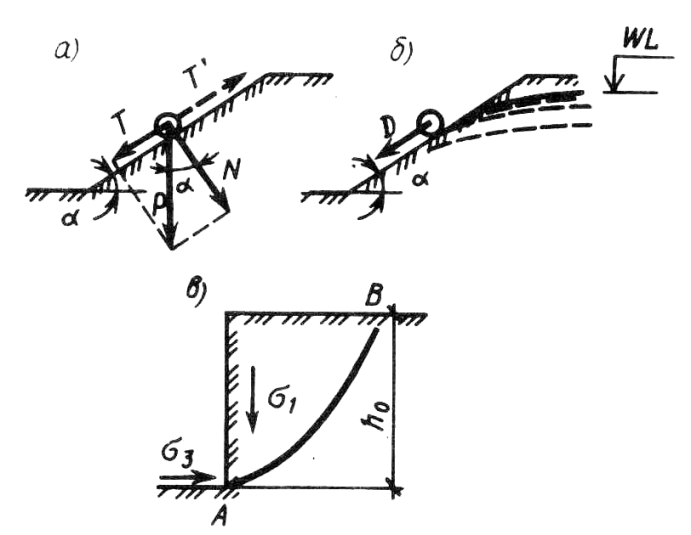 Рис.4.4. Схемы к расчету устойчивости откосов: а – идеально сыпучего грунта; б – то же, при действии фильтрационных сил; в – идеально связного грунта внутреннего трения грунтов  , получим; ;  , откуда  или  при α=φ в идеально сыпучих грунтах угол естественного откоса – α равен углу внутреннего трения грунта. Окончательно  при откос обладает необходимым запасом устойчивости.В случае, если требуется определить угол заложения будущего откоса с запасом устойчивости, то α соответственно определиться как:  4.4.2. Учет влияния фильтрационных сил. Если уровень подземных вод находится выше подошвы откоса, возникает фильтрационный поток, выходящий на его поверхность, что приводит к снижению устойчивости откоса. В этом случае при рассмотрении равновесия частицы необходимо добавить гидродинамическую составляющую D. Гидравлический градиент в точке выхода потока равен:  , а гидравлическая составляющая в единице объема грунта равна: γw – удельный вес воды; n – пористость. Учитывая, что вес единицы объема грунта P=γV, где V=1. Уравнение предельного состояния запишется как:  т.к.  , после преобразования получим  Угол заложения откоса при заданном нормативном коэффициенте устойчивости: 4.5. Инженерные методы расчёта устойчивости откосов и склонов. В проектной практике применяются инженерные методы, содержащие различные упрощения. 4.5.1. Метод круглоцилиндрических поверхностей скольжения. Предполагается, что потеря устойчивости откоса (склона) может произойти в результате вращения отсека грунтового массива относительно некоторого центра О(рис. 4.5, а). 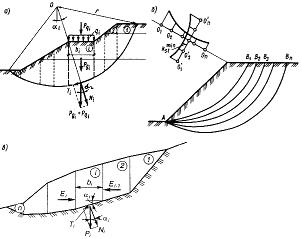 Рис.4.5. Схема к расчету устойчивости откосов методом круглоцилиндрический поверхностей скольжения: 1, 2, … - номера элементов Суть метода заключается в анализе устойчивости склона против сдвига по ряду возможных поверхностей скольжения, представленных дугой окружности с радиусомr и центром в т. О. Отсек грунтового массива, ограниченный свободной поверхностью и поверхностью скольжения, разбивается вертикальными линиями на nэлементов таким образом, чтобы можно было принять основание каждого отсека плоским, а прочностные характеристики постоянными. Смещающийся массив рассматривается как недеформируемый отсек, все точки которого участвуют в общем движении. Коэффициент устойчивости принимается в виде:  , где Мsr и Msa – моменты относительно центра вращения О всех сил, соответственно удерживающих и смещающих отсек.Порядок вычислений: 1. Грунтовый массив разбивается на отдельные элементы. 2. Вычисляются вертикальные силы, действующие на каждый элемент: собственный вес грунта Pgi и равнодействующая нагрузки на его поверхности Pqi. 3. Равнодействующая сил Pgi+Pqi раскладывается на нормальную Ni и касательную Ti составляющие.  ;  .4. Находим c и li – длину дуги. Момент сил, вращающих отсек вокруг т. О, определится как:  .n – число элементов в отсеке. удерживающие силы обуславливаются сопротивлением сдвигу за счет внутреннего трения и сцепления грунта. Сила трения:  При наличии внешних вертикальных нагрузок они включаются в величину веса блока (призмы).  α – угол между нормалью к основанию i-го элемента и вертикалью.  - длина основания i-го элемента, где bi – ширина i-го отсека.φI i и cI i – расчетные значения характеристик прочности грунта в пределах основания i-го элемента.  Соотносительно: 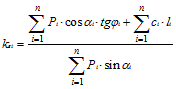 При kst ≥ kнst устойчивость откоса относительно выбранного центра вращения т.О обеспечена. - Основная сложность при практических расчетах заключается в том, что положение центра вращения О и выбор радиуса r, соотносящие наиболее опасному случаю, неизвестны. - Обычно проводится серия таких расчетов при различных положениях центров вращения и значениях r. - Чаще всего наиболее опасная поверхность скольжения проходит через нижнюю точку откоса (склона). Кроме слабых грунтов с минимальными φ и с. 4.5.2. Мероприятия по повышению устойчивости откосов и склонов. Одним из наиболее эффективных способов повышения устойчивости откосов и склонов является их выполаживание или создание уступчатого профиля с образованием горизонтальных площадок (берм) по высоте откоса. При относительно небольшой высоте откоса эффективна пригрузка подошвы в его низовой части или устройство подпорной стенки, поддерживающей откос. Закрепление поверхности откоса может быть осуществлено мощением камнем, одерновкой, укладкой бетонных плит. Важнейшим мероприятием является регулирование гидрогеологического режима откоса или склона. Устройство канав для перехватывания поверхностных вод, отвод воды с берм, устройство дренажа. Конструктивные мероприятия типа прорезания потенциально неустойчивого массива грунтов системой забивных или набивных свай, анкерное закрепление во взаимодействии с подпорными стенками или свайными конструкциями. 4.6. Понятия о взаимодействии грунтов с ограждающими конструкциями (давление покоя, активное и пассивное давление). Ограждающие конструкции предназначены для удерживания от обрушения находящихся за ними грунтовых массивов. К таким конструкциям относится подпорная стенка, а также стены подвалов и заглубленных частей здания, стены подземных сооружений и т.п. Различают массивные (или гравитационные) и тонкостенные подпорные стенки (рис. 4.6). По характеру работы подразделяются на жесткие и гибкие (шпунтовые стенки). 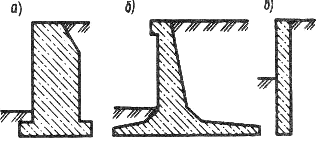 Рис.4.6. Примеры конструкций подпорных стенок: а – массивной; б – тонкостенной; в – то же, заделанной в основание Устойчивость массивных стенок на сдвиг и опрокидывание обеспечивается прежде всего их собственным весом. Устойчивость тонкостенных конструкций – собственным весом стенки и грунта, вовлеченного в совместную работу, либо защемлением нижней части стенки в основание. Равнодействующая давления грунта на стенку Е зависит от направления, величины и характера её смещения.
Рис.4.7 Связь равнодействующей давления грунта Е с величиной и направлением горизонтального смещения u стенки. Давление, реализуемое в условиях отсутствия горизонтального смещения при u=0 (рис. 4.7, б) называютдавлением покоя Е0.  ,где  - коэф. бокового давления; ν – коэф. Пуассона, γ – удельный вес грунта.При смещении стенки под действием давления в сторону от засыпки на величину ua (рис.4.7, а) в грунте засыпки формируется область обрушения грунта, граница которой называется поверхностью скольжения, а сама область – призмой обрушения. Давление, передаваемое призмой обрушения на грань стенки, называютактивным давлением, а его результирующую обозначают Еа. При смещении стенки в сторону грунта под действием каких-либо сил в засыпке также образуются поверхности скольжения, при величине смещения +uп формируется призма выпирания грунта (рис.4.7, в). При этом реакция грунта достигает максимального значения и соответствует пассивному давлению (отпору) грунта, результирующую которого обозначают Еп. 4.6.1. Определение активного давления на вертикальную грань стенки для сыпучего грунта и связного грунта, учёт пригрузки на поверхности засыпки. Трение грунта о стенку отсутствует (τzx=0). Максимальное главное напряжение, действующее на горизонтальную площадку в точке контакта грунта со стенкой на глубине z от поверхности засыпки 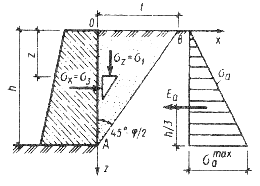 , γ – удельный вес грунта. Рис.4.8. Схема для определения активного давления сыпучего грунта на гладкую стенку Грунт в пределах призмы обрушения ОАВ (рис. 4.8) находится в состоянии предельного равновесия. Минимальное главное напряжение σ3, равное активному давлению σа, связано с максимальным главным напряжением условием предельного равновесия:   .Эпюра активного давления имеет вид треугольника. Максимальная ордината эпюры активного давления:  .Равнодействующая активного давленияЕа определяется как площадь эпюры   ,И будет приложена к стенке на расстоянии 1/3h от её подошвы. Плоскость скольжения АВ будет наклонена к вертикали под углом π/4-φ/2. Ширина призмы обрушения по поверхности засыпки l=htg(45°- φ/2). 4.6.2. Учёт пригрузки на поверхности засыпки. При наличии на поверхности сплошной равномерно распределенной нагрузки интенсивностью q:  . ; .Эпюра активного давления при наличии пригрузки на поверхности имеет вид трапеции. Точка приложения равнодействующей Ea будет находиться в центре тяжести площади трапеции. 4.6.3. Учёт сцепления грунта. Для связного грунта, обладающего внутренним трением и сцеплением:   Связный грунт обладает способностью держать вертикальный откос высотой h0  В пределах глубины h0 от свободной поверхности засыпки связный грунт не будет оказывать давления на стенку. Максимальная ордината эпюры активного давления связного грунта:  Учет сцепления грунта приводит к уменьшению активного давления. 4.6.4. Определение пассивного давления. Пассивное давление возникает при перемещении стенки в сторону грунта засыпки (рис. 4.9). 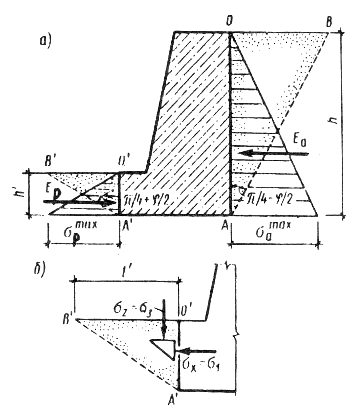 Рис.4.9. Схема действия активного и пассивного давления на стенку При движении вертикальной гладкой стенки на грунт главные напряжения меняются. Теперь уже σx=σ1= σп является максимальным, а σz=σ3=γz при отсутствии пригрузки на поверхности засыпки слева – минимальным главным напряжением (рис. 4.9, б). Условие предельного равновесия имеет вид: - для сыпучих грунтов:  - для связных грунтов:  Значения ординаты пассивного давления на глубине z от поверхности засыпки при начале координат в точке 0’: - для сыпучих грунтов:  - для связных грунтов:  При одной и той же глубине от поверхности засыпки ордината эпюры пассивного давления существенно больше, чем ордината эпюры активного давления. Ширина призмы выпирания l’=htg(45°+ φ/2). | |||||||||||||||||||||||||||||||||||||||||||||||||||||
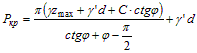
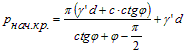- формула Пузыревского
,
;
,
