Основные понятия математической логики

• Название: Основные понятия математической логики
• Дата: 16.02.2022
• Размер: 2.32 Mb.
• Имя файла: ege15.doc
• Тип: Закон; #363571
• страница: 5 из 50

Ещё пример задания:

Р-28. На числовой прямой даны отрезки A = [70; 90], B = [40; 60] и C = [0; N] и функция

F(x) = ( (x  A)  (x  B) )  ( (x  C)  (x  A) )

При каком наименьшем числе N функция F(x) истинна более чем для 30 целых чисел x?

Решение:

1. 
   для сокращения записи введём обозначения
   

A = (xA), B = (xB), C = (xC).

фактически A(x) – это логическая функция, определяющая принадлежность числа x отрезку A

2. 
   запишем функцию в виде:
   

3. 
   используя распределительный закон логики, упрощаем:
   

4. 
   это значит, что функция истинна на всём отрезке A (там 21 целое число) и на общей части отрезков B и C, где должно быть не менее 31 – 21 = 10 целых чисел
   
5. 
   нарисуем отрезки на числовой оси: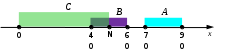
   

6. 
   по рисунку видно, что
   

1. 
   при N < 40 отрезки B и Cне имеют общей части
   
2. 
   при N  [40; 60] общая части отрезков B и C– это отрезок [40; N], на нём расположены
   N – 40 + 1 целых чисел
   
3. 
   при N > 60 общая части отрезков B и C совпадает с отрезком B, ему принадлежит 21 целое число
   

7. 
   таким образом, функция F(x) может быть истинной не более чем для 42 целых чисел
   
8. 
   если требуется обеспечить её истинность для 31 целого числа, нужно выбрать N из условия
   

N – 40 + 1 = 10, откуда N = 49

9. 
   Ответ: 49.
   

Решение (программа на Python, А.Н. Носкин):

1. 
   Упрощаем выражение:
   
2. 
   Примем отрезки за множество, тогда все числа отрезков будут элементами соответствующего множества. Сумма количества элементов множества А и количества элементов, которые соответствуют пересечению множеств В и С должна быть более 30.
   
3. 
   Создадим множества А, В и С:
   

A = {i for i in range(70,91)} #множество A

B = {i for i in range(40,61)} # множество B

C = set() #множество C

4. 
   В цикле будем добавлять элементы в множество С, пока сумма элементов А + В*С не достигнет более 30.
   

for N in range(90):

C.add(N)

Если такое число достигнуто, то выводим ответ:

if (len(A)+ len(B&C))>30:

print(N)

break

5. 
   Приведем полную программу:
   

A = {i for i in range(70,91)} # множество A

B = {i for i in range(40,61)} # множество B

C = set() #множество C

for N in range(90):

C.add(N)

if (len(A)+ len(B&C))>30:

print(N)

break

6. 
   Ответ: 49.
   

Решение (программа на Python, Е. Джобс):

1. 
   Полный текст программы:
   

# перебираем заведомо больший диапазон чисел

for N in range(10000):

# если в диапазоне [0; 1000] больше 30 удовлетворяющих чисел

if sum(

((not (70 <= x <= 90)) <= (40 <= x <= 60) ) and

((not (0 <= x <= N)) <= (70 <= x <= 90))

for x in range(1000)

) > 30:

print(N) # печатаем N

break # завершаем алгоритм

2. 
   Ответ: 49.