Ррр. Основные понятия математической логики

• Название: Основные понятия математической логики
• Дата: 03.10.2022
• Размер: 2.23 Mb.
• Имя файла: ege15.doc
• Тип: Закон; #710566
• страница: 14 из 48

Ещё пример задания:

Р-16. Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m». Для какого наибольшего натурального числа А формула

¬ДЕЛ(x, А)  (ДЕЛ(x, 6)  ¬ДЕЛ(x, 4))

тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х)?

Решение:

1. 
   введём обозначения A = ДЕЛ(x, А), P = ДЕЛ(x, 6) и Q = ДЕЛ(x, 4)
   
2. 
   введём множества:
   

A –множество натуральных чисел, для которых выполняется условие A

P –множество натуральных чисел, для которых выполняется условие P

Q –множество натуральных чисел, для которых выполняется условие Q

3. 
   истинным для всех X должно быть выражение
   

4. 
   упростим это выражение, раскрыв импликацию по правилу :
   

5. 
   из этой формулы видно, что множество A должно перекрыть множество, которое не перекрыто множеством , то есть перекрыть множество
   
6. 
   множество – это множество всех чисел, которые делятся одновременно на 4 и 6 (все числа, кратные 4 и 6), то есть, 12, 24, 36 и т.д. (заметим, что 12 – это наименьшее общее кратное чисел 4 и 6)
   
7. 
   для того, чтобы перекрыть эти числа, можно выбрать в качестве A любой делитель числа 12, то есть, 1, 2, 3, 4, 6 или 12; наибольшее из этих чисел – 12.
   
8. 
   Ответ: 12.
   

Ещё пример задания:

Р-15. На числовой прямой даны два отрезка: P = [5; 30] и Q = [14;23]. Укажите наибольшую возможную длину такого отрезка A, что формула



тождественно истинна, то есть принимает значение 1 при любом значении переменной х.

Решение:

1. 
   Для того чтобы упростить понимание выражения, обозначим отдельные высказывания буквами
   

A: x  А, P: x  P, Q: x  Q

2. 
   перейдем к более простым обозначениям
   

3. 
   раскрываем импликацию по формуле :
   

4. 
   поскольку это выражение должно быть равно 1, то должно быть истинным (и, следовательно, – ложным!) везде, где ложно ;
   
5. 
   таким образом, может быть истинным только там, где истинно
   
6. 
   выражение 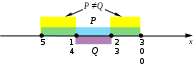истинно на двух интервалах: [5; 14) и (23; 30], которые входят в и не входят в , на рисунке они обозначены жёлтым цветом:
   

7. 
   значение может быть истинным только внутри этих полуинтервалов, выделенных желтым цветом; но поскольку – это отрезок, его наибольшая длина – это длина наибольшего из «жёлтых» полуинтервалов, то есть, 14 – 5 = 9 (длина второго полуинтервала равна 30 – 23 = 7).
   
8. 
   Ответ: 9.